
T4题意表述不清,理解错了
6171. 和相等的子数组
给你一个下标从 0 开始的整数数组 nums ,判断是否存在 两个 长度为 2 的子数组且它们的 和 相等。注意,这两个子数组起始位置的下标必须 不相同 。
如果这样的子数组存在,请返回 true,否则返回 false 。
子数组 是一个数组中一段连续非空的元素组成的序列。
示例 1:
输入:nums = [4,2,4] 输出:true 解释:元素为 [4,2] 和 [2,4] 的子数组有相同的和 6 。
示例 2:
输入:nums = [1,2,3,4,5] 输出:false 解释:没有长度为 2 的两个子数组和相等。
示例 3:
输入:nums = [0,0,0] 输出:true 解释:子数组 [nums[0],nums[1]] 和 [nums[1],nums[2]] 的和相等,都为 0 。 注意即使子数组的元素相同,这两个子数组也视为不相同的子数组,因为它们在原数组中的起始位置不同。
提示:
- 2 <= nums.length <= 1000
- -109 <= nums[i] <= 109
思路:
哈希表
class Solution {public boolean findSubarrays(int[] nums) {Set<Integer> set = new HashSet<>();for (int i = 1; i < nums.length; i++) {int s = nums[i - 1] + nums[i];if (set.contains(s)) return true;set.add(s);}return false;}}
6172. 严格回文的数字
如果一个整数 n 在 b 进制下(b 为 2 到 n - 2 之间的所有整数)对应的字符串 全部 都是 回文的 ,那么我们称这个数 n 是 严格回文 的。
给你一个整数 n ,如果 n 是 严格回文 的,请返回 true ,否则返回_ _false 。
如果一个字符串从前往后读和从后往前读完全相同,那么这个字符串是 回文的 。
示例 1:
输入:n = 9 输出:false 解释:在 2 进制下:9 = 1001 ,是回文的。 在 3 进制下:9 = 100 ,不是回文的。 所以,9 不是严格回文数字,我们返回 false 。 注意在 4, 5, 6 和 7 进制下,n = 9 都不是回文的。
示例 2:
输入:n = 4 输出:false 解释:我们只考虑 2 进制:4 = 100 ,不是回文的。 所以我们返回 false 。
提示:
- 4 <= n <= 105
思路:
结论题 return false
比赛时模拟直接写的
class Solution {public boolean isStrictlyPalindromic(int n) {for (int x = 2; x <= n - 2; x++) {var s = parseInt(n, x);if (!check(s)) return false;}return true;}List<String> parseInt(int n, int base) {List<String> res = new ArrayList<>();while (n > 0) {res.add(n % base + "");n /= base;}return res;}boolean check(List<String> s) {int i = 0, j = s.size() - 1;while (i < j) {if (s.get(i).compareTo(s.get(j)) != 0)return false;i++;j--;}return true;}}
6173. 被列覆盖的最多行数
给你一个下标从 0 开始的 m x n 二进制矩阵 mat 和一个整数 cols ,表示你需要选出的列数。
如果一行中,所有的 1 都被你选中的列所覆盖,那么我们称这一行 被覆盖 了。
请你返回在选择 cols 列的情况下,被覆盖 的行数 最大 为多少。
示例 1: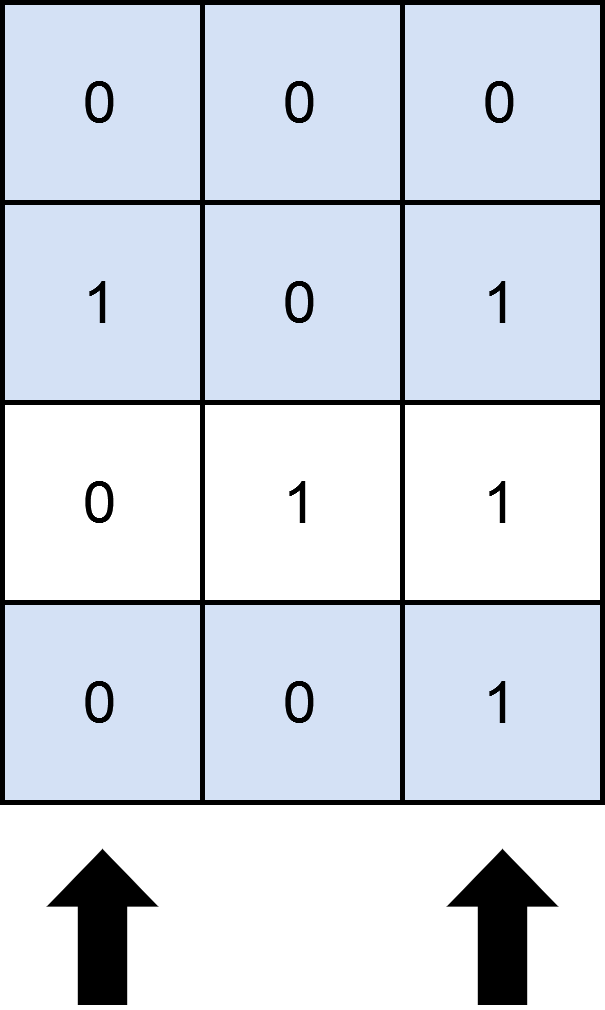
输入:mat = [[0,0,0],[1,0,1],[0,1,1],[0,0,1]], cols = 2 输出:3 解释: 如上图所示,覆盖 3 行的一种可行办法是选择第 0 和第 2 列。 可以看出,不存在大于 3 行被覆盖的方案,所以我们返回 3 。
示例 2:
输入:mat = [[1],[0]], cols = 1 输出:2 解释: 选择唯一的一列,两行都被覆盖了,原因是整个矩阵都被覆盖了。 所以我们返回 2 。
提示:
- m == mat.length
- n == mat[i].length
- 1 <= m, n <= 12
- mat[i][j] 要么是 0 要么是 1 。
- 1 <= cols <= n
思路:二进制枚举
class Solution {public int maximumRows(int[][] mat, int cols) {int n = mat.length, m = mat[0].length;int max = 0;for (int i = 0; i < 1 << m; i++) {if (Integer.bitCount(i) != cols) continue;int c = 0;for (int j = 0; j < n; j++) {boolean flag = true;for (int k = 0; k < m; k++) {if (mat[j][k] == 1 && (i >> k & 1) != 1) {flag = false;break;}}if (flag) c++;}max = Math.max(max, c);}return max;}}
6143. 预算内的最多机器人数目
你有 n 个机器人,给你两个下标从 0 开始的整数数组 chargeTimes 和 runningCosts ,两者长度都为 n 。第 i 个机器人充电时间为 chargeTimes[i] 单位时间,花费 runningCosts[i] 单位时间运行。再给你一个整数 budget 。
运行 k 个机器人 总开销 是 max(chargeTimes) + k sum(runningCosts) ,其中 max(chargeTimes) 是这 k 个机器人中最大充电时间,sum(runningCosts) 是这 k 个机器人的运行时间之和。
请你返回在 不超过 budget 的前提下,你 最多 可以 *连续 运行的机器人数目为多少。
示例 1:
输入:chargeTimes = [3,6,1,3,4], runningCosts = [2,1,3,4,5], budget = 25 输出:3 解释: 可以在 budget 以内运行所有单个机器人或者连续运行 2 个机器人。 选择前 3 个机器人,可以得到答案最大值 3 。总开销是 max(3,6,1) + 3 sum(2,1,3) = 6 + 3 6 = 24 ,小于 25 。 可以看出无法在 budget 以内连续运行超过 3 个机器人,所以我们返回 3 。
示例 2:
输入:chargeTimes = [11,12,19], runningCosts = [10,8,7], budget = 19 输出:0 解释:即使运行任何一个单个机器人,还是会超出 budget,所以我们返回 0 。
提示:
- chargeTimes.length == runningCosts.length == n
- 1 <= n <= 5 * 104
- 1 <= chargeTimes[i], runningCosts[i] <= 105
- 1 <= budget <= 1015
思路:
方法1:二分 + 单调队列
class Solution {public int maximumRobots(int[] e, int[] w, long budget) {int n = e.length;int[] q = new int[n];int hh = 0, tt = -1;int l = 0, r = n;while (l < r) {int mid = l + r + 1 >> 1;hh = 0;tt = -1;boolean flag = false;long s = 0;for (int i = 0; i < n; i++) {s += w[i];while (hh <= tt && e[q[tt]] <= e[i])tt--;q[++tt] = i;if (q[hh] <= i - mid)hh++;if (i - mid >= 0) s -= w[i - mid];if (i >= mid - 1 && s * mid <= budget - e[q[hh]]) {flag = true;break;}}if (flag) l = mid;else r = mid - 1;}return l;}}
方法2:双指针 + 单调队列
class Solution {public int maximumRobots(int[] e, int[] w, long budget) {int n = e.length;int[] q = new int[n];int hh = 0, tt = -1;long s = 0;int max = 0;for (int i = 0, j = 0; i < n; i++) {s += w[i];while (hh <= tt && e[q[tt]] <= e[i])tt--;q[++tt] = i;while (hh <= tt && s * (i - j + 1) + e[q[hh]] > budget) {if (q[hh] == j)hh++;s -= w[j];j++;}max = Math.max(max, i - j + 1);}return max;}}
拓展:
如果是子序列怎么办?见1383
在1383的基础上,不限制k,而是限制表现值,问需要的最小工程师数怎么办?
答:结合二分
1383. 最大的团队表现值
公司有编号为 1 到 n 的 n 个工程师,给你两个数组 speed 和 efficiency ,其中 speed[i] 和 efficiency[i] 分别代表第 i 位工程师的速度和效率。请你返回由最多 k 个工程师组成的 最大团队表现值 ,由于答案可能很大,请你返回结果对 10^9 + 7 取余后的结果。
团队表现值 的定义为:一个团队中「所有工程师速度的和」乘以他们「效率值中的最小值」。
示例 1:
输入:n = 6, speed = [2,10,3,1,5,8], efficiency = [5,4,3,9,7,2], k = 2 输出:60 解释: 我们选择工程师 2(speed=10 且 efficiency=4)和工程师 5(speed=5 且 efficiency=7)。他们的团队表现值为 performance = (10 + 5) min(4, 7) = 60 。
示例 2:
输入:n = 6, speed = [2,10,3,1,5,8], efficiency = [5,4,3,9,7,2], k = 3 输出:68 解释: 此示例与第一个示例相同,除了 k = 3 。我们可以选择工程师 1 ,工程师 2 和工程师 5 得到最大的团队表现值。表现值为 performance = (2 + 10 + 5) min(5, 4, 7) = 68 。
示例 3:
输入:n = 6, speed = [2,10,3,1,5,8], efficiency = [5,4,3,9,7,2], k = 4 输出:72
提示:
- 1 <= n <= 10^5
- speed.length == n
- efficiency.length == n
- 1 <= speed[i] <= 10^5
- 1 <= efficiency[i] <= 10^8
- 1 <= k <= n
思路:
排序 + 优先队列
class Solution {public int maxPerformance(int n, int[] speed, int[] efficiency, int k) {int[][] a = new int[n][2];for (int i = 0; i < n; i++) {a[i][0] = efficiency[i];a[i][1] = speed[i];}Arrays.sort(a, (o1, o2) -> (o2[0] - o1[0]));PriorityQueue<Integer> q = new PriorityQueue<>();long s = 0;long res = 0;for (int[] p : a) {int e = p[0], w = p[1];s += w;q.offer(w);if (q.size() > k) {s -= q.poll();}res = Math.max(res, s * e);}return (int)(res % (int)(1e9 + 7));}}

