image.png
又是3题的夜晚，注定睡不好觉

6051. 统计是给定字符串前缀的字符串数目

给你一个字符串数组 words 和一个字符串 s ，其中 words[i] 和 s 只包含 小写英文字母 。
请你返回 words 中是字符串 s 前缀 的 字符串数目 。
一个字符串的 前缀 是出现在字符串开头的子字符串。子字符串 是一个字符串中的连续一段字符序列。

示例 1：
输入：words = [“a”,”b”,”c”,”ab”,”bc”,”abc”], s = “abc” 输出：3 解释： words 中是 s = “abc” 前缀的字符串为： “a” ，”ab” 和 “abc” 。 所以 words 中是字符串 s 前缀的字符串数目为 3 。
示例 2：
输入：words = [“a”,”a”], s = “aa” 输出：2 解释： 两个字符串都是 s 的前缀。 注意，相同的字符串可能在 words 中出现多次，它们应该被计数多次。

提示：

  • 1 <= words.length <= 1000
  • 1 <= words[i].length, s.length <= 10
  • words[i] 和 s 只 包含小写英文字母。

思路：
API使用
时间复杂度: O(nm), n指words的长度，m指字符串长度

  1. class Solution {
  2.     public int countPrefixes(String[] words, String s) {
  3.         int cnt = 0;
  4.         for (String w : words) {
  5.             if (s.startsWith(w))
  6.                 cnt++;
  7.         }
  8.         return cnt;
  9.     }
  10. }

6052. 最小平均差

给你一个下标从 0 开始长度为 n 的整数数组 nums 。
下标 i 处的 平均差 指的是 nums 中 前 i + 1 个元素平均值和 后 n - i - 1 个元素平均值的 绝对差 。两个平均值都需要 向下取整 到最近的整数。
请你返回产生 最小平均差 的下标。如果有多个下标最小平均差相等，请你返回 最小 的一个下标。
注意：

  • 两个数的 绝对差 是两者差的绝对值。
  • n 个元素的平均值是 n 个元素之 和 除以（整数除法） n 。
  • 0 个元素的平均值视为 0 。

示例 1：
输入：nums = [2,5,3,9,5,3]
输出：3
解释：
- 下标 0 处的平均差为：|2 / 1 - (5 + 3 + 9 + 5 + 3) / 5| = |2 / 1 - 25 / 5| = |2 - 5| = 3 。
- 下标 1 处的平均差为：|(2 + 5) / 2 - (3 + 9 + 5 + 3) / 4| = |7 / 2 - 20 / 4| = |3 - 5| = 2 。
- 下标 2 处的平均差为：|(2 + 5 + 3) / 3 - (9 + 5 + 3) / 3| = |10 / 3 - 17 / 3| = |3 - 5| = 2 。
- 下标 3 处的平均差为：|(2 + 5 + 3 + 9) / 4 - (5 + 3) / 2| = |19 / 4 - 8 / 2| = |4 - 4| = 0 。
- 下标 4 处的平均差为：|(2 + 5 + 3 + 9 + 5) / 5 - 3 / 1| = |24 / 5 - 3 / 1| = |4 - 3| = 1 。
- 下标 5 处的平均差为：|(2 + 5 + 3 + 9 + 5 + 3) / 6 - 0| = |27 / 6 - 0| = |4 - 0| = 4 。
下标 3 处的平均差为最小平均差，所以返回 3 。
示例 2：
输入：nums = [0]
输出：0
解释： 唯一的下标是 0 ，所以我们返回 0 。 下标 0 处的平均差为：|0 / 1 - 0| = |0 - 0| = 0 。

提示：

  • 1 <= nums.length <= 105
  • 0 <= nums[i] <= 105

思路：
前缀和
时间复杂度：O(n)
空间复杂度：O(n)

  1. class Solution {
  2.     public int minimumAverageDifference(int[] nums) {
  3.         int n = nums.length;
  4.         long[] s = new long[n];
  6.         s[0] = nums[0];
  7.         for (int i = 1; i < n; i++)
  8.             s[i] = s[i - 1] + nums[i];
  10.         int min = 0x3f3f3f3f, idx = -1;
  12.         for (int i = 0; i < n; i++) {
  13.             long pre = s[i] / (i + 1);
  14.             long last = i == n - 1 ? 0 : (s[n - 1] - s[i]) / (n - i - 1);
  16.             int minus = (int)(Math.abs(pre - last));
  17.             if (minus < min) {
  18.                 min = minus;
  19.                 idx = i;
  20.             }
  21.         }
  22.         return idx;
  23.     }
  24. }

6053. 统计网格图中没有被保卫的格子数

给你两个整数 m 和 n 表示一个下标从 0 开始的 m x n 网格图。同时给你两个二维整数数组 guards 和 walls ，其中 guards[i] = [rowi, coli] 且 walls[j] = [rowj, colj] ，分别表示第 i 个警卫和第 j 座墙所在的位置。
一个警卫能看到 4 个坐标轴方向（即东、南、西、北）的 所有 格子，除非他们被一座墙或者另外一个警卫 挡住 了视线。如果一个格子能被 至少 一个警卫看到，那么我们说这个格子被 保卫 了。
请你返回空格子中，有多少个格子是 没被保卫 的。

示例 1：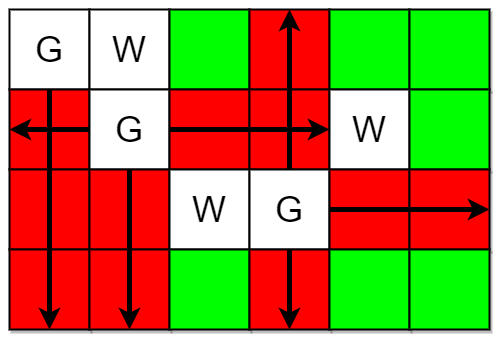
image.png
输入：m = 4, n = 6, guards = [[0,0],[1,1],[2,3]], walls = [[0,1],[2,2],[1,4]] 输出：7 解释：上图中，被保卫和没有被保卫的格子分别用红色和绿色表示。 总共有 7 个没有被保卫的格子，所以我们返回 7 。
示例 2：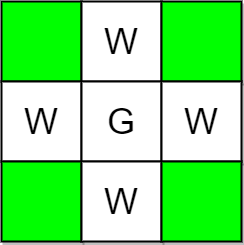
image.png
输入：m = 3, n = 3, guards = [[1,1]], walls = [[0,1],[1,0],[2,1],[1,2]] 输出：4 解释：上图中，没有被保卫的格子用绿色表示。 总共有 4 个没有被保卫的格子，所以我们返回 4 。

提示：

  • 1 <= m, n <= 105
  • 2 <= m * n <= 105
  • 1 <= guards.length, walls.length <= 5 * 104
  • 2 <= guards.length + walls.length <= m * n
  • guards[i].length == walls[j].length == 2
  • 0 <= rowi, rowj < m
  • 0 <= coli, colj < n
  • guards 和 walls 中所有位置 互不相同 。

思路：
四个方向分别考虑
时间复杂度: O(nm)
空间复杂度: O(nm)

  1. class Solution {
  2.     public int countUnguarded(int n, int m, int[][] guards, int[][] walls) {
  3.         int[][] st = new int[n][m];
  4.         for (int[] g : guards) {
  5.             st[g[0]][g[1]] = 2;
  6.         }
  7.         for (int[] w : walls) {
  8.             st[w[0]][w[1]] = -1;
  9.         }
  10.         for (int i = 0; i < n; i++) {
  11.             boolean flag = false;
  12.             for (int j = 0; j < m; j++) {
  13.                 if (st[i][j] == 2) {
  14.                     flag = true;
  15.                     continue;
  16.                 }
  17.                 if (st[i][j] == -1) {
  18.                     flag = false;
  19.                     continue;
  20.                 }
  21.                 if (flag)
  22.                     st[i][j] = 1;
  23.             }
  25.             flag = false;
  26.             for (int j = m - 1; j >= 0; j--) {
  27.                 if (st[i][j] == 2) {
  28.                     flag = true;
  29.                     continue;
  30.                 }
  31.                 if (st[i][j] == -1) {
  32.                     flag = false;
  33.                     continue;
  34.                 }
  35.                 if (flag)
  36.                     st[i][j] = 1;
  37.             }
  38.         }
  40.         for (int j = 0; j < m; j++) {
  41.             boolean flag = false;
  42.             for (int i = 0; i < n; i++) {
  43.                 if (st[i][j] == 2) {
  44.                     flag = true;
  45.                     continue;
  46.                 }
  47.                 if (st[i][j] == -1) {
  48.                     flag = false;
  49.                     continue;
  50.                 }
  51.                 if (flag)
  52.                     st[i][j] = 1;
  53.             }
  54.             flag = false;
  55.             for (int i = n - 1; i >= 0; i--) {
  56.                 if (st[i][j] == 2) {
  57.                     flag = true;
  58.                     continue;
  59.                 }
  60.                 if (st[i][j] == -1) {
  61.                     flag = false;
  62.                     continue;
  63.                 }
  64.                 if (flag)
  65.                     st[i][j] = 1;
  66.             }
  67.         }
  69.         int cnt = 0;
  70.         for (int i = 0; i < n; i++) {
  71.             for (int j = 0; j < m; j++) {
  72.                 if (st[i][j] == 0)
  73.                     cnt++;
  74.             }
  75.         }
  77.         // System.out.println(Arrays.deepToString(st));
  78.         return cnt;
  79.     }
  80. }

6054. 逃离火灾

给你一个下标从 0 开始大小为 m x n 的二维整数数组 grid ，它表示一个网格图。每个格子为下面 3 个值之一：

  • 0 表示草地。
  • 1 表示着火的格子。
  • 2 表示一座墙，你跟火都不能通过这个格子。

一开始你在最左上角的格子 (0, 0) ，你想要到达最右下角的安全屋格子 (m - 1, n - 1) 。每一分钟，你可以移动到 相邻 的草地格子。每次你移动 之后 ，着火的格子会扩散到所有不是墙的 相邻 格子。
请你返回你在初始位置可以停留的 最多 分钟数，且停留完这段时间后你还能安全到达安全屋。如果无法实现，请你返回 -1 。如果不管你在初始位置停留多久，你 总是 能到达安全屋，请你返回 109 。
注意，如果你到达安全屋后，火马上到了安全屋，这视为你能够安全到达安全屋。
如果两个格子有共同边，那么它们为 相邻 格子。

示例 1：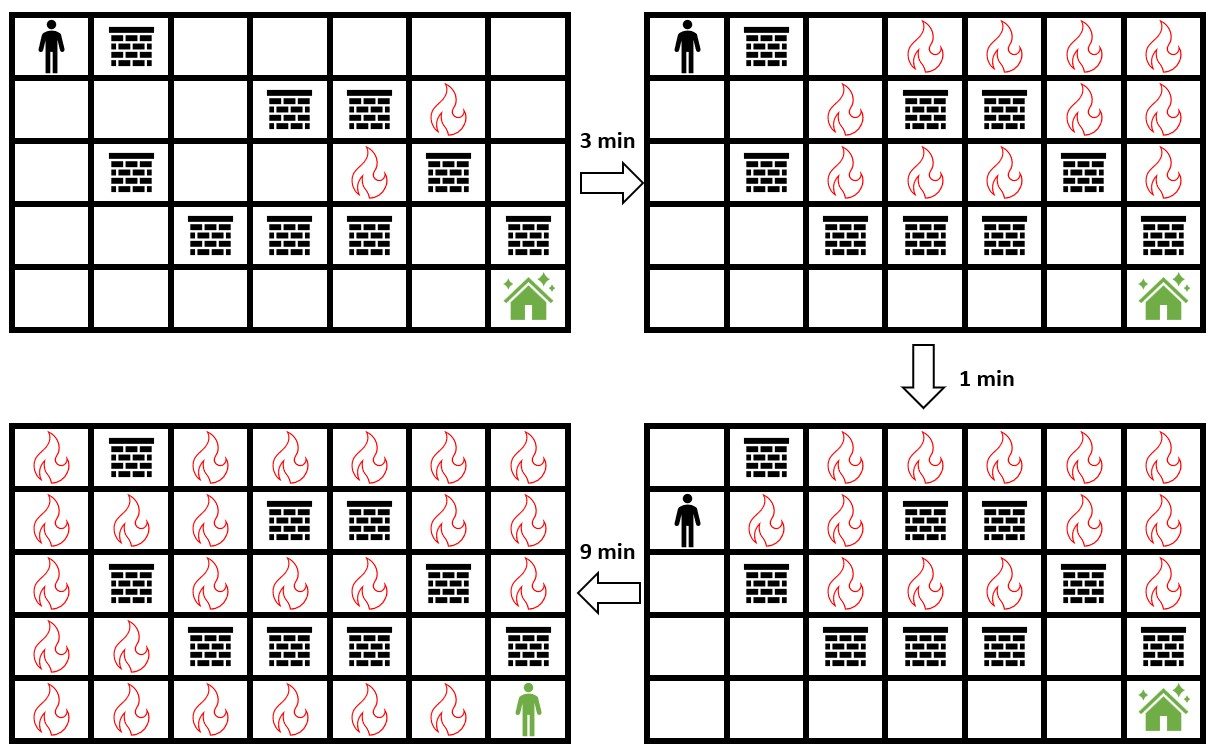
image.png
输入：grid = [[0,2,0,0,0,0,0],[0,0,0,2,2,1,0],[0,2,0,0,1,2,0],[0,0,2,2,2,0,2],[0,0,0,0,0,0,0]] 输出：3 解释：上图展示了你在初始位置停留 3 分钟后的情形。 你仍然可以安全到达安全屋。 停留超过 3 分钟会让你无法安全到达安全屋。
示例 2：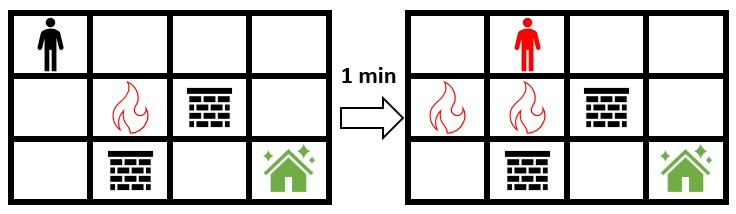
image.png
输入：grid = [[0,0,0,0],[0,1,2,0],[0,2,0,0]] 输出：-1 解释：上图展示了你马上开始朝安全屋移动的情形。 火会蔓延到你可以移动的所有格子，所以无法安全到达安全屋。 所以返回 -1 。
示例 3：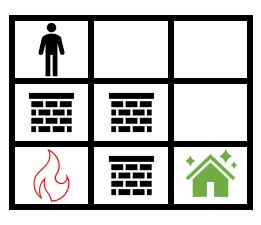
image.png
输入：grid = [[0,0,0],[2,2,0],[1,2,0]] 输出：1000000000 解释：上图展示了初始网格图。 注意，由于火被墙围了起来，所以无论如何你都能安全到达安全屋。 所以返回 109 。

提示：

  • m == grid.length
  • n == grid[i].length
  • 2 <= m, n <= 300
  • 4 <= m n <= 2 104
  • grid[i][j] 是 0 ，1 或者 2 。
  • grid[0][0] == grid[m - 1][n - 1] == 0

思路：
bfs + 二分
时间复杂度：O(nmlog(nm))
空间复杂度：O(nm)

  1. class Solution {
  2.     int n, m;
  3.     boolean[][] st;
  4.     int[][] p, f;
  5.     int inf = 1000000000;
  6.     public int maximumMinutes(int[][] grid) {
  7.         n = grid.length;
  8.         m = grid[0].length;
  9.         st = new boolean[n][m];
  10.         p = new int[n][m];
  11.         f = new int[n][m];
  12.         for (int i = 0; i < n; i++) {
  13.             Arrays.fill(f[i], -1);
  14.             Arrays.fill(p[i], -1);
  15.         }
  16.         bfs(grid);
  18.         if (!check(0, grid))
  19.             return -1;
  20.         if (check(inf, grid))
  21.             return inf;
  23.         int l = 0, r = inf;
  24.         while (l < r) {
  25.             int mid = l + r  + 1 >> 1;
  26.             if (check(mid, grid))
  27.                 l = mid;
  28.             else
  29.                 r = mid - 1;
  30.         }
  31.         return l;
  32.     }
  34.     boolean check(int w, int[][] grid) {
  35.         Queue<int[]> q = new LinkedList<>();
  36.         for (int i = 0; i < n; i++) {
  37.             Arrays.fill(st[i], false);
  38.         }
  39.         q.offer(new int[]{0, 0});
  40.         st[0][0] = true;
  42.         while (!q.isEmpty()) {
  43.             int[] cur = q.poll();
  44.             int x = cur[0], y = cur[1];
  45.             for (int i = 0; i < 4; i++) {
  46.                 int a = x + dx[i], b = y + dy[i];
  47.                 if (a < 0 || a >= n || b < 0 || b >= m || grid[a][b] == 2 || st[a][b])
  48.                     continue;
  49.                 if (a == n - 1 && b == m - 1 && (f[a][b] == -1 || p[a][b] + w <= f[a][b]))
  50.                     return true;
  51.                 if (f[a][b] == -1 || p[a][b] + w < f[a][b]) {
  52.                     st[a][b] = true;
  53.                     q.offer(new int[]{a, b});
  54.                 }
  55.             }
  56.         }
  58.         return false;
  59.     }
  61.     int[] dx = {-1, 0, 1, 0}, dy = {0, 1, 0, -1};
  63.     void bfs(int[][] grid) {
  64.         Queue<int[]> q = new LinkedList<>();
  66.         q.offer(new int[]{0, 0});
  67.         st[0][0] = true;
  68.         p[0][0] = 0;
  70.         int cnt = 0;
  71.         while (!q.isEmpty()) {
  72.             cnt++;
  73.             int size = q.size();
  74.             while (size -- > 0) {
  75.                 int[] cur = q.poll();
  76.                 int x = cur[0], y = cur[1];
  77.                 for (int i = 0; i < 4; i++) {
  78.                     int a = x + dx[i], b = y + dy[i];
  79.                     if (a < 0 || a >= n || b < 0 || b >= m || grid[a][b] == 2 || st[a][b])
  80.                         continue;
  81.                     st[a][b] = true;
  82.                     p[a][b] = cnt;
  83.                     q.offer(new int[]{a, b});
  84.                 }
  85.             }
  86.         }
  88.         for (int i = 0; i < n; i++) {
  89.             Arrays.fill(st[i], false);
  90.             for (int j = 0; j < m; j++) {
  91.                 if (grid[i][j] == 1) {
  92.                     q.offer(new int[]{i, j});
  93.                     st[i][j] = true;
  94.                     f[i][j] = 0;
  95.                 }
  96.             }
  97.         }
  98.         cnt = 0;
  99.         while (!q.isEmpty()) {
  100.             cnt++;
  101.             int size = q.size();
  102.             while (size -- > 0) {
  103.                 int[] cur = q.poll();
  104.                 int x = cur[0], y = cur[1];
  105.                 for (int i = 0; i < 4; i++) {
  106.                     int a = x + dx[i], b = y + dy[i];
  107.                     if (a < 0 || a >= n || b < 0 || b >= m || grid[a][b] == 2 || st[a][b])
  108.                         continue;
  109.                     st[a][b] = true;
  110.                     f[a][b] = cnt;
  111.                     q.offer(new int[]{a, b});
  112.                 }
  113.             }
  114.         }
  115.     }
  116. }