二维矩阵指每一行递增且每一列递增的整数二维矩阵

240. 搜索二维矩阵 II

编写一个高效的算法来搜索 _m_ x _n_ 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

  • 每行的元素从左到右升序排列。

  • 每列的元素从上到下升序排列。


    示例 1：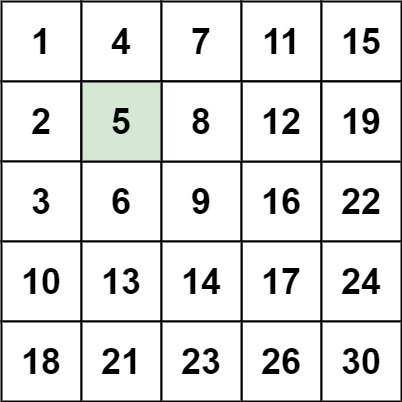
    二维矩阵问题 - 图1
    输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
    输出：true

示例 2：
二维矩阵问题 - 图2
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
输出：false


提示：

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= n, m <= 300
  • -10 <= matrix[i][j] <= 10
  • 每行的所有元素从左到右升序排列
  • 每列的所有元素从上到下升序排列
  • -10 <= target <= 10


  1. //从右上往左下搜索，每次排除一行或一列
  2. class Solution {
  3.     public boolean searchMatrix(int[][] matrix, int target) {
  4.         int n = matrix.length;
  5.         if (n == 0)
  6.             return false;
  7.         int m = matrix[0].length;
  8.         if (m == 0)
  9.             return false;
  10.         int i = 0, j = m - 1;
  11.         while (i < n && j >= 0) {
  12.             if (matrix[i][j] == target)
  13.                 return true;
  14.             else if (matrix[i][j] > target)
  15.                 j--;
  16.             else
  17.                 i++;
  18.         }
  19.         return false;
  20.     }
  21. }

378. 有序矩阵中第 K 小的元素

给你一个 n x n 矩阵 matrix ，其中每行和每列元素均按升序排序，找到矩阵中第 k 小的元素。
请注意，它是 排序后 的第 k 小元素，而不是第 k 个 不同 的元素。

示例 1：
输入：matrix = [[1,5,9],[10,11,13],[12,13,15]], k = 8
输出：13
解释：矩阵中的元素为 [1,5,9,10,11,12,13,13,15]，第 8 小元素是 13

示例 2：
输入：matrix = [[-5]], k = 1
输出：-5


提示：

  • n == matrix.length
  • n == matrix[i].length
  • 1 <= n <= 300
  • -10 <= matrix[i][j] <= 10
  • 题目数据 保证 matrix 中的所有行和列都按 非递减顺序 排列
  • 1 <= k <= n

思路：
相较于240，不是查询特定的数是否存在于二维矩阵中，而是问第k小的数是什么。
二分套二分可以解决！

  1. class Solution {
  2.     public int kthSmallest(int[][] g, int k) {
  3.         int n = g.length, m = g[0].length;
  4.         int min = g[0][0], max = g[n - 1][m - 1];
  6.         //二分结果
  7.         int l = min, r = max;
  8.         while (l < r) {
  9.             int mid = l + (r - l >> 1);
  10.             int c = 0;
  11.             //二分查找小于等于当前查找值(mid)的元素个数
  12.             for (int[] a : g) {
  13.                 int ll = 0, rr = m - 1;
  14.                 while (ll < rr) {
  15.                     int mm = ll + rr + 1 >> 1;
  16.                     if (a[mm] > mid)
  17.                         rr = mm - 1;
  18.                     else
  19.                         ll = mm;
  20.                 }
  21.                 if (a[ll] > mid)
  22.                     c += 0;
  23.                 else
  24.                     c += ll + 1;
  25.             }
  26.             if (c < k)
  27.                 l = mid + 1;
  28.             else
  29.                 r = mid;
  30.         }
  31.         return l;
  32.     }
  33. }

373. 查找和最小的K对数字

给定两个以升序排列的整数数组 nums1 和 nums2 , 以及一个整数 k 。
定义一对值 (u,v)，其中第一个元素来自 nums1，第二个元素来自 nums2 。
请找到和最小的 k 个数对 (u,v), (u,v) … (u,v) 。

示例 1:
输入: nums1 = [1,7,11], nums2 = [2,4,6], k = 3
输出: [1,2],[1,4],[1,6]
解释: 返回序列中的前 3 对数：
[1,2],[1,4],[1,6],[7,2],[7,4],[11,2],[7,6],[11,4],[11,6]

示例 2:
输入: nums1 = [1,1,2], nums2 = [1,2,3], k = 2
输出: [1,1],[1,1]
解释: 返回序列中的前 2 对数：
[1,1],[1,1],[1,2],[2,1],[1,2],[2,2],[1,3],[1,3],[2,3]

示例 3:
输入: nums1 = [1,2], nums2 = [3], k = 3
输出: [1,3],[2,3]
解释: 也可能序列中所有的数对都被返回:[1,3],[2,3]


提示:

  • 1 <= nums1.length, nums2.length <= 10
  • -10 <= nums1[i], nums2[i] <= 10
  • nums1, nums2 均为升序排列
  • 1 <= k <= 1000

思路：
相较于373：

  • 二维矩阵变成了两个数组的和构成的二维矩阵！
  • 最终结果不是查询第k小的数，而是返回前k小数对！

除了利用之前373的二分套二分以外，还可以使用多用归并！

  1. //二分套二分
  2. class Solution {
  3.     public List<List<Integer>> kSmallestPairs(int[] nums1, int[] nums2, int k) {
  4.         int n = nums1.length, m = nums2.length;
  5.         int min = nums1[0] + nums2[0], max = nums1[n - 1] + nums2[m - 1];
  7.         int l = min, r = max;
  8.         while (l < r) {
  9.             int mid = l + (r - l >> 1);
  10.             long c = 0;
  11.             for (int x : nums1) {
  12.                 if (x + nums2[m - 1] <= mid)
  13.                     c += m;
  14.                 else if (x + nums2[0] > mid) {
  15.                     break;
  16.                 } else {
  17.                     int ll = 0, rr = m - 1;
  18.                     while (ll < rr) {
  19.                         int mm = ll + (rr - ll + 1 >> 1);
  20.                         if (x + nums2[mm] > mid)
  21.                             rr = mm - 1;
  22.                         else
  23.                             ll = mm;
  24.                     }
  25.                     c += ll + 1;
  26.                 }
  27.             }
  28.             if (c < k)
  29.                 l = mid + 1;
  30.             else
  31.                 r = mid;
  32.         }
  33.         List<List<Integer>> res = new ArrayList<>(k);
  34.         Queue<List<Integer>> tmp = new LinkedList<>();
  35.         for (int x : nums1) {
  36.             for (int y : nums2) {
  37.                 if (x + y <= l) {
  38.                     List<Integer> arr = new ArrayList<>();
  39.                     arr.add(x);
  40.                     arr.add(y);
  41.                     if (x + y == l) {
  42.                         tmp.offer(arr);
  43.                         continue;
  44.                     }
  45.                     res.add(arr);
  46.                     k--;
  47.                 } else
  48.                     break;
  49.             }
  50.         }
  51.         while (k-- > 0 && !tmp.isEmpty()) {
  52.             res.add(tmp.poll());
  53.         }
  54.         return res;
  55.     }
  56. }
  1. //多路归并
  2. class Solution {
  3.     public List<List<Integer>> kSmallestPairs(int[] a, int[] b, int k) {
  4.         List<List<Integer>> res = new ArrayList<>(k);
  5.         int n = a.length, m = b.length;
  6.         PriorityQueue<int[]> q = new PriorityQueue<>((o1, o2) -> o1[0] - o2[0]);
  8.         for (int i = 0; i < m; i++)
  9.             q.offer(new int[]{a[0] + b[i], 0, i});
  11.         while (k-- > 0 && !q.isEmpty()) {
  12.             int[] cur = q.poll();
  13.             List<Integer> t = new ArrayList<>();
  14.             t.add(a[cur[1]]);
  15.             t.add(b[cur[2]]);
  16.             res.add(t);
  17.             if (cur[1] + 1 < n)
  18.                 q.offer(new int[]{a[cur[1] + 1] + b[cur[2]], cur[1] + 1, cur[2]});
  19.         }
  21.         return res;
  22.     }
  23. }

2040. 两个有序数组的第 K 小乘积

给你两个 从小到大排好序 且下标从 0 开始的整数数组 nums1 和 nums2 以及一个整数 k ，请你返回第 k （从 1 开始编号）小的 nums1[i] * nums2[j] 的乘积，其中 0 <= i < nums1.length 且 0 <= j < nums2.length 。

示例 1：

  1. 输入：nums1 = [2,5], nums2 = [3,4], k = 2
  2. 输出：8
  3. 解释：第 2 小的乘积计算如下：
  4. - nums1[0] * nums2[0] = 2 * 3 = 6
  5. - nums1[0] * nums2[1] = 2 * 4 = 8
  6. 第 2 小的乘积为 8 。

示例 2：

  1. 输入：nums1 = [-4,-2,0,3], nums2 = [2,4], k = 6
  2. 输出：0
  3. 解释：第 6 小的乘积计算如下：
  4. - nums1[0] * nums2[1] = (-4) * 4 = -16
  5. - nums1[0] * nums2[0] = (-4) * 2 = -8
  6. - nums1[1] * nums2[1] = (-2) * 4 = -8
  7. - nums1[1] * nums2[0] = (-2) * 2 = -4
  8. - nums1[2] * nums2[0] = 0 * 2 = 0
  9. - nums1[2] * nums2[1] = 0 * 4 = 0
  10. 第 6 小的乘积为 0 。

示例 3：

  1. 输入：nums1 = [-2,-1,0,1,2], nums2 = [-3,-1,2,4,5], k = 3
  2. 输出：-6
  3. 解释：第 3 小的乘积计算如下：
  4. - nums1[0] * nums2[4] = (-2) * 5 = -10
  5. - nums1[0] * nums2[3] = (-2) * 4 = -8
  6. - nums1[4] * nums2[0] = 2 * (-3) = -6
  7. 第 3 小的乘积为 -6 。

提示：

  • 1 <= nums1.length, nums2.length <= 5 * 10
  • -10 <= nums1[i], nums2[j] <= 10
  • 1 <= k <= nums1.length * nums2.length
  • nums1 和 nums2 都是从小到大排好序的。

思路：
相较于373，从两个数组各元素和变为两个数组各元素的乘积，特别是存在负数的情况！
由于本题是查找第k小的乘积是多少，而不是找前k小数对，不需要用多路归并(其实是因为会超时！！！)
所以用二分套二分即可！只是要注意正负的问题！
先判断第k小数位于正数还是负数范围内再处理！

  1. class Solution {
  2.     public long kthSmallestProduct(int[] nums1, int[] nums2, long k) {
  3.         List<Integer> a = new ArrayList<>();
  4.         List<Integer> b = new ArrayList<>();
  5.         List<Integer> na = new ArrayList<>();
  6.         List<Integer> nb = new ArrayList<>();
  7.         for (int x : nums1) {
  8.             if (x < 0)
  9.                 na.add(x);
  10.             else
  11.                 a.add(x);
  12.         }
  13.         for (int x : nums2) {
  14.             if (x < 0)
  15.                 nb.add(x);
  16.             else
  17.                 b.add(x);
  18.         }
  20.         long c = 1L * a.size() * nb.size() + b.size() * na.size();
  22.         long res = 0;
  23.         //正数情况
  24.         if (k > c) {
  25.             k -= c;
  26.             Collections.reverse(na);
  27.             Collections.reverse(nb);
  28.             res = get(k, a, b, na, nb);
  29.         } else {
  30.             Collections.reverse(a);
  31.             Collections.reverse(b);
  32.             res = get(k, a, nb, b, na);
  33.         }
  34.         return res;
  35.     }
  36.     long get(long k, List<Integer> a, List<Integer> b, List<Integer> na, List<Integer> nb) {
  37.         long res = 0;
  38.         long l = (long)(-1e10 - 10), r = (long)(1e10 + 10);
  39.         while (l < r) {
  40.             long mid = l + r >> 1;
  41.             long cnt = 0;
  43.             cnt += binarySearch(mid, a, b);
  44.             cnt += binarySearch(mid, na, nb);
  45.             if (cnt < k)
  46.                 l = mid + 1;
  47.             else
  48.                 r = mid;
  49.         }
  50.         return l;
  51.     }
  52.     long binarySearch(long mid, List<Integer> a, List<Integer> b) {
  53.         long cnt = 0;
  54.         if (a.size() == 0 || b.size() == 0)
  55.             return cnt;
  56.         for (Integer x : a) {
  57.             int ll = 0, rr = b.size() - 1;
  58.             while (ll < rr) {
  59.                 int mm = ll + (rr - ll + 1 >> 1);
  60.                 long val = 1L * x * b.get(mm);
  61.                 if (val > mid)
  62.                     rr = mm - 1;
  63.                 else
  64.                     ll = mm;
  65.             }
  66.             if (1L * x * b.get(ll) <= mid)
  67.                 cnt += ll + 1;
  68.         }
  69.         return cnt;
  70.     }
  71. }

668. 乘法表中第k小的数

几乎每一个人都用 乘法表。但是你能在乘法表中快速找到第k小的数字吗？
给定高度m 、宽度n 的一张 m * n的乘法表，以及正整数k，你需要返回表中第k 小的数字。
例 1：
输入: m = 3, n = 3, k = 5
输出: 3
解释:
乘法表:
1 2 3
2 4 6
3 6 9

第5小的数字是 3 (1, 2, 2, 3, 3).

例 2：
输入: m = 2, n = 3, k = 6
输出: 6
解释:
乘法表:
1 2 3
2 4 6

第6小的数字是 6 (1, 2, 2, 3, 4, 6).

注意：

  1. m 和 n 的范围在 [1, 30000] 之间。
  2. k 的范围在 [1, m * n] 之间。

思路：
类似于373，加法换成乘法

  1. class Solution {
  2.     public int findKthNumber(int m, int n, int k) {
  3.         int l = 1 * 1, r = m * n;
  5.         while (l < r) {
  6.             int mid = l + (r - l >> 1);
  7.             int cnt = get(m, n, mid);
  8.             if (cnt < k)
  9.                 l = mid + 1;
  10.             else
  11.                 r = mid;
  12.         }
  13.         return l;
  14.     }
  15.     int get(int m, int n, int x) {
  16.         int cnt = 0;
  18.         for (int i = 1; i <= n; i++) {
  19.             cnt += Math.min(x / i, m);
  20.         }
  21.         return cnt;
  22.     }
  23. }