性质：

  • 当前节点的左子树中的任何一个节点的权值 < 当前节点的权值
  • 当前节点的右子树中的任何一个节点的权值 > 当前节点的权值

如果有相同的值多次出现，用一个计数器统计即可。

作用：动态维护有序集合

插入

701. 二叉搜索树中的插入操作

给定二叉搜索树（BST）的根节点和要插入树中的值，将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ，新值和原始二叉搜索树中的任意节点值都不同。
注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。

示例 1：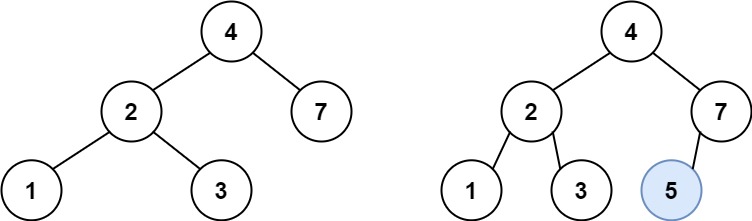
二叉搜索树 - 图1输入：root = [4,2,7,1,3], val = 5输出：[4,2,7,1,3,5]解释：另一个满足题目要求可以通过的树是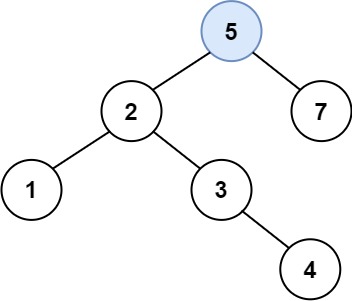：二叉搜索树 - 图2
示例 2：
输入：root = [40,20,60,10,30,50,70], val = 25
输出：[40,20,60,10,30,50,70,null,null,25]

示例 3：
输入：root = [4,2,7,1,3,null,null,null,null,null,null], val = 5
输出：[4,2,7,1,3,5]

提示：

  • 给定的树上的节点数介于 0 和 10^4 之间
  • 每个节点都有一个唯一整数值，取值范围从 0 到 10^8
  • -10^8 <= val <= 10^8
  • 新值和原始二叉搜索树中的任意节点值都不同

思路：

  1. 若树为空，将该值作为根节点插入
  2. 树不为空
    1. 若val < root.val，
      1. 左子树为空，插入到当前节点的左节点
      2. 递归在左子树中寻找插入位置
    2. 若val > root.val
      1. 右子树为空，插入到当前节点的右节点
      2. 递归在右子树中寻找插入位置

时间复杂度：O(h)，h为二叉搜索树的最大高度
空间复杂度：取决于递归法还是迭代法

  1. //递归
  2. class Solution {
  3.     public TreeNode insertIntoBST(TreeNode root, int val) {
  4.         if (root == null)
  5.             return new TreeNode(val);
  6.         dfs(root, val);
  7.         return root;
  8.     }
  9.     void dfs(TreeNode root, int val) {
  10.         if (root.val > val) {
  11.             if (root.left == null) {
  12.                 root.left = new TreeNode(val);
  13.                 return;
  14.             } else
  15.                 dfs(root.left, val);
  16.         } else {
  17.             if (root.right == null) {
  18.                 root.right = new TreeNode(val);
  19.                 return;
  20.             } else
  21.                 dfs(root.right, val);
  22.         }
  23.     }
  24. }
  25. //迭代
  26. class Solution {
  27.     public TreeNode insertIntoBST(TreeNode root, int val) {
  28.         if (root == null)
  29.             return new TreeNode(val);
  30.         TreeNode res = root;
  31.         while (true) {
  32.             if (root.val > val) {
  33.                 if (root.left == null) {
  34.                     root.left = new TreeNode(val);
  35.                     return res;
  36.                 } else {
  37.                     root = root.left;
  38.                 }
  39.             } else {
  40.                 if (root.right == null) {
  41.                     root.right = new TreeNode(val);
  42.                     return res;
  43.                 } else {
  44.                     root = root.right;
  45.                 }
  46.             }
  47.         }
  48.     }
  49. }

查找

700. 二叉搜索树中的搜索

给定二叉搜索树（BST）的根节点和一个值。 你需要在BST中找到节点值等于给定值的节点。 返回以该节点为根的子树。 如果节点不存在，则返回 NULL。
例如，
给定二叉搜索树:

  1.     4<br />       / \<br />      2   7<br />     / \<br />    1   3

和值: 2

你应该返回如下子树:
2
/ \
1 3

在上述示例中，如果要找的值是 5，但因为没有节点值为 5，我们应该返回 NULL。

思路：
利用二叉搜索树的性质

  1. 如果当前节点为空，说明没找到，返回null
  2. 如果当前节点val == val，返回当前节点
  3. 如果当前节点val > val，在左子树中寻找
  4. 如果当前节点val < val，在右子树中找

时间复杂度：O(h)，h为二叉搜索树的最大高度
空间复杂度：取决于递归法还是迭代法

  1. //递归
  2. class Solution {
  3.     public TreeNode searchBST(TreeNode root, int val) {
  4.         if (root == null)
  5.             return null;
  6.         if (root.val == val)
  7.             return root;
  8.         else if (root.val > val)
  9.             return searchBST(root.left,val);
  10.         else
  11.             return searchBST(root.right, val);
  12.     }
  13. }
  1. //迭代
  2. class Solution {
  3.     public TreeNode searchBST(TreeNode root, int val) {
  4.         while (root != null && root.val != val)
  5.             root = root.val > val ? root.left : root.right;
  6.         return root;
  7.     }
  8. }

删除

450. 删除二叉搜索树中的节点

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。
一般来说，删除节点可分为两个步骤：

  1. 首先找到需要删除的节点；

  2. 如果找到了，删除它。


    示例 1: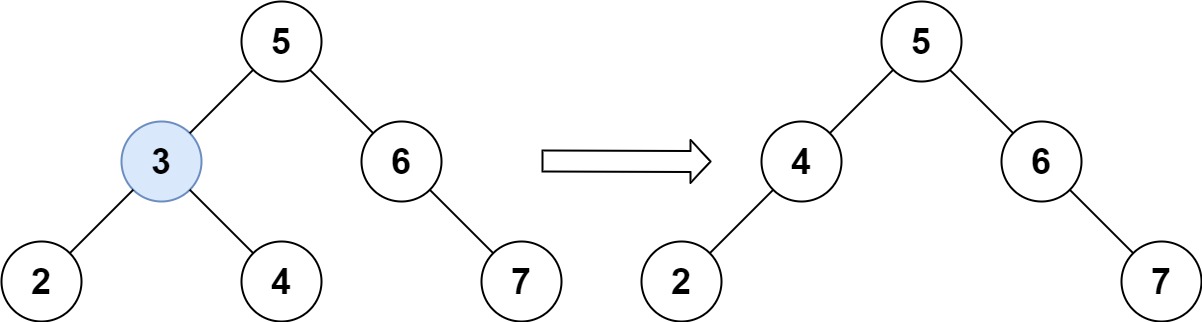
    二叉搜索树 - 图3
    输入：root = [5,3,6,2,4,null,7], key = 3输出：[5,4,6,2,null,null,7]解释：给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。 一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。 另一个正确答案是 [5,2,6,null,4,null,7]。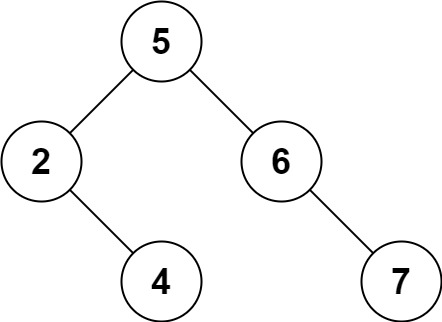 二叉搜索树 - 图4
    示例 2:
    输入: root = [5,3,6,2,4,null,7], key = 0
    输出: [5,3,6,2,4,null,7]
    解释: 二叉树不包含值为 0 的节点

示例 3:
输入: root = [], key = 0
输出: []

提示:

  • 节点数的范围 [0, 104].
  • -105 <= Node.val <= 105
  • 节点值唯一
  • root 是合法的二叉搜索树

  • -105 <= key <= 105


    进阶： 要求算法时间复杂度为 O(h)，h 为树的高度。

思路：
首先得知道二叉搜索树在中序遍历时的前驱和后继的概念
前驱指中序遍历排在当前点前一个位置的节点，后继指中序遍历排在当前点后一个位置的节点。
对于当前根节点来说，如果它的左子树不为空，则它的前驱节点为其左节点的最右侧节点，否则看其父节点，找到第一个左拐点，如果没有，说明当前节点不存在前驱，是全局最小值。
对于当前根节点来说，如果它的右子树不为空，则它的后继节点为其右子树的最左侧节点，否则看其父节点找到第一个右拐点，如果没有，说明当前节点不存在后继，是全局最大值。

对于本题来讲

  1. 若不存在待删除节点，返回根节点即可
  2. 若根节点值等于待删除值
    1. 若根节点既无前驱也无后继，返回null
    2. 若根节点有后继节点，用后继节点的值替换根节点，递归右子树删除后继节点，返回根节点
    3. 若根节点有前驱节点，用前驱节点的值替换根节点，递归左子树删除前驱节点。返回根节点
  3. 若根节点值大于待删除值，root.left = 递归在左子树中删除，返回根节点
  4. 若根节点值小于待删除值，root.right = 递归在右子树中删除，返回根节点

时间复杂度为 O(h)，h 为树的高度

  1. class Solution {
  2.     public TreeNode deleteNode(TreeNode root, int key) {
  3.         if (root == null)
  4.             return null;
  5.         if (root.val > key)
  6.             root.left = deleteNode(root.left, key);
  7.         else if (root.val < key) 
  8.             root.right = deleteNode(root.right, key);
  9.         else { //当前节点值等于val
  10.             if (root.left == null && root.right == null)
  11.                 root = null;
  12.             else if (root.right != null) {
  13.                 root.val = getSuccessor(root);
  14.                 root.right = deleteNode(root.right, root.val);
  15.             } else {
  16.                 root.val = getPredecessor(root);
  17.                 root.left = deleteNode(root.left, root.val);
  18.             }
  19.         }
  20.         return root;
  21.     }
  22.     int getPredecessor(TreeNode root) {
  23.         TreeNode cur = root.left;
  24.         while (cur.right != null)
  25.             cur = cur.right;
  26.         return cur.val;
  27.     }
  28.     int getSuccessor(TreeNode root) {
  29.         TreeNode cur = root.right;
  30.         while (cur.left != null)
  31.             cur = cur.left;
  32.         return cur.val;
  33.     }
  34. }

一个综合题

220. 存在重复元素 III

给你一个整数数组 nums 和两个整数 k 和 t 。请你判断是否存在 两个不同下标 i 和 j，使得 abs(nums[i] - nums[j]) <= t ，同时又满足 abs(i - j) <= k 。
如果存在则返回 true，不存在返回 false。

示例 1：
输入：nums = [1,2,3,1], k = 3, t = 0 输出：true
示例 2：
输入：nums = [1,0,1,1], k =_ _1, t = 2 输出：true
示例 3：
输入：nums = [1,5,9,1,5,9], k = 2, t = 3 输出：false

提示：

  • 0 <= nums.length <= 2 * 104
  • -2^31 <= nums[i] <= 2^31 - 1
  • 0 <= k <= 104
  • 0 <= t <= 2^31 - 1

思路：
如果本题使用二叉搜索树维护窗口，需要用到二叉搜索树的插入，删除以及查询操作（这里的查询是一种区间内的查询，区间中的任意一点都可以，也就是寻找最近公共祖先）。
更进一步：二叉搜索树由于本身不具有自动平衡的特性，所以使用红黑树效率更高，也就是Java的TreeSet数据结构
还有一种做法是使用桶排序，很巧妙的方法。

  1. //二叉树做法（又臭又长）
  2. class Solution {
  3.     class TreeNode {
  4.         int val;
  5.         TreeNode left, right;
  6.         TreeNode(int val) {
  7.             this.val = val;
  8.         }
  9.     }
  10.     public boolean containsNearbyAlmostDuplicate(int[] nums, int k, int t) {
  11.         TreeNode root = null;
  12.         for (int i = 0; i < nums.length; i++) {
  13.             if (i - k - 1 >= 0)
  14.                 root = delete(root, nums[i - k - 1]);
  15.             Integer large = 1L * t + nums[i] > Integer.MAX_VALUE ? Integer.MAX_VALUE : t + nums[i];
  16.             Integer small = nums[i] - 1L * t < Integer.MIN_VALUE ? Integer.MIN_VALUE : nums[i] - t;
  17.             TreeNode res = find(root, large, small);
  18.             if (res != null && res.val >= small && res.val <= large)
  19.                 return true;
  20.             root = add(root, nums[i]);
  21.         }
  22.         return false;
  23.     }
  25.     TreeNode delete(TreeNode root, int key) {
  26.         if (root == null)
  27.             return null;
  28.         if (key < root.val)
  29.             root.left = delete(root.left, key);
  30.         else if (key > root.val)
  31.             root.right = delete(root.right, key);
  32.         else {
  33.             TreeNode ne = getNext(root);
  34.             if (ne == null) return root.left;
  35.             else {
  36.                 root.val = ne.val;
  37.                 root.right = delete(root.right, root.val);
  38.             }
  39.         }
  40.         return root;
  41.     }
  42.     TreeNode getNext(TreeNode root) {
  43.         if (root == null || root.right == null)
  44.             return null;
  45.         root = root.right;
  46.         while (root.left != null)
  47.             root = root.left;
  48.         return root;
  49.     }
  51.     TreeNode add(TreeNode root, int val) {
  52.         if (root == null)
  53.             return new TreeNode(val);
  54.         if (val < root.val) {
  55.             if (root.left == null)
  56.                 root.left = new TreeNode(val);
  57.             else
  58.                 add(root.left, val);
  59.         } else if (val > root.val) {
  60.             if (root.right == null)
  61.                 root.right = new TreeNode(val);
  62.             else
  63.                 add(root.right, val);
  64.         }
  65.         return root;
  66.     }
  68.     TreeNode find(TreeNode root, int p, int q) {
  69.         if (root == null)
  70.             return null;
  71.         if (p > q)
  72.             return find(root, q, p);
  73.         if (p > root.val)
  74.             return find(root.right, p, q);
  75.         else if (q < root.val)
  76.             return find(root.left, p, q);
  77.         else
  78.             return root;
  79.     }
  80. }

其余方法见存在重复元素

扩展

带邻域的二叉搜索树能完成更多任务。

例如，每个节点的一个邻域为以当前节点为根节点的子树的总节点数。

703. 数据流中的第 K 大元素


设计一个找到数据流中第 k 大元素的类（class）。注意是排序后的第 k 大元素，不是第 k 个不同的元素。

请实现 KthLargest 类：

KthLargest(int k, int[] nums) 使用整数 k 和整数流 nums 初始化对象。
int add(int val) 将 val 插入数据流 nums 后，返回当前数据流中第 k 大的元素。

示例：

输入：
[“KthLargest”, “add”, “add”, “add”, “add”, “add”]
[[3, [4, 5, 8, 2]], [3], [5], [10], [9], [4]]
输出：
[null, 4, 5, 5, 8, 8]

解释：
KthLargest kthLargest = new KthLargest(3, [4, 5, 8, 2]);
kthLargest.add(3); // return 4
kthLargest.add(5); // return 5
kthLargest.add(10); // return 5
kthLargest.add(9); // return 8
kthLargest.add(4); // return 8

提示：
1 <= k <= 10^4
0 <= nums.length <= 10^4
-10^4 <= nums[i] <= 10^4
-10^4 <= val <= 10^4
最多调用 add 方法 10^4 次
题目数据保证，在查找第 k 大元素时，数组中至少有 k 个元素

思路：
方法1：使用带邻域的二叉树，更具有普适性！
方法2：使用优先队列

  1. //方法1：
  2. class KthLargest {
  3.     class TreeNode {
  4.         int val, cnt;
  5.         TreeNode left, right;
  6.         TreeNode (int val) {
  7.             this.val = val;
  8.         }
  9.         TreeNode(int val, int cnt) {
  10.             this.val = val;
  11.             this.cnt = cnt;
  12.         }
  13.     }
  14.     TreeNode root;
  15.     int k;
  16.     public KthLargest(int k, int[] nums) {
  17.         this.k = k;
  18.         for (int x : nums)
  19.             this.root = add(this.root, x);
  20.     }
  21.     private TreeNode add(TreeNode cur, int x) {
  22.         if (cur == null)
  23.             return new TreeNode(x, 1);
  24.         if (cur.val == x) {
  25.             int lcnt = cur.left == null ? 1 : cur.left.cnt + 1;
  26.             TreeNode newNode = new TreeNode(x, lcnt);
  27.             newNode.left = cur.left;
  28.             cur.left = newNode;
  29.             cur.cnt++;
  30.         } else if (x < cur.val) {
  31.             cur.left = add(cur.left, x);
  32.             cur.cnt = cur.right != null ? cur.right.cnt + cur.left.cnt + 1 : cur.left.cnt + 1;
  33.         } else if (x > cur.val) {
  34.             cur.right = add(cur.right, x);
  35.             cur.cnt = cur.left != null ? cur.left.cnt + cur.right.cnt + 1 : cur.right.cnt + 1;
  36.         }
  37.         return cur;
  38.     }
  40.     public int add(int val) {
  41.         this.root = add(this.root, val);
  42.         return find (this.root, this.k);
  43.     }
  44.     int find (TreeNode cur, int cnt) {
  45.         int cc = cur.right != null ? cur.right.cnt + 1 : 1;
  46.         if (cc == cnt)
  47.             return cur.val;
  48.         else if (cc > cnt)
  49.             return find(cur.right, cnt);
  50.         else
  51.             return find(cur.left, cnt - cc);
  52.     }
  54.     // private void print(TreeNode cur) {
  55.     //     if (cur == null)
  56.     //         return ;
  57.     //     print(cur.left);
  58.     //     System.out.print(cur.val + " " + cur.cnt + ", ");
  59.     //     print(cur.right);
  60.     // }
  61. }
  63. /**
  64.  * Your KthLargest object will be instantiated and called as such:
  65.  * KthLargest obj = new KthLargest(k, nums);
  66.  * int param_1 = obj.add(val);
  67.  */
  1. class KthLargest {
  2.     PriorityQueue<Integer> q = new PriorityQueue<>();
  3.     int k;
  4.     public KthLargest(int k, int[] nums) {
  5.         this.k = k;
  6.         for (int x : nums)
  7.             q.offer(x);
  8.     }
  10.     public int add(int val) {
  11.         q.offer(val);
  12.         while (q.size() > k)
  13.             q.poll();
  14.         return q.peek();
  15.     }
  16. }
  18. /**
  19.  * Your KthLargest object will be instantiated and called as such:
  20.  * KthLargest obj = new KthLargest(k, nums);
  21.  * int param_1 = obj.add(val);
  22.  */