🏆 第 289 场力扣周赛

保持良好的心态，虽然经历了昨晚的失利，但稳住就会有奇迹发生，今早又刷新了最好名次，是因为题简单吗(我觉得还好吧，而且没Wrong，这是最令人激动的)

6070. 计算字符串的数字和

给你一个由若干数字（0 - 9）组成的字符串 s ，和一个整数。
如果 s 的长度大于 k ，则可以执行一轮操作。在一轮操作中，需要完成以下工作：

1. 将 s 拆分 成长度为 k 的若干 连续数字组 ，使得前 k 个字符都分在第一组，接下来的 k 个字符都分在第二组，依此类推。注意，最后一个数字组的长度可以小于 k 。
2. 用表示每个数字组中所有数字之和的字符串来 替换 对应的数字组。例如，”346” 会替换为 “13” ，因为 3 + 4 + 6 = 13 。
3. 合并 所有组以形成一个新字符串。如果新字符串的长度大于 k 则重复第一步。

返回在完成所有轮操作后的 s 。

示例 1：
输入：s = “11111222223”, k = 3 输出：“135” 解释： - 第一轮，将 s 分成：”111”、”112”、”222” 和 “23” 。 接着，计算每一组的数字和：1 + 1 + 1 = 3、1 + 1 + 2 = 4、2 + 2 + 2 = 6 和 2 + 3 = 5 。 这样，s 在第一轮之后变成 “3” + “4” + “6” + “5” = “3465” 。 - 第二轮，将 s 分成：”346” 和 “5” 。 接着，计算每一组的数字和：3 + 4 + 6 = 13 、5 = 5 。 这样，s 在第二轮之后变成 “13” + “5” = “135” 。 现在，s.length <= k ，所以返回 “135” 作为答案。
示例 2：
输入：s = “00000000”, k = 3 输出：“000” 解释： 将 “000”, “000”, and “00”. 接着，计算每一组的数字和：0 + 0 + 0 = 0 、0 + 0 + 0 = 0 和 0 + 0 = 0 。 s 变为 “0” + “0” + “0” = “000” ，其长度等于 k ，所以返回 “000” 。

提示：

• 1 <= s.length <= 100
• 2 <= k <= 100
• s 仅由数字（0 - 9）组成。

思路：
递归处理即可

class Solution {
    public String digitSum(String s, int k) {
        if (s.length() <= k)
            return s;
        int n = s.length();
        StringBuilder sb = new StringBuilder();
        for (int i = 0; i < s.length(); i++) {
            int j = Math.min(n, i + k);
            String t = s.substring(i, j);
            sb.append(deal(t));
            i = j - 1;
        }
        return digitSum(sb.toString(), k);
    }
    int deal(String s) {
        int x = 0;
        for (int i = 0; i < s.length(); i++)
            x += s.charAt(i) - '0';
        return x;
    }
}

6071. 完成所有任务需要的最少轮数

给你一个下标从 0 开始的整数数组 tasks ，其中 tasks[i] 表示任务的难度级别。在每一轮中，你可以完成 2 个或者 3 个 相同难度级别 的任务。
返回完成所有任务需要的 最少 轮数，如果无法完成所有任务，返回 -1 。

示例 1：
输入：tasks = [2,2,3,3,2,4,4,4,4,4] 输出：4 解释：要想完成所有任务，一个可能的计划是： - 第一轮，完成难度级别为 2 的 3 个任务。 - 第二轮，完成难度级别为 3 的 2 个任务。 - 第三轮，完成难度级别为 4 的 3 个任务。 - 第四轮，完成难度级别为 4 的 2 个任务。 可以证明，无法在少于 4 轮的情况下完成所有任务，所以答案为 4 。
示例 2：
输入：tasks = [2,3,3] 输出：-1 解释：难度级别为 2 的任务只有 1 个，但每一轮执行中，只能选择完成 2 个或者 3 个相同难度级别的任务。因此，无法完成所有任务，答案为 -1 。

提示：

• 1 <= tasks.length <= 105
• 1 <= tasks[i] <= 109

思路：
贪心 + 分类讨论
能分3个一组就分3个一组，但有一点，只能分成每组2个或3个任务，而且所有任务都必须分出去
如果一个级别只有1个任务，无法分组
如果c % 3 == 0全部分成3个一组
如果c % 3 == 1最后4个任务两两一组，其它3个一组
如果c % 3 == 2最后2个任务两两一组，其它3个一组

class Solution {
    public int minimumRounds(int[] tasks) {
        int cnt = 0;
        Arrays.sort(tasks);
        int n = tasks.length;
        for (int i = 0; i < n; i++) {
            int j = i;
            while (j < n && tasks[j] == tasks[i])
                j++;
            int c = j - i;
            if (c == 1) return -1;
            if (c % 3 == 1) {
                cnt += 2;
                c -= 4;
                cnt += c / 3;
            } else if (c % 3 == 0) {
                cnt += c / 3;
            } else if (c % 3 == 2) {
                cnt += 1;
                c -= 2;
                cnt += c / 3;
            }
            i = j - 1;
        }
        return cnt;
    }
}

6072. 转角路径的乘积中最多能有几个尾随零

给你一个二维整数数组 grid ，大小为 m x n，其中每个单元格都含一个正整数。
转角路径 定义为：包含至多一个弯的一组相邻单元。具体而言，路径应该完全 向水平方向 或者 向竖直方向 移动过弯（如果存在弯），而不能访问之前访问过的单元格。在过弯之后，路径应当完全朝 另一个 方向行进：如果之前是向水平方向，那么就应该变为向竖直方向；反之亦然。当然，同样不能访问之前已经访问过的单元格。
一条路径的 乘积 定义为：路径上所有值的乘积。
请你从 grid 中找出一条乘积中尾随零数目最多的转角路径，并返回该路径中尾随零的数目。
注意：

• 水平 移动是指向左或右移动。
• 竖直 移动是指向上或下移动。

示例 1：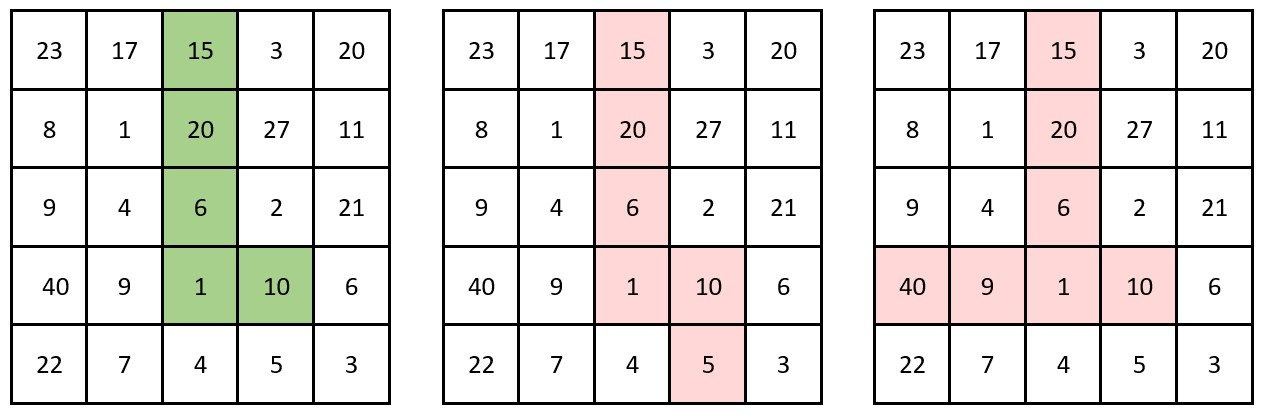

输入：grid = [[23,17,15,3,20],[8,1,20,27,11],[9,4,6,2,21],[40,9,1,10,6],[22,7,4,5,3]] 输出：3 解释：左侧的图展示了一条有效的转角路径。 其乘积为 15 20 6 1 10 = 18000 ，共计 3 个尾随零。 可以证明在这条转角路径的乘积中尾随零数目最多。 中间的图不是一条有效的转角路径，因为它有不止一个弯。 右侧的图也不是一条有效的转角路径，因为它需要重复访问已经访问过的单元格。
示例 2：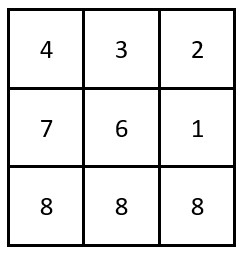

输入：grid = [[4,3,2],[7,6,1],[8,8,8]] 输出：0 解释：网格如上图所示。 不存在乘积含尾随零的转角路径。

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 105
• 1 <= m * n <= 105
• 1 <= grid[i][j] <= 1000

思路：
前缀和 + 数学
分解每个元素，统计2和5的因子数，后缀0只能由2 * 5得来
对于每个元素统计上下左右4个方向2和5的个数的前缀和
找最大的即可

时间复杂度：O(nm)
空间复杂度：O(nm)

class Solution {
    int n, m;
    int N = 100010;
    int[][] v2;
    int[][] v5;
    int[][][] up, down, left, right;
    public int maxTrailingZeros(int[][] g) {
        n = g.length;
        m = g[0].length;
        v2 = new int[n][m];
        v5 = new int[n][m];
        up = new int[n + 2][m + 2][2];
        down = new int[n + 2][m + 2][2];
        left = new int[n + 2][m + 2][2];
        right = new int[n + 2][m + 2][2];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                int x = g[i][j];
                int c2 = 0, c5 = 0;
                while (x % 2 == 0) {
                    c2++;
                    x /= 2;
                }
                while (x % 5 == 0) {
                    c5++;
                    x /= 5;
                }
                v2[i][j] = c2;
                v5[i][j] = c5;
            }
        }
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                left[i][j][0] += left[i][j - 1][0] + v2[i - 1][j - 1];
                left[i][j][1] += left[i][j - 1][1] + v5[i - 1][j - 1];
            }
            for (int j = m; j >= 1; j--) {
                right[i][j][0] += right[i][j + 1][0] + v2[i - 1][j - 1];
                right[i][j][1] += right[i][j + 1][1] + v5[i - 1][j - 1];
            }
        }
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                up[j][i][0] += up[j - 1][i][0] + v2[j - 1][i - 1];
                up[j][i][1] += up[j - 1][i][1] + v5[j - 1][i - 1];
            }
            for (int j = n; j >= 1; j--) {
                down[j][i][0] += down[j + 1][i][0] + v2[j - 1][i - 1];
                down[j][i][1] += down[j + 1][i][1] + v5[j - 1][i - 1];
            }
        }
        int max = 0;
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                max = Math.max(deal(up[i][j], left[i][j], v2[i - 1][j - 1], v5[i - 1][j - 1]), max);
                max = Math.max(deal(up[i][j], right[i][j], v2[i - 1][j - 1], v5[i - 1][j - 1]), max);
                max = Math.max(deal(down[i][j], left[i][j], v2[i - 1][j - 1], v5[i - 1][j - 1]), max);
                max = Math.max(deal(down[i][j], right[i][j], v2[i - 1][j - 1], v5[i - 1][j - 1]), max);
            }
        }
        return max;
    }
    int deal(int[] a, int[] b, int c2, int c5) {
        int x2 = a[0] + b[0] - c2;
        int x5 = a[1] + b[1] - c5;
        return Math.min(x2, x5);
    }
}

6073. 相邻字符不同的最长路径

给你一棵 树（即一个连通、无向、无环图），根节点是节点 0 ，这棵树由编号从 0 到 n - 1 的 n 个节点组成。用下标从 0 开始、长度为 n 的数组 parent 来表示这棵树，其中 parent[i] 是节点 i 的父节点，由于节点 0 是根节点，所以 parent[0] == -1 。
另给你一个字符串 s ，长度也是 n ，其中 s[i] 表示分配给节点 i 的字符。
请你找出路径上任意一对相邻节点都没有分配到相同字符的 最长路径 ，并返回该路径的长度。

示例 1：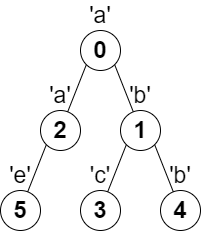

输入：parent = [-1,0,0,1,1,2], s = “abacbe” 输出：3 解释：任意一对相邻节点字符都不同的最长路径是：0 -> 1 -> 3 。该路径的长度是 3 ，所以返回 3 。 可以证明不存在满足上述条件且比 3 更长的路径。
示例 2：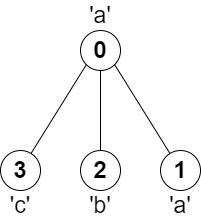

输入：parent = [-1,0,0,0], s = “aabc” 输出：3 解释：任意一对相邻节点字符都不同的最长路径是：2 -> 0 -> 3 。该路径的长度为 3 ，所以返回 3 。

提示：

• n == parent.length == s.length
• 1 <= n <= 105
• 对所有 i >= 1 ，0 <= parent[i] <= n - 1 均成立
• parent[0] == -1
• parent 表示一棵有效的树
• s 仅由小写英文字母组成

思路：
经典树形DP找最长路径

class Solution {
    int N = 100010;
    int[] h = new int[N], e = new int[N], ne = new int[N];
    int idx = 0;
    int n;
    char[] ch;
    int max = 0;
    // int[] w = new int[N];
    public int longestPath(int[] parent, String s) {
        this.n = parent.length;
        ch = s.toCharArray();
        Arrays.fill(h, -1);
        for (int i = 1; i < n; i++) {
            int a = parent[i], b = i;
            add(a, b);
        }
        dfs(0);
        return max + 1;
    }
    int dfs(int u) {
        int d1 = 0, d2 = 0;
        for (int i = h[u]; i != -1; i = ne[i]) {
            int j = e[i];
            int d = dfs(j) + 1;
            if (ch[j] == ch[u]) continue;
            if (d >= d1) {
                d2 = d1;
                d1 = d;
            } else if (d >= d2) {
                d2 = d;
            }
        }
        max = Math.max(max, d1 + d2);
        return d1;
    }
    void add(int a, int b) {
        e[idx] = b;
        ne[idx] = h[a];
        h[a] = idx++;
    }
}