周赛 - 😺 第 68 场力扣夜喵双周赛 - 《学习笔记》

哭了，心态优点微妙的变化，第三题疯狂wrong，但也没那么难。
括号问题还是得加练！
第四题是真的没想到，赛后有大佬提出标准答案都给错了。。。
还是参考下第一名的解法！uwi牛逼

5946. 句子中的最多单词数

一个句子由一些单词以及它们之间的单个空格组成，句子的开头和结尾不会有多余空格。
给你一个字符串数组 sentences ，其中 sentences[i] 表示单个句子。
请你返回单个句子里 单词的最多数目 。

示例 1：
输入：sentences = [“alice and bob love leetcode”, “i think so too”, “this is great thanks very much”] 输出：6 解释： - 第一个句子 “alice and bob love leetcode” 总共有 5 个单词。 - 第二个句子 “i think so too” 总共有 4 个单词。 - 第三个句子 “this is great thanks very much” 总共有 6 个单词。所以，单个句子中有最多单词数的是第三个句子，总共有 6 个单词。
示例 2：
输入：sentences = [“please wait”, “continue to fight”, “continue to win”] 输出：3 解释：可能有多个句子有相同单词数。这个例子中，第二个句子和第三个句子（加粗斜体）有相同数目的单词数。

提示：

1 <= sentences.length <= 100
1 <= sentences[i].length <= 100
sentences[i] 只包含小写英文字母和 ‘ ‘ 。
sentences[i] 的开头和结尾都没有空格。
sentences[i] 中所有单词由单个空格隔开。

思路：
返回句子的最大单词数，直接调库

class Solution {
    public int mostWordsFound(String[] sentences) {
        int max = 0;
        for (String s : sentences) {
            max = Math.max(max, s.split(" ").length);
        }
        return max;
    }
}

5947. 从给定原材料中找到所有可以做出的菜

你有 n 道不同菜的信息。给你一个字符串数组 recipes 和一个二维字符串数组 ingredients 。第 i 道菜的名字为 recipes[i] ，如果你有它所有的原材料 ingredients[i] ，那么你可以做出这道菜。一道菜的原材料可能是 另一道 菜，也就是说 ingredients[i] 可能包含 recipes 中另一个字符串。
同时给你一个字符串数组 supplies ，它包含你初始时拥有的所有原材料，每一种原材料你都有无限多。
请你返回你可以做出的所有菜。你可以以 任意顺序 返回它们。
注意两道菜在它们的原材料中可能互相包含。

示例 1：
输入：recipes = [“bread”], ingredients = [[“yeast”,”flour”]], supplies = [“yeast”,”flour”,”corn”] 输出：[“bread”] 解释： 我们可以做出 “bread” ，因为我们有原材料 “yeast” 和 “flour” 。
示例 2：
输入：recipes = [“bread”,”sandwich”], ingredients = [[“yeast”,”flour”],[“bread”,”meat”]], supplies = [“yeast”,”flour”,”meat”] 输出：[“bread”,”sandwich”] 解释： 我们可以做出 “bread” ，因为我们有原材料 “yeast” 和 “flour” 。我们可以做出 “sandwich” ，因为我们有原材料 “meat” 且可以做出原材料 “bread” 。
示例 3：
输入：recipes = [“bread”,”sandwich”,”burger”], ingredients = [[“yeast”,”flour”],[“bread”,”meat”],[“sandwich”,”meat”,”bread”]], supplies = [“yeast”,”flour”,”meat”] 输出：[“bread”,”sandwich”,”burger”] 解释： 我们可以做出 “bread” ，因为我们有原材料 “yeast” 和 “flour” 。我们可以做出 “sandwich” ，因为我们有原材料 “meat” 且可以做出原材料 “bread” 。我们可以做出 “burger” ，因为我们有原材料 “meat” 且可以做出原材料 “bread” 和 “sandwich” 。
示例 4：
输入：recipes = [“bread”], ingredients = [[“yeast”,”flour”]], supplies = [“yeast”] 输出：[] 解释： 我们没法做出任何菜，因为我们只有原材料 “yeast” 。

提示：

n == recipes.length == ingredients.length
1 <= n <= 100
1 <= ingredients[i].length, supplies.length <= 100
1 <= recipes[i].length, ingredients[i][j].length, supplies[k].length <= 10
recipes[i], ingredients[i][j] 和 supplies[k] 只包含小写英文字母。
所有 recipes 和 supplies 中的值互不相同。
ingredients[i] 中的字符串互不相同。

思路：
数据范围很小，所以可以暴力循环n次，确保没有新菜能被做出
时间复杂度：o(n^3)

更好的做法是拓扑排序 + bfs

class Solution {
    public List<String> findAllRecipes(String[] recipes, List<List<String>> ingredients, String[] supplies) {
        Set<String> set = new HashSet<>();
        for (String s : supplies)
            set.add(s);
        int n = recipes.length;
        boolean[] st = new boolean[n];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                if (st[j]) continue;
                boolean flag = true;
                for (String s : ingredients.get(j)) {
                    if (!set.contains(s)) {
                        flag = false;
                        break;
                    }
                }
                if (flag) {
                    st[j] = true;
                    set.add(recipes[j]);
                }
            }
        }
        List<String> res = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            if (st[i])
                res.add(recipes[i]);
        }
        return res;
    }
}

// 拓扑
class Solution {
    public List<String> findAllRecipes(String[] recipes, List<List<String>> ingredients, String[] supplies) {
        Map<String, List<String>> edge = new HashMap<>();
        Map<String, Integer> in = new HashMap<>();
        int n = recipes.length;
        for (int i = 0; i < n; i++) {
            String y = recipes[i];
            for (String x : ingredients.get(i)) {
                edge.putIfAbsent(x, new ArrayList<>());
                edge.get(x).add(y);
                in.merge(y, 1, Integer::sum);
            }
        }
        Queue<String> q = new LinkedList<>();
        for (String s : supplies) {
            q.offer(s);
        }
        List<String> res = new ArrayList<>();
        while(!q.isEmpty()) {
            String cur = q.poll();
            for (String s : edge.getOrDefault(cur, new ArrayList<>())) {
                in.merge(s, -1, Integer::sum);
                if (in.get(s) == 0) {
                    res.add(s);
                    q.offer(s);
                }
            }
        }
        return res;
    }
}

5948. 判断一个括号字符串是否有效

一个括号字符串是只由 ‘(‘ 和 ‘)’ 组成的非空字符串。如果一个字符串满足下面任意一个条件，那么它就是有效的：

字符串为 ().
它可以表示为 AB（A 与 B 连接），其中A 和 B 都是有效括号字符串。
它可以表示为 (A) ，其中 A 是一个有效括号字符串。

给你一个括号字符串 s 和一个字符串 locked ，两者长度都为 n 。locked 是一个二进制字符串，只包含 ‘0’ 和 ‘1’ 。对于 locked 中 每一个 下标 i ：

如果 locked[i] 是 ‘1’ ，你不能改变 s[i] 。
如果 locked[i] 是 ‘0’ ，你可以将 s[i] 变为 ‘(‘ 或者 ‘)’ 。

如果你可以将 s 变为有效括号字符串，请你返回 true ，否则返回 false 。

示例 1：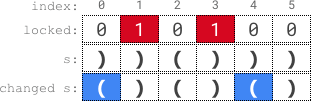

输入：s = “))()))”, locked = “010100” 输出：true 解释：locked[1] == ‘1’ 和 locked[3] == ‘1’ ，所以我们无法改变 s[1] 或者 s[3] 。我们可以将 s[0] 和 s[4] 变为 ‘(‘ ，不改变 s[2] 和 s[5] ，使 s 变为有效字符串。
示例 2：
输入：s = “()()”, locked = “0000” 输出：true 解释：我们不需要做任何改变，因为 s 已经是有效字符串了。
示例 3：
输入：s = “)”, locked = “0” 输出：false 解释：locked 允许改变 s[0] 。但无论将 s[0] 变为 ‘(‘ 或者 ‘)’ 都无法使 s 变为有效字符串。

提示：

n == s.length == locked.length
1 <= n <= 105
s[i] 要么是 ‘(‘ 要么是 ‘)’ 。
locked[i] 要么是 ‘0’ 要么是 ‘1’ 。

思路：
类似于678题，可变化的括号可以认为是通配符。
首先得保证总个数为偶数
从左往右，从右往左各一遍，就能却能是否合法。
从左往右时把通配符当成左括号，能匹配左括号优先匹配左括号，不能匹配左括号时匹配通配符。若都没有，返回false
再从右往左一遍是因为上一轮遍历只能确定右括号能被正确匹配，需要保证左括号也能被正确匹配。

class Solution {
    public boolean canBeValid(String s, String locked) {
        int n = s.length();
        if (n % 2 != 0) return false;
        int u = 0, left = 0, right = 0;
        for (int i = 0; i < n; i++) {
            if (locked.charAt(i) == '0')
                u++;
            else {
                if (s.charAt(i) == '(')
                    left++;
                else {
                    if (left > 0)
                        left--;
                    else if (u > 0)
                        u--;
                    else
                        return false;
                }
            }
        }
        u = 0;
        for (int i = n - 1; i >= 0; i--) {
            if (locked.charAt(i) == '0')
                u++;
            else {
                if (s.charAt(i) == ')')
                    right++;
                else {
                    if (right > 0)
                        right--;
                    else if (u > 0)
                        u--;
                    else
                        return false;
                }
            }
        }
        return true;
    }
}

//当然，用栈也能做
class Solution {
    public boolean canBeValid(String s, String locked) {
        Deque<Integer> star = new LinkedList<>();
        Deque<Integer> left = new LinkedList<>();
        int n = s.length();
        if (n % 2 != 0) return false;
        for (int i = 0; i < n; i++) {
            if (locked.charAt(i) == '0')
                star.push(i);
            else {
                if (s.charAt(i) == '(')
                    left.push(i);
                else {
                    if (!left.isEmpty())
                        left.pop();
                    else if (!star.isEmpty())
                        star.pop();
                    else
                        return false;
                }
            }
        }
        while (!left.isEmpty()) {
            int a = left.pop();
            if (star.isEmpty())
                return false;
            int b = star.pop();
            if (b < a)
                return false;
        }
        return true;
    }
}

5949. 一个区间内所有数乘积的缩写

给你两个正整数 left 和 right ，满足 left <= right 。请你计算 闭区间 [left, right] 中所有整数的乘积。
由于乘积可能非常大，你需要将它按照以下步骤缩写：

统计乘积中后缀 0 的数目，将这个数目记为 C 。
比方说，1000 中有 3 个后缀 0 ，546 中没有后缀 0 。

将乘积中剩余数字记为 d 。如果 d > 10 ，那么将乘积表示为

… 的形式，其中  表示乘积最 开始 的 5 个数位， 表示删除后缀 0 之后 结尾的 5 个数位。如果 d <= 10 ，我们不对它做修改。
比方说，我们将 1234567654321 表示为 12345…54321 ，但是 1234567 仍然表示为 1234567 。

最后，将乘积表示为 字符串 “

…eC” 。
比方说，12345678987600000 被表示为 “12345…89876e5” 。

请你返回一个字符串，表示 闭区间 [left, right] 中所有整数乘积的缩写。

示例 1：
输入：left = 1, right = 4 输出：“24e0” 解释： 乘积为 1 × 2 × 3 × 4 = 24 。由于没有后缀 0 ，所以 24 保持不变，缩写的结尾为 “e0” 。因为乘积的结果是 2 位数，小于 10 ，所欲我们不进一步将它缩写。所以，最终将乘积表示为 “24e0” 。
示例 2：
输入：left = 2, right = 11 输出：“399168e2” 解释： 乘积为 39916800 。有 2 个后缀 0 ，删除后得到 399168 。缩写的结尾为 “e2” 。删除后缀 0 后是 6 位数，不需要进一步缩写。所以，最终将乘积表示为 “399168e2” 。
示例 3：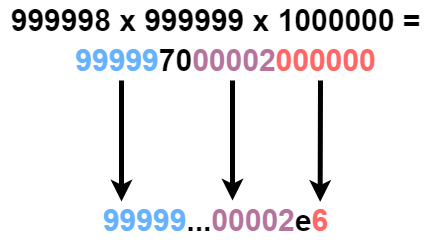

输入：left = 999998, right = 1000000 输出：“99999…00002e6” 解释： 上图展示了如何得到乘积的缩写 “99999…00002e6” 。 - 总共有 6 个后缀 0 。缩写的结尾为 “e6” 。 - 开头 5 个数位是 99999 。 - 删除后缀 0 后结尾 5 个数字为 00002 。
示例 4：
输入：left = 256, right = 65535 输出：“23510…78528e16317” 解释： 乘积是一个非常大的数字： - 总共有 16317 个后缀 0 。缩写结尾为 “e16317” 。 - 开头 5 个数字为 23510 。 - 删除后缀 0 后，结尾 5 个数字为 78528 。所以，乘积的缩写为 “23510…78528e16317” 。

提示：

1 <= left <= right <= 106

思路：
求的过程中判断结果是不是会大于等于10位
分三部分求：
末尾0有多少个，0肯定是用2 * 5 得来的，所以对2和5进行分集即可
低5位，这个简单，边算边取模即可
高5位，这个太难了，首先排除用long直接算，精度损失过大。故考虑使用double，虽然能过，但是题解区有人能卡掉，更准确的精度确实不知道如何计算了，可能需要128位的double了。。。

class Solution {
    public String abbreviateProduct(int left, int right) {
        double pre = 1.0, tf = 1.0;
        long rem = 1L;
        long c = 0, e = 0, c2 = 0, c5 = 0;
        for (int i = left; i <= right; i++) {
            pre *= i;
            while (pre > 10000000000.0) {
                pre /= 10;
            }
            tf *= i;
            while (tf >= 10) {
                e++;
                tf /= 10;
            }
            int j = i;
            while (j % 2 == 0) {
                c2 ++;
                j /= 2;
            }
            while (j % 5 == 0) {
                c5 ++;
                j /= 5;
            }
            rem *= j;
            rem %= 100000;
        }
        long d = Math.min(c2, c5);
        c2 -= d;
        c5 -= d;
        int x = c2 == 0 ? 5 : 2;
        c2 = c2 == 0 ? c5 : c2;
        while (c2 > 0) {
            c2--;
            rem *= x;
            rem %= 100000;
        }
        if (e - d <= 9) {
            long v = (long)(pre);
            while (v % 10 == 0)
                v /= 10;
            return v + "e" + d;
        } else {
            // System.out.println(pre);
            return String.valueOf((long)(pre)).substring(0, 5) + "..." + String.format("%05d", rem) + "e" + d;
        }
    }
}