周赛 - 🏆 第 312 场力扣周赛 - 《学习笔记》

6188. 按身高排序
6189. 按位与最大的最长子数组
6190. 找到所有好下标
6191. 好路径的数目

去北校区忙搬实验室了，没有参加，有点遗憾

6188. 按身高排序

给你一个字符串数组 names ，和一个由 互不相同 的正整数组成的数组 heights 。两个数组的长度均为 n 。
对于每个下标 i，names[i] 和 heights[i] 表示第 i 个人的名字和身高。
请按身高降序顺序返回对应的名字数组 names 。

示例 1：
输入：names = [“Mary”,”John”,”Emma”], heights = [180,165,170] 输出：[“Mary”,”Emma”,”John”] 解释：Mary 最高，接着是 Emma 和 John 。
示例 2：
输入：names = [“Alice”,”Bob”,”Bob”], heights = [155,185,150] 输出：[“Bob”,”Alice”,”Bob”] 解释：第一个 Bob 最高，然后是 Alice 和第二个 Bob 。

提示：

n == names.length == heights.length
1 <= n <= 103
1 <= names[i].length <= 20
1 <= heights[i] <= 105
names[i] 由大小写英文字母组成
heights 中的所有值互不相同

思路：
排个序即可

class Solution {
    public String[] sortPeople(String[] names, int[] heights) {
        int n = names.length;
        Pair[] p = new Pair[n];
        for (int i = 0; i < n; i++) {
            p[i] = new Pair(names[i], heights[i]);
        }
        Arrays.sort(p, (o1, o2) -> (o2.height - o1.height));
        for (int i = 0; i < n; i++)
            names[i] = p[i].name;
        return names;
    }
    class Pair {
        String name;
        int height;
        Pair(String name, int height) {
            this.name = name;
            this.height = height;
        }
    }
}

6189. 按位与最大的最长子数组

给你一个长度为 n 的整数数组 nums 。
考虑 nums 中进行 按位与（bitwise AND）运算得到的值最大的非空子数组。

换句话说，令 k 是 nums 任意子数组执行按位与运算所能得到的最大值。那么，只需要考虑那些执行一次按位与运算后等于 k 的子数组。

返回满足要求的最长子数组的长度。
数组的按位与就是对数组中的所有数字进行按位与运算。
子数组 是数组中的一个连续元素序列。

示例 1：
输入：nums = [1,2,3,3,2,2] 输出：2 解释： 子数组按位与运算的最大值是 3 。能得到此结果的最长子数组是 [3,3]，所以返回 2 。
示例 2：
输入：nums = [1,2,3,4] 输出：1 解释： 子数组按位与运算的最大值是 4 。能得到此结果的最长子数组是 [4]，所以返回 1 。

提示：

1 <= nums.length <= 105
1 <= nums[i] <= 106

思路：
即找数组最大值的连续出现次数的最大值

class Solution {
    public int longestSubarray(int[] nums) {
        int max = 0;
        for (int x : nums) max = Math.max(max, x);
        int len = 0;
        for (int i = 0; i < nums.length; i++) {
            if (nums[i] == max) {
                int j = i;
                while (j < nums.length && nums[j] == max)
                    j++;
                len = Math.max(j - i, len);
                i = j - 1;
            }
        }
        return len;
    }
}

6190. 找到所有好下标

给你一个大小为 n 下标从 0 开始的整数数组 nums 和一个正整数 k 。
对于 k <= i < n - k 之间的一个下标 i ，如果它满足以下条件，我们就称它为一个好下标：

下标 i 之前的 k 个元素是 非递增的 。
下标 i 之后的 k 个元素是 非递减的 。

按升序返回所有好下标。

示例 1：
输入：nums = [2,1,1,1,3,4,1], k = 2 输出：[2,3] 解释：数组中有两个好下标： - 下标 2 。子数组 [2,1] 是非递增的，子数组 [1,3] 是非递减的。 - 下标 3 。子数组 [1,1] 是非递增的，子数组 [3,4] 是非递减的。注意，下标 4 不是好下标，因为 [4,1] 不是非递减的。
示例 2：
输入：nums = [2,1,1,2], k = 2 输出：[] 解释：数组中没有好下标。

提示：

n == nums.length
3 <= n <= 105
1 <= nums[i] <= 106
1 <= k <= n / 2

思路：
线性DP

class Solution {
    public List<Integer> goodIndices(int[] nums, int k) {
        int n = nums.length;
        int[] left = new int[n], right = new int[n];
        left[0] = 1;
        for (int i = 1; i < n; i++) {
            if (nums[i] <= nums[i - 1])
                left[i] = left[i - 1] + 1;
            else left[i] = 1;
        }
        right[n - 1] = 1;
        for (int i = n - 2; i >= 0; i--) {
            if (nums[i] <= nums[i + 1])
                right[i] = right[i + 1] + 1;
            else right[i] = 1;
        }
        List<Integer> res = new ArrayList<>();
        for (int i = 1; i < n - 1; i++) {
            if (left[i - 1] >= k && right[i + 1] >= k)
                res.add(i);
        }
        return res;
    }
}

6191. 好路径的数目

显示英文描述
我的提交返回竞赛

通过的用户数280
尝试过的用户数1024
用户总通过次数345
用户总提交次数2602
题目难度Hard

给你一棵 n 个节点的树（连通无向无环的图），节点编号从 0 到 n - 1 且恰好有 n - 1 条边。
给你一个长度为 n 下标从 0 开始的整数数组 vals ，分别表示每个节点的值。同时给你一个二维整数数组 edges ，其中 edges[i] = [ai, bi] 表示节点 ai 和 bi 之间有一条无向边。
一条 好路径 需要满足以下条件：

开始节点和结束节点的值相同。
开始节点和结束节点中间的所有节点值都 小于等于 开始节点的值（也就是说开始节点的值应该是路径上所有节点的最大值）。

请你返回不同好路径的数目。
注意，一条路径和它反向的路径算作同一路径。比方说， 0 -> 1 与 1 -> 0 视为同一条路径。单个节点也视为一条合法路径。

示例 1：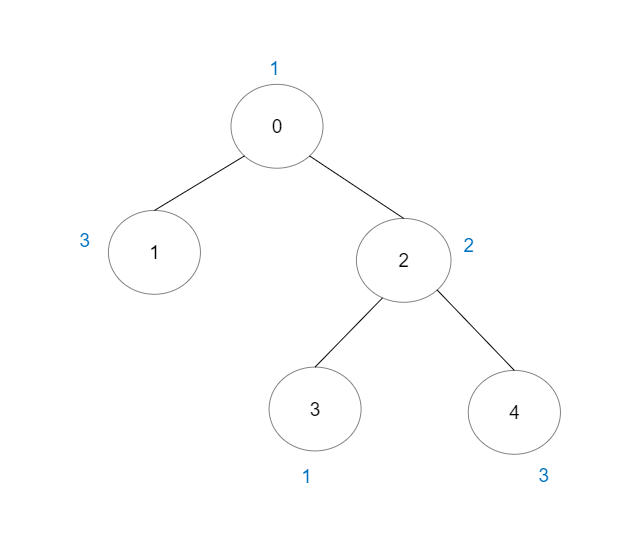

输入：vals = [1,3,2,1,3], edges = [[0,1],[0,2],[2,3],[2,4]] 输出：6 解释：总共有 5 条单个节点的好路径。还有 1 条好路径：1 -> 0 -> 2 -> 4 。（反方向的路径 4 -> 2 -> 0 -> 1 视为跟 1 -> 0 -> 2 -> 4 一样的路径）注意 0 -> 2 -> 3 不是一条好路径，因为 vals[2] > vals[0] 。
示例 2：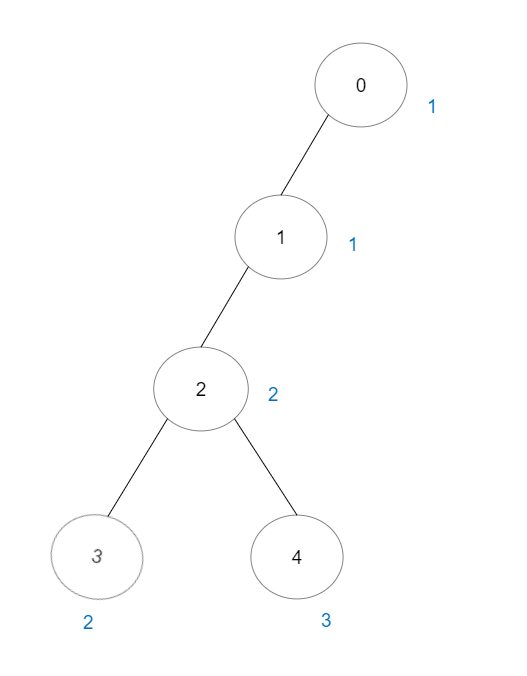

输入：vals = [1,1,2,2,3], edges = [[0,1],[1,2],[2,3],[2,4]] 输出：7 解释：总共有 5 条单个节点的好路径。还有 2 条好路径：0 -> 1 和 2 -> 3 。
示例 3：

输入：vals = [1], edges = [] 输出：1 解释：这棵树只有一个节点，所以只有一条好路径。

提示：

n == vals.length
1 <= n <= 3 * 104
0 <= vals[i] <= 105
edges.length == n - 1
edges[i].length == 2
0 <= ai, bi < n
ai != bi
edges 表示一棵合法的树。

思路：
排序 + 并查集

class Solution {
    public int numberOfGoodPaths(int[] vals, int[][] edges) {
        Arrays.sort(edges, (o1, o2) -> {
            int a = Math.max(vals[o1[0]], vals[o1[1]]), b = Math.max(vals[o2[0]], vals[o2[1]]);
            return a - b;
        });
        int n = vals.length;
        UnionFind uf = new UnionFind(n);
        uf.init(vals);
        int res = n;
        for (int[] e : edges) {
            int a = e[0], b = e[1];
            int v = Math.max(vals[a], vals[b]);
            res += uf.merge(a, b);
        }
        return res;
    }
}
class UnionFind {
    int[] fa;
    int[] size;
    int[] max;
    int n;
    UnionFind(int n) {
        this.n = n;
        fa = new int[n];
        for (int i = 0; i < n; i++)
            fa[i] = i;
        max = new int[n];
        size = new int[n];
    }
    void init(int[] a) {
        for (int i = 0; i < a.length; i++) {
            max[i] = a[i];
            size[i] = 1;
        }
    }
    int merge(int a, int b) {
        int pa = find(a), pb = find(b);
        int res = max[pa] == max[pb] ? size[pa] * size[pb] : 0;
        fa[pa] = pb;
        if (max[pa] == max[pb]) {
            size[pb] += size[pa];
        } else if (max[pa] > max[pb]) {
            size[pb] = size[pa];
            max[pb] = max[pa];
        }
        return res;
    }
    int find(int x) {
        return fa[x] == x ? x : (fa[x] = find(fa[x]));
    }
}