
又刷新最好成绩了,Nice!
t4wrong了一次是因为边界情况忘考虑了,在边界只能向左或向右
2103. 环和杆
总计有 n 个环,环的颜色可以是红、绿、蓝中的一种。这些环分布穿在 10 根编号为 0 到 9 的杆上。
给你一个长度为 2n 的字符串 rings ,表示这 n 个环在杆上的分布。rings 中每两个字符形成一个 颜色位置对 ,用于描述每个环:
- 第 i 对中的 第一个 字符表示第 i 个环的 颜色(’R’、’G’、’B’)。
- 第 i 对中的 第二个 字符表示第 i 个环的 位置,也就是位于哪根杆上(’0’ 到 ‘9’)。
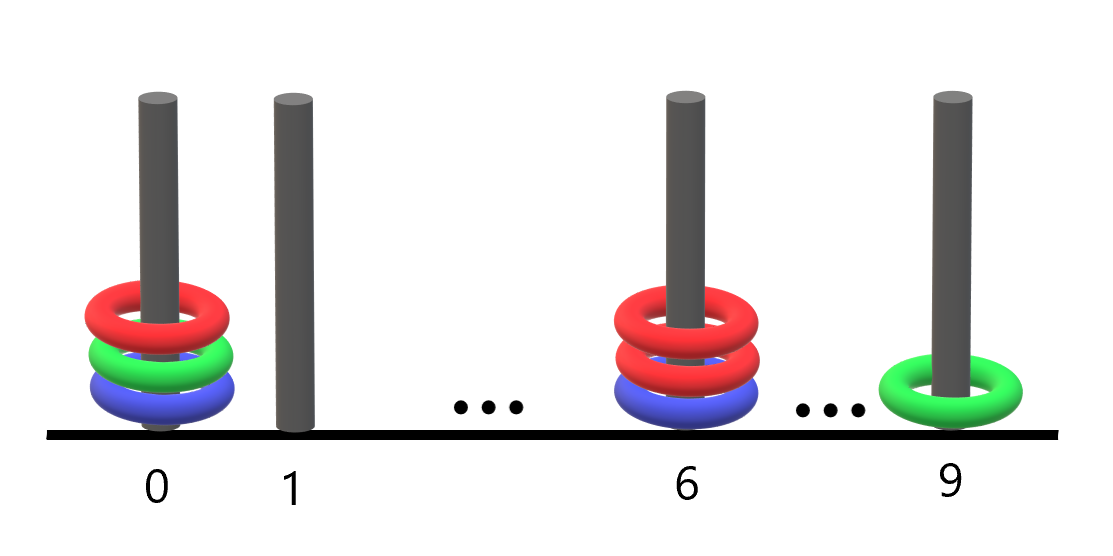
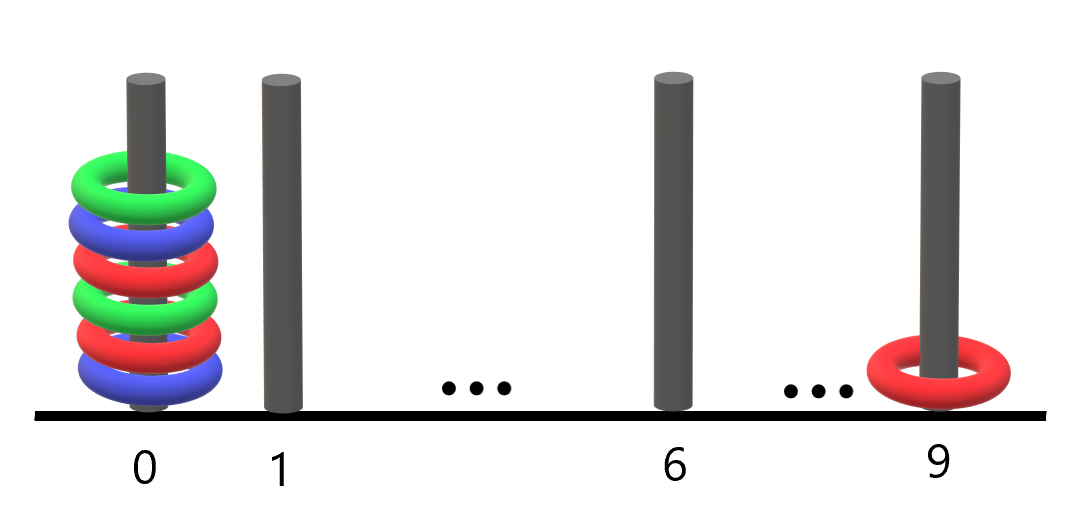
例如,”R3G2B1” 表示:共有 n == 3 个环,红色的环在编号为 3 的杆上,绿色的环在编号为 2 的杆上,蓝色的环在编号为 1 的杆上。
找出所有集齐 全部三种颜色 环的杆,并返回这种杆的数量。
示例 1:
输入:rings = “B0B6G0R6R0R6G9” 输出:1 解释: - 编号 0 的杆上有 3 个环,集齐全部颜色:红、绿、蓝。 - 编号 6 的杆上有 3 个环,但只有红、蓝两种颜色。 - 编号 9 的杆上只有 1 个绿色环。 因此,集齐全部三种颜色环的杆的数目为 1 。
示例 2:
输入:rings = “B0R0G0R9R0B0G0” 输出:1 解释: - 编号 0 的杆上有 6 个环,集齐全部颜色:红、绿、蓝。 - 编号 9 的杆上只有 1 个红色环。 因此,集齐全部三种颜色环的杆的数目为 1 。
示例 3:
输入:rings = “G4” 输出:0 解释: 只给了一个环,因此,不存在集齐全部三种颜色环的杆。
提示:
- rings.length == 2 * n
- 1 <= n <= 100
- 如 i 是 偶数 ,则 rings[i] 的值可以取 ‘R’、’G’ 或 ‘B’(下标从 0 开始计数)
- 如 i 是 奇数 ,则 rings[i] 的值可以取 ‘0’ 到 ‘9’ 中的一个数字(下标从 0 开始计数)
思路:
哈希表
class Solution {public int countPoints(String s) {Map<Integer, Set<Character>> map = new HashMap<>();for (int i = 0; i < s.length(); i += 2) {int a = s.charAt(i + 1) - '0';char b = s.charAt(i);map.computeIfAbsent(a, key -> new HashSet<>()).add(b);}int cnt = 0;for (int x : map.keySet()) {if (map.get(x).size() == 3)cnt++;}return cnt;}}
2104. 子数组范围和
给你一个整数数组 nums 。nums 中,子数组的 范围 是子数组中最大元素和最小元素的差值。
返回 nums 中 所有 子数组范围的 和 。
子数组是数组中一个连续 非空 的元素序列。
示例 1:
输入:nums = [1,2,3] 输出:4 解释:nums 的 6 个子数组如下所示: [1],范围 = 最大 - 最小 = 1 - 1 = 0 [2],范围 = 2 - 2 = 0 [3],范围 = 3 - 3 = 0 [1,2],范围 = 2 - 1 = 1 [2,3],范围 = 3 - 2 = 1 [1,2,3],范围 = 3 - 1 = 2 所有范围的和是 0 + 0 + 0 + 1 + 1 + 2 = 4
示例 2:
输入:nums = [1,3,3] 输出:4 解释:nums 的 6 个子数组如下所示: [1],范围 = 最大 - 最小 = 1 - 1 = 0 [3],范围 = 3 - 3 = 0 [3],范围 = 3 - 3 = 0 [1,3],范围 = 3 - 1 = 2 [3,3],范围 = 3 - 3 = 0 [1,3,3],范围 = 3 - 1 = 2 所有范围的和是 0 + 0 + 0 + 2 + 0 + 2 = 4
示例 3:
输入:nums = [4,-2,-3,4,1] 输出:59 解释:nums 中所有子数组范围的和是 59
提示:
1 <= nums.length <= 1000-109 <= nums[i] <= 109
思路:
方法一:遍历子数组起点 + 双指针
class Solution {public long subArrayRanges(int[] nums) {long res = 0;for (int i = 0; i < nums.length; i++) {long max = nums[i], min = nums[i];for (int j = i + 1; j < nums.length; j++) {max = Math.max(nums[j], max);min = Math.min(nums[j], min);res += max - min;}}return res;}}
方法二:单调栈,一段区间 最大值-最小值,分开考虑最大值与最小值,
拿最大值来说,考虑当前元素,找到其左边第一个大于它的元素或边界,找到其右边大于等于它的第一个元素或者边界。
使用组合计算出当前元素作为最大值出现的所有连续子数组的个数,res += cnt * nums[i]
最小值同理res -= cnt * nums[i]
这里一边大于,另一边大于等于是为了不出现重复区间。
class Solution {public long subArrayRanges(int[] nums) {long res = 0;Deque<Integer> smin = new LinkedList<>();Deque<Integer> smax = new LinkedList<>();for (int i = 0; i < nums.length; i++) {while (!smin.isEmpty() && nums[smin.peek()] <= nums[i]) {int j = smin.pop();int l = smin.isEmpty() ? -1 : smin.peek();res += 1L * (i - j) * (j - l) * nums[j];}smin.push(i);while (!smax.isEmpty() && nums[smax.peek()] >= nums[i]) {int j = smax.pop();int l = smax.isEmpty() ? -1 : smax.peek();res -= 1L * (i - j) * (j - l) * nums[j];}smax.push(i);}int r = nums.length;while (!smin.isEmpty()) {int j = smin.pop();int l = smin.isEmpty() ? -1 : smin.peek();res += 1L * (r - j) * (j - l) * nums[j];}while (!smax.isEmpty()) {int j = smax.pop();int l = smax.isEmpty() ? -1 : smax.peek();res -= 1L * (r - j) * (j - l) * nums[j];}return res;}}
2105. 给植物浇水 II
Alice 和 Bob 打算给花园里的 n 株植物浇水。植物排成一行,从左到右进行标记,编号从 0 到 n - 1 。其中,第 i 株植物的位置是 x = i 。
每一株植物都需要浇特定量的水。Alice 和 Bob 每人有一个水罐,最初是满的 。他们按下面描述的方式完成浇水:
- Alice 按 从左到右 的顺序给植物浇水,从植物 0 开始。Bob 按 从右到左 的顺序给植物浇水,从植物 n - 1 开始。他们 同时 给植物浇水。
- 如果没有足够的水 完全 浇灌下一株植物,他 / 她会立即重新灌满浇水罐。
- 不管植物需要多少水,浇水所耗费的时间都是一样的。
- 不能 提前重新灌满水罐。
- 每株植物都可以由 Alice 或者 Bob 来浇水。
- 如果 Alice 和 Bob 到达同一株植物,那么当前水罐中水更多的人会给这株植物浇水。如果他俩水量相同,那么 Alice 会给这株植物浇水。
给你一个下标从 0 开始的整数数组 plants ,数组由 n 个整数组成。其中,plants[i] 为第 i 株植物需要的水量。另有两个整数 capacityA 和 capacityB 分别表示 Alice 和 Bob 水罐的容量。返回两人浇灌所有植物过程中重新灌满水罐的 次数 。
示例 1:
输入:plants = [2,2,3,3], capacityA = 5, capacityB = 5 输出:1 解释: - 最初,Alice 和 Bob 的水罐中各有 5 单元水。 - Alice 给植物 0 浇水,Bob 给植物 3 浇水。 - Alice 和 Bob 现在分别剩下 3 单元和 2 单元水。 - Alice 有足够的水给植物 1 ,所以她直接浇水。Bob 的水不够给植物 2 ,所以他先重新装满水,再浇水。 所以,两人浇灌所有植物过程中重新灌满水罐的次数 = 0 + 0 + 1 + 0 = 1 。
示例 2:
输入:plants = [2,2,3,3], capacityA = 3, capacityB = 4 输出:2 解释: - 最初,Alice 的水罐中有 3 单元水,Bob 的水罐中有 4 单元水。 - Alice 给植物 0 浇水,Bob 给植物 3 浇水。 - Alice 和 Bob 现在都只有 1 单元水,并分别需要给植物 1 和植物 2 浇水。 - 由于他们的水量均不足以浇水,所以他们重新灌满水罐再进行浇水。 所以,两人浇灌所有植物过程中重新灌满水罐的次数 = 0 + 1 + 1 + 0 = 2 。
示例 3:
输入:plants = [5], capacityA = 10, capacityB = 8 输出:0 解释: - 只有一株植物 - Alice 的水罐有 10 单元水,Bob 的水罐有 8 单元水。因此 Alice 的水罐中水更多,她会给这株植物浇水。 所以,两人浇灌所有植物过程中重新灌满水罐的次数 = 0 。
示例 4:
输入:plants = [1,2,4,4,5], capacityA = 6, capacityB = 5 输出:2 解释: - 最初,Alice 的水罐中有 6 单元水,Bob 的水罐中有 5 单元水。 - Alice 给植物 0 浇水,Bob 给植物 4 浇水。 - Alice 和 Bob 现在分别剩下 5 单元和 0 单元水。 - Alice 有足够的水给植物 1 ,所以她直接浇水。Bob 的水不够给植物 3 ,所以他先重新装满水,再浇水。 - Alice 和 Bob 现在分别剩下 3 单元和 1 单元水。 - 由于 Alice 的水更多,所以由她给植物 2 浇水。然而,她水罐里的水不够给植物 2 ,所以她先重新装满水,再浇水。 所以,两人浇灌所有植物过程中重新灌满水罐的次数 = 0 + 0 + 1 + 1 + 0 = 2 。
示例 5:
输入:plants = [2,2,5,2,2], capacityA = 5, capacityB = 5 输出:1 解释: Alice 和 Bob 都会到达中间的植物,并且此时他俩剩下的水量相同,所以 Alice 会给这株植物浇水。 由于她到达时只剩下 1 单元水,所以需要重新灌满水罐。 这是唯一一次需要重新灌满水罐的情况。所以,两人浇灌所有植物过程中重新灌满水罐的次数 = 1 。
提示:
n == plants.length1 <= n <= 1051 <= plants[i] <= 106max(plants[i]) <= capacityA, capacityB <= 109
思路:这题过于简单了,和第一题水平差不多。
class Solution {public int minimumRefill(int[] p, int ca, int cb) {int n = p.length;if (n % 2 == 0) {int k = n / 2;int cnt = 0;int A = ca, B = cb;for (int i = 0; i < k; i++) {if (ca >= p[i]) {ca -= p[i];} else {ca = A - p[i];cnt++;}}for (int i = n - 1; i >= k; i--) {if (cb >= p[i]) {cb -= p[i];} else {cb = B - p[i];cnt++;}}return cnt;} else {int k = n / 2;int cnt = 0;int A = ca, B = cb;for (int i = 0; i < k; i++) {if (ca >= p[i]) {ca -= p[i];} else {ca = A - p[i];cnt++;}}for (int i = n - 1; i > k; i--) {if (cb >= p[i]) {cb -= p[i];} else {cb = B - p[i];cnt++;}}int max = Math.max(ca, cb);if (max < p[k]) cnt++;return cnt;}}}
2106. 摘水果
在一个无限的 x 坐标轴上,有许多水果分布在其中某些位置。给你一个二维整数数组 fruits ,其中 fruits[i] = [positioni, amounti] 表示共有 amounti 个水果放置在 positioni 上。fruits 已经按 positioni 升序排列 ,每个 positioni 互不相同 。
另给你两个整数 startPos 和 k 。最初,你位于 startPos 。从任何位置,你可以选择 向左或者向右 走。在 x 轴上每移动 一个单位 ,就记作 一步 。你总共可以走 最多 k 步。你每达到一个位置,都会摘掉全部的水果,水果也将从该位置消失(不会再生)。
返回你可以摘到水果的 最大总数 。
示例 1:
输入:fruits = [[2,8],[6,3],[8,6]], startPos = 5, k = 4 输出:9 解释: 最佳路线为: - 向右移动到位置 6 ,摘到 3 个水果 - 向右移动到位置 8 ,摘到 6 个水果 移动 3 步,共摘到 3 + 6 = 9 个水果 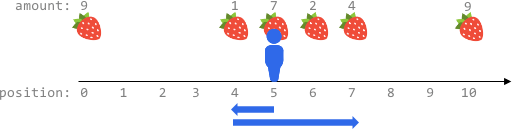
示例 2:
输入:fruits = [[0,9],[4,1],[5,7],[6,2],[7,4],[10,9]], startPos = 5, k = 4 输出:14 解释: 可以移动最多 k = 4 步,所以无法到达位置 0 和位置 10 。 最佳路线为: - 在初始位置 5 ,摘到 7 个水果 - 向左移动到位置 4 ,摘到 1 个水果 - 向右移动到位置 6 ,摘到 2 个水果 - 向右移动到位置 7 ,摘到 4 个水果 移动 1 + 3 = 4 步,共摘到 7 + 1 + 2 + 4 = 14 个水果
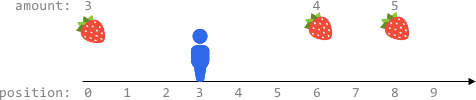
示例 3:
输入:fruits = [[0,3],[6,4],[8,5]], startPos = 3, k = 2 输出:0 解释: 最多可以移动 k = 2 步,无法到达任一有水果的地方
提示:
1 <= fruits.length <= 105fruits[i].length == 20 <= startPos, positioni <= 2 * 105对于任意 i > 0 ,positioni-1 < positioni 均成立(下标从 **0** 开始计数)1 <= amounti <= 1040 <= k <= 2 * 105
思路:
分两种情况,向左走然后向右走或者向右走然后向左走
用二分 + 前缀和 基本就可以了
class Solution {public int maxTotalFruits(int[][] f, int S, int k) {int max = 0;int c1 = 0, c2 = 0;for (int[] p : f) {if (p[0] >= S && p[0] - S <= k)c1 += p[1];if (p[0] <= S && S - p[0] <= k)c2 += p[1];}max = Math.max(c1, c2);Arrays.sort(f, (o1, o2) -> (o1[0] - o2[0]));if (f[0][0] >= S || f[f.length - 1][0] <= S) return max;for (int i = 1; i < f.length; i++) {f[i][1] += f[i - 1][1];}int pos = -1;for (int i = 0; i < f.length; i++) {if (f[i][0] >= S) {pos = i;break;}}// if (pos == -1) return max;int cnt = 0;for (int i = pos; i < f.length; i++) {int x = k - (f[i][0] - S) * 2;if (x >= 0) {x = S - x;cnt = Math.max(cnt, f[i][1] - get(f, x, true));} else {break;}max = Math.max(cnt, max);}// System.out.println(max);for (int i = pos - 1; i >= 0; i--) {int x = k - (S - f[i][0]) * 2;if (x >= 0) {x = S + x;int minus = i == 0 ? 0 : f[i - 1][1];cnt = Math.max(cnt, get(f, x, false) - minus);} else break;max = Math.max(cnt, max);}return max;}int get(int[][] f, int x, boolean d) {int l = 0, r = f.length - 1;if (d) {while (l < r) {int mid = l + r + 1>> 1;if (f[mid][0] >= x)r = mid - 1;elsel = mid;}int begin = f[l][0] < x ? f[l][1] : 0;return begin;} else {while (l < r) {int mid = l + r + 1 >> 1;if (f[mid][0] > x)r = mid - 1;elsel = mid;}return f[l][1];}}}

