
虽然AK了,但t4做的有点问题,如果数据再强一点就有可能过不了!卡太极限了!
5922. 统计出现过一次的公共字符串
给你两个字符串数组 words1 和 words2 ,请你返回在两个字符串数组中 都恰好出现一次 的字符串的数目。
示例 1:
输入:words1 = [“leetcode”,”is”,”amazing”,”as”,”is”], words2 = [“amazing”,”leetcode”,”is”] 输出:2 解释: - “leetcode” 在两个数组中都恰好出现一次,计入答案。 - “amazing” 在两个数组中都恰好出现一次,计入答案。 - “is” 在两个数组中都出现过,但在 words1 中出现了 2 次,不计入答案。 - “as” 在 words1 中出现了一次,但是在 words2 中没有出现过,不计入答案。 所以,有 2 个字符串在两个数组中都恰好出现了一次。
示例 2:
输入:words1 = [“b”,”bb”,”bbb”], words2 = [“a”,”aa”,”aaa”] 输出:0 解释:没有字符串在两个数组中都恰好出现一次。
示例 3:
输入:words1 = [“a”,”ab”], words2 = [“a”,”a”,”a”,”ab”] 输出:1 解释:唯一在两个数组中都出现一次的字符串是 “ab” 。
提示:
- 1 <= words1.length, words2.length <= 1000
- 1 <= words1[i].length, words2[j].length <= 30
- words1[i] 和 words2[j] 都只包含小写英文字母。
思路:
哈希表 + 遍历
class Solution {public int countWords(String[] words1, String[] words2) {Map<String, Integer> m1 = new HashMap<>();Map<String, Integer> m2 = new HashMap<>();for (String s : words1) {m1.merge(s, 1, Integer::sum);}for (String s : words2) {m2.merge(s, 1, Integer::sum);}int res = 0;for (String s : m1.keySet()) {if (m1.get(s) == 1 && m2.getOrDefault(s, 0) == 1)res++;}return res;}}
5923. 从房屋收集雨水需要的最少水桶数
给你一个下标从 0 开始的字符串 street 。street 中每个字符要么是表示房屋的 ‘H’ ,要么是表示空位的 ‘.’ 。
你可以在 空位 放置水桶,从相邻的房屋收集雨水。位置在 i - 1 或者 i + 1 的水桶可以收集位置为 i 处房屋的雨水。一个水桶如果相邻两个位置都有房屋,那么它可以收集 两个 房屋的雨水。
在确保 每个 房屋旁边都 至少 有一个水桶的前提下,请你返回需要的 最少 水桶数。如果无解请返回 -1 。
示例 1:
输入:street = “H..H” 输出:2 解释: 我们可以在下标为 1 和 2 处放水桶。 “H..H” -> “HBBH”(’B’ 表示放置水桶)。 下标为 0 处的房屋右边有水桶,下标为 3 处的房屋左边有水桶。 所以每个房屋旁边都至少有一个水桶收集雨水。
示例 2:
输入:street = “.H.H.” 输出:1 解释: 我们可以在下标为 2 处放置一个水桶。 “.H.H.” -> “.HBH.”(’B’ 表示放置水桶)。 下标为 1 处的房屋右边有水桶,下标为 3 处的房屋左边有水桶。 所以每个房屋旁边都至少有一个水桶收集雨水。
示例 3:
输入:street = “.HHH.” 输出:-1 解释: 没有空位可以放置水桶收集下标为 2 处的雨水。 所以没有办法收集所有房屋的雨水。
示例 4:
输入:street = “H” 输出:-1 解释: 没有空位放置水桶。 所以没有办法收集所有房屋的雨水。
示例 5:
输入:street = “.” 输出:0 解释: 没有房屋需要收集雨水。 所以需要 0 个水桶。
提示:
- 1 <= street.length <= 105
- street[i] 要么是 ‘H’ ,要么是 ‘.’ 。
思路:
贪心,如果一个房子后面能放桶就放后面,但是如果前面已经放了桶就跳过。
class Solution {public int minimumBuckets(String street) {char[] c = street.toCharArray();int n = c.length;int res = 0;for (int i = 0; i < n; i++) {if (c[i] == 'H') {if ((i - 1 < 0 || c[i - 1] == 'H') && (i + 1 >= n || c[i + 1] == 'H'))return -1;if (i - 1 >= 0 && c[i - 1] == '0')continue;if (i + 1 < n && c[i + 1] == '.') {res++;c[i + 1] = '0';} else {c[i - 1] = '0';res++;}}}return res;}}
5924. 网格图中机器人回家的最小代价
给你一个 m x n 的网格图,其中 (0, 0) 是最左上角的格子,(m - 1, n - 1) 是最右下角的格子。给你一个整数数组 startPos ,startPos = [startrow, startcol] 表示 初始 有一个 机器人 在格子 (startrow, startcol) 处。同时给你一个整数数组 homePos ,homePos = [homerow, homecol] 表示机器人的 家 在格子 (homerow, homecol) 处。
机器人需要回家。每一步它可以往四个方向移动:上,下,左,右,同时机器人不能移出边界。每一步移动都有一定代价。再给你两个下标从 0 开始的额整数数组:长度为 m 的数组 rowCosts 和长度为 n 的数组 colCosts 。
- 如果机器人往 上 或者往 下 移动到第 r 行 的格子,那么代价为 rowCosts[r] 。
- 如果机器人往 左 或者往 右 移动到第 c 列 的格子,那么代价为 colCosts[c] 。
请你返回机器人回家需要的 最小总代价 。
示例 1: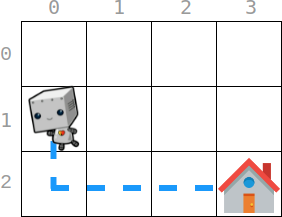
输入:startPos = [1, 0], homePos = [2, 3], rowCosts = [5, 4, 3], colCosts = [8, 2, 6, 7] 输出:18 解释:一个最优路径为: 从 (1, 0) 开始 -> 往下走到 (2, 0) 。代价为 rowCosts[2] = 3 。 -> 往右走到 (2, 1) 。代价为 colCosts[1] = 2 。 -> 往右走到 (2, 2) 。代价为 colCosts[2] = 6 。 -> 往右走到 (2, 3) 。代价为 colCosts[3] = 7 。 总代价为 3 + 2 + 6 + 7 = 18
示例 2:
输入:startPos = [0, 0], homePos = [0, 0], rowCosts = [5], colCosts = [26] 输出:0 解释:机器人已经在家了,所以不需要移动。总代价为 0 。
提示:
m == rowCosts.lengthn == colCosts.length1 <= m, n <= 1050 <= rowCosts[r], colCosts[c] <= 104startPos.length == 2homePos.length == 20 <= startrow, homerow < m0 <= startcol, homecol < n
思路:脑筋急转弯,在不绕路的情况下,无论怎么走,结果都是定值。
class Solution {public int minCost(int[] startPos, int[] homePos, int[] rowCosts, int[] colCosts) {int a = startPos[0], b = homePos[0], x = startPos[1], y = homePos[1];int res = 0;if (a < b) {for (int i = a; i < b; i++)res += rowCosts[i + 1];} else if (a > b) {for (int i = a; i > b; i--)res += rowCosts[i - 1];}if (x < y) {for (int i = x; i < y; i++)res += colCosts[i + 1];} else if (x > y) {for (int i = x; i > y; i--)res += colCosts[i - 1];}return res;}}
5925. 统计农场中肥沃金字塔的数目
有一个 矩形网格 状的农场,划分为 m 行 n 列的单元格。每个格子要么是 肥沃的 (用 1 表示),要么是 贫瘠 的(用 0 表示)。网格图以外的所有与格子都视为贫瘠的。
农场中的 金字塔 区域定义如下:
- 区域内格子数目 大于 1 且所有格子都是 肥沃的 。
- 金字塔 顶端 是这个金字塔 最上方 的格子。金字塔的高度是它所覆盖的行数。令 (r, c) 为金字塔的顶端且高度为 h ,那么金字塔区域内包含的任一格子 (i, j) 需满足 r <= i <= r + h - 1 且 c - (i - r) <= j <= c + (i - r) 。
一个 倒金字塔 类似定义如下:
- 区域内格子数目 大于 1 且所有格子都是 肥沃的 。
- 倒金字塔的 顶端 是这个倒金字塔 最下方 的格子。倒金字塔的高度是它所覆盖的行数。令 (r, c) 为金字塔的顶端且高度为 h ,那么金字塔区域内包含的任一格子 (i, j) 需满足 r - h + 1 <= i <= r 且 c - (r - i) <= j <= c + (r - i) 。
下图展示了部分符合定义和不符合定义的金字塔区域。黑色区域表示肥沃的格子。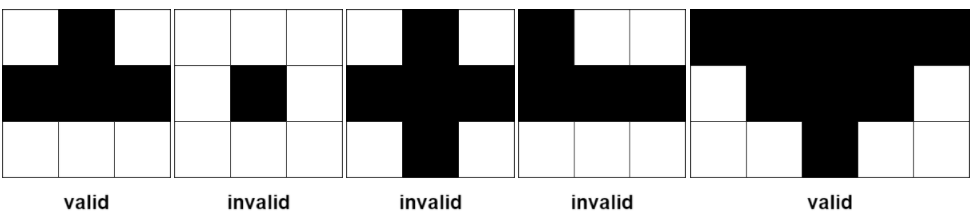
给你一个下标从 0 开始且大小为 m x n 的二进制矩阵 grid ,它表示农场,请你返回 grid 中金字塔和倒金字塔的 总数目 。
示例 1: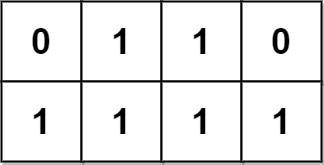
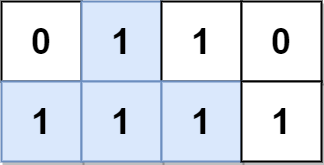
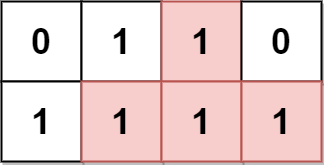
输入:grid = [[0,1,1,0],[1,1,1,1]] 输出:2 解释: 2 个可能的金字塔区域分别如上图蓝色和红色区域所示。 这个网格图中没有倒金字塔区域。 所以金字塔区域总数为 2 + 0 = 2 。
示例 2: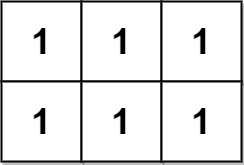
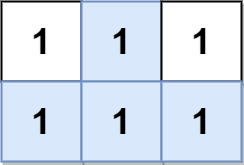
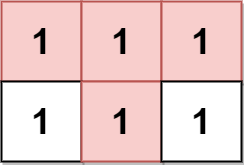
输入:grid = [[1,1,1],[1,1,1]] 输出:2 解释: 金字塔区域如上图蓝色区域所示,倒金字塔如上图红色区域所示。 所以金字塔区域总数目为 1 + 1 = 2 。
示例 3: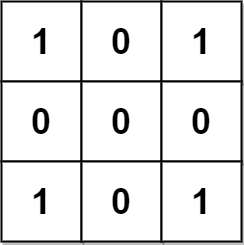
输入:grid = [[1,0,1],[0,0,0],[1,0,1]] 输出:0 解释: 网格图中没有任何金字塔或倒金字塔区域。
示例 4:
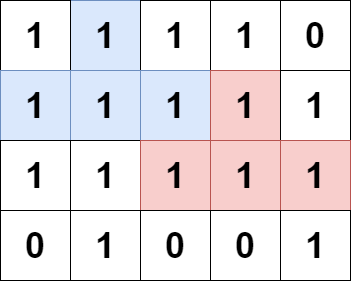
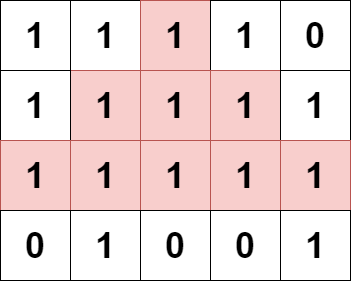
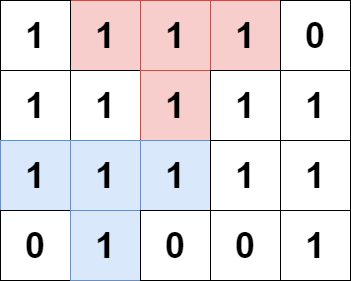
输入:grid = [[1,1,1,1,0],[1,1,1,1,1],[1,1,1,1,1],[0,1,0,0,1]] 输出:13 解释: 有 7 个金字塔区域。上图第二和第三张图中展示了它们中的 3 个。 有 6 个倒金字塔区域。上图中最后一张图展示了它们中的 2 个。 所以金字塔区域总数目为 7 + 6 = 13.
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 10001 <= m * n <= 105grid[i][j] 要么是 0 ,要么是 1 。
思路:
比赛时的方法:
计算每一行的前缀和。O(nm)
暴力统计每个点作为塔顶的金字塔个数,一次遍历(每个点的时间复杂度为O(n))就可以求出正金字塔和倒金字塔。 O(n m * n)
总时间复杂度正好是108,太极限了。
正解:DP
状态表示:f[i][j]表示(i, j)为塔尖的金字塔的层数x,这样以(i, j)为塔尖的可组成的金字塔个数为x - 1。
状态转移:f[i][j] = Math.min(f[i + 1][j - 1], f[i + 1][j + 1]) + 1 且必须满足g[i + 1][j] == 1
从下往上遍历,这样可以求出正金字塔的个数。
逆金字塔的个数相当于把整个数组上下反转一下,DP再来一次。
class Solution {int n, m;public int countPyramids(int[][] g) {n = g.length; m = g[0].length;int res = get(g);//反转数组for (int i = 0, j = n - 1; i < j; i++, j--) {for (int k = 0; k < m; k++) {int x = g[i][k];g[i][k] = g[j][k];g[j][k] = x;}}res += get(g);return res;}int get(int[][] g) {int res = 0;int[][] f = new int[n][m];for (int i = n - 1; i >= 0; i--) {for (int j = 0; j < m; j++) {if (g[i][j] == 1)f[i][j] = 1;elsecontinue;if (i + 1 < n && g[i + 1][j] == 1) {int min = 0x3f3f3f3f;if (j - 1 >= 0 && j + 1 < m)min = Math.min(f[i + 1][j - 1], f[i + 1][j + 1]);f[i][j] += min == 0x3f3f3f3f ? 0 : min;}res += Math.max(f[i][j] - 1, 0);}}return res;}}

