94. 二叉树的中序遍历

给定一个二叉树的根节点 root ，返回它的 中序 遍历。

示例 1：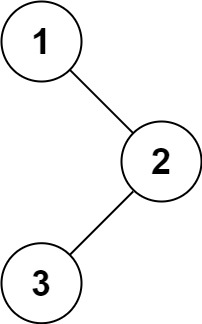
中序遍历 - 图1
输入：root = [1,null,2,3]
输出：[1,3,2]

示例 2：
输入：root = []
输出：[]

示例 3：
输入：root = [1]
输出：[1]

示例 4：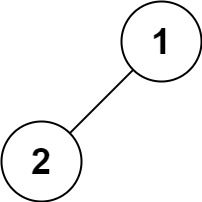
中序遍历 - 图2
输入：root = [1,2]
输出：[2,1]

示例 5：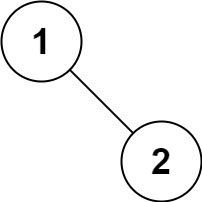
中序遍历 - 图3
输入：root = [1,null,2]
输出：[1,2]


提示：

  • 树中节点数目在范围 [0, 100] 内

  • -100 <= Node.val <= 100


    进阶: 递归算法很简单，你可以通过迭代算法完成吗？

    递归

  1. /**
  2.  * Definition for a binary tree node.
  3.  * public class TreeNode {
  4.  *     int val;
  5.  *     TreeNode left;
  6.  *     TreeNode right;
  7.  *     TreeNode() {}
  8.  *     TreeNode(int val) { this.val = val; }
  9.  *     TreeNode(int val, TreeNode left, TreeNode right) {
  10.  *         this.val = val;
  11.  *         this.left = left;
  12.  *         this.right = right;
  13.  *     }
  14.  * }
  15.  */
  16. class Solution {
  17.     List<Integer> res = new ArrayList<>();
  18.     public List<Integer> inorderTraversal(TreeNode root) {
  19.         dfs(root);
  20.         return res;
  21.     }
  22.     void dfs(TreeNode root) {
  23.         if (root == null)
  24.             return;
  25.         dfs(root.left);
  26.         res.add(root.val);
  27.         dfs(root.right);
  28.     }
  29. }

迭代

  1. class Solution {
  2.     public List<Integer> inorderTraversal(TreeNode root) {
  3.         List<Integer> res = new ArrayList<>();
  4.         if (root == null)
  5.             return res;
  6.         Deque<TreeNode> stack = new LinkedList<>();
  8.         while (root != null || !stack.isEmpty()) {
  9.             while (root != null) {
  10.                 stack.push(root);
  11.                 root = root.left;
  12.             }
  13.             root = stack.pop();
  14.             res.add(root.val);
  15.             root = root.right;
  16.         }
  17.         return res;
  18.     }
  19. }

Morris中序遍历

中序遍历 - 图4

从根节点开始遍历，直至当前节点为空为止：

  1. 如果当前节点没有左儿子，则打印当前节点的值，然后进入右子树；
  2. 如果当前节点有左儿子，则找当前节点的前驱。

(1) 如果前驱节点的右儿子为空，说明左子树没遍历过，则进入左子树遍历，并将前驱节点的右儿子置成当前节点，方便回溯；
(2) 如果前驱节点的右儿子为当前节点，说明左子树已被遍历过，则将前驱节点的右儿子恢复为空，然后打印当前节点的值，然后进入右子树继续遍历；

  1. class Solution {
  2.     public List<Integer> inorderTraversal(TreeNode root) {
  3.         List<Integer> res = new ArrayList<>();
  5.         while (root != null) {
  6.             if (root.left == null) {
  7.                 res.add(root.val);
  8.                 root = root.right;
  9.             } else {
  10.                 TreeNode pre = root.left;
  11.                 while (pre.right != null && pre.right != root)
  12.                     pre = pre.right;
  13.                 if (pre.right == null) {
  14.                     pre.right = root;
  15.                     root = root.left;
  16.                 } else {
  17.                     pre.right = null;
  18.                     res.add(root.val);
  19.                     root = root.right;
  20.                 }
  21.             }
  22.         }
  23.         return res;
  24.     }
  25. }

Morris-traversal算法的时间复杂度是 O(n)，额外空间复杂度是 O(1)。