5926. 买票需要的时间
有 n 个人前来排队买票,其中第 0 人站在队伍 最前方 ,第 (n - 1) 人站在队伍 最后方 。
给你一个下标从 0 开始的整数数组 tickets ,数组长度为 n ,其中第 i 人想要购买的票数为 tickets[i] 。
每个人买票都需要用掉 恰好 1 秒 。一个人 一次只能买一张票 ,如果需要购买更多票,他必须走到 队尾 重新排队(瞬间 发生,不计时间)。如果一个人没有剩下需要买的票,那他将会 离开 队伍。
返回位于位置 k(下标从 0 开始)的人完成买票需要的时间(以秒为单位)。
示例 1:
输入:tickets = [2,3,2], k = 2
输出:6
解释:
- 第一轮,队伍中的每个人都买到一张票,队伍变为 [1, 2, 1] 。
- 第二轮,队伍中的每个都又都买到一张票,队伍变为 [0, 1, 0] 。
位置 2 的人成功买到 2 张票,用掉 3 + 3 = 6 秒。
示例 2:
输入:tickets = [5,1,1,1], k = 0
输出:8
解释:
- 第一轮,队伍中的每个人都买到一张票,队伍变为 [4, 0, 0, 0] 。
- 接下来的 4 轮,只有位置 0 的人在买票。
位置 0 的人成功买到 5 张票,用掉 4 + 1 + 1 + 1 + 1 = 8 秒。
提示:
n == tickets.length1 <= n <= 1001 <= tickets[i] <= 1000 <= k < n
思路:
简单的模拟题,买票,买票,买票。
class Solution {public int timeRequiredToBuy(int[] tickets, int k) {int res = 0;while (tickets[k] > 0) {for (int i = 0; i < tickets.length; i++) {if (tickets[i] > 0) {tickets[i]--;res++;}if (i == k && tickets[k] == 0)break;}}return res;}}
5927. 反转偶数长度组的节点
给你一个链表的头节点 head 。
链表中的节点 按顺序 划分成若干 非空 组,这些非空组的长度构成一个自然数序列(1, 2, 3, 4, ...)。一个组的 长度 就是组中分配到的节点数目。换句话说:
- 节点
1分配给第一组 - 节点
2和3分配给第二组 - 节点
4、5和6分配给第三组,以此类推
注意,最后一组的长度可能小于或者等于 1 + 倒数第二组的长度 。
反转 每个 偶数 长度组中的节点,并返回修改后链表的头节点 head 。
示例 1:
输入:head = [5,2,6,3,9,1,7,3,8,4]
输出:[5,6,2,3,9,1,4,8,3,7]
解释:
- 第一组长度为 1 ,奇数,没有发生反转。
- 第二组长度为 2 ,偶数,节点反转。
- 第三组长度为 3 ,奇数,没有发生反转。
- 最后一组长度为 4 ,偶数,节点反转。
示例 2: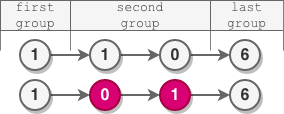
输入:head = [1,1,0,6]
输出:[1,0,1,6]
解释:
- 第一组长度为 1 ,没有发生反转。
- 第二组长度为 2 ,节点反转。
- 最后一组长度为 1 ,没有发生反转。
示例 3: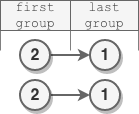
输入:head = [2,1]
输出:[2,1]
解释:
- 第一组长度为 1 ,没有发生反转。
- 最后一组长度为 1 ,没有发生反转。
示例 4:
输入:head = [8]
输出:[8]
解释:只有一个长度为 1 的组,没有发生反转。
提示:
- 链表中节点数目范围是
[1, 10] 0 <= Node.val <= 10
思路:
比赛的时候是直接在链表上处理的,边界真恶心!
其实可以用数组的。。。
注意:题目中的高亮部分,若最后一段也是偶数个元素的话也需要反转!
/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode() {}* ListNode(int val) { this.val = val; }* ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/class Solution {public ListNode reverseEvenLengthGroups(ListNode head) {if (head == null || head.next == null)return head;ListNode p = head;int cnt = 2;while (p != null) {ListNode cur = p;int len = 0;while (len < cnt && cur.next != null) {len++;cur = cur.next;}if (len < cnt) {if (len > 0 && len % 2 == 0)p.next = reverse(p.next, null);break;}ListNode ne = cur.next, end = p.next;if (cnt % 2 == 0) {p.next = reverse(p.next, ne);end.next = ne;p = end;} else {p = cur;}cnt++;}return head;}ListNode reverse(ListNode head, ListNode end) {if (head.next == end)return head;ListNode newHead = reverse(head.next, end);head.next.next = head;head.next = null;return newHead;}}
//数组实现/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode() {}* ListNode(int val) { this.val = val; }* ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/class Solution {public ListNode reverseEvenLengthGroups(ListNode head) {if (head == null)return head;List<ListNode> list = new ArrayList<>();ListNode p = head;while (p != null) {list.add(p);p = p.next;}int len = 1;for (int i = 0; i < list.size(); i++) {int j = i;while (j + 1 < list.size() && j - i + 1 < len) {j++;}if ((j - i + 1) % 2 == 0)reverse(list, i, j);i = j;len++;}ListNode dummy = new ListNode(-1);p = dummy;for (int i = 0; i < list.size(); i++) {p.next = list.get(i);p = p.next;}p.next = null;return dummy.next;}void reverse(List<ListNode> list, int l, int r) {while (l < r) {// int t = list.get(l).val;// list.get(l).val = list.get(r).val;// list.get(r).val = t;ListNode t = list.get(l);list.set(l, list.get(r));list.set(r, t);l++;r--;}}}
5928. 解码斜向换位密码
难度中等1收藏分享切换为英文接收动态反馈
字符串 originalText 使用 斜向换位密码 ,经由 行数固定 为 rows 的矩阵辅助,加密得到一个字符串 encodedText 。originalText 先按从左上到右下的方式放置到矩阵中。
先填充蓝色单元格,接着是红色单元格,然后是黄色单元格,以此类推,直到到达 originalText 末尾。箭头指示顺序即为单元格填充顺序。所有空单元格用 ' ' 进行填充。矩阵的列数需满足:用 originalText 填充之后,最右侧列 不为空 。
接着按行将字符附加到矩阵中,构造 encodedText 。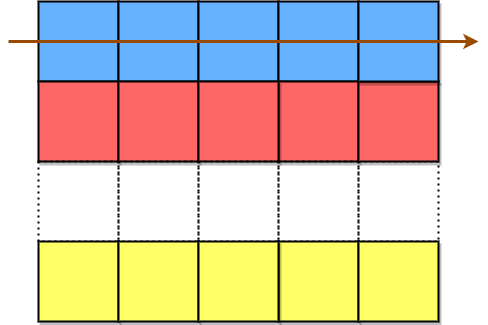
先把蓝色单元格中的字符附加到 encodedText 中,接着是红色单元格,最后是黄色单元格。箭头指示单元格访问顺序。
例如,如果 originalText = "cipher" 且 rows = 3 ,那么我们可以按下述方法将其编码: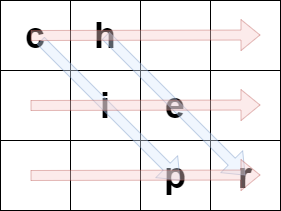
蓝色箭头标识 originalText 是如何放入矩阵中的,红色箭头标识形成 encodedText 的顺序。在上述例子中,encodedText = "ch ie pr" 。
给你编码后的字符串 encodedText 和矩阵的行数 rows ,返回源字符串 originalText 。
注意:originalText 不 含任何尾随空格 ' ' 。生成的测试用例满足 仅存在一个 可能的 originalText 。
示例 1:
输入:encodedText = “ch ie pr”, rows = 3
输出:“cipher”
解释:此示例与问题描述中的例子相同。
示例 2: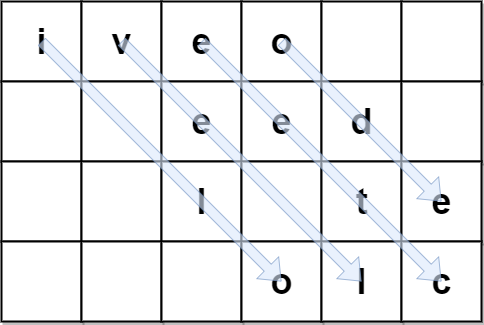
输入:encodedText = “iveo eed l te olc”, rows = 4
输出:“i love leetcode”
解释:上图标识用于编码 originalText 的矩阵。
蓝色箭头展示如何从 encodedText 找到 originalText 。
示例 3:
输入:encodedText = “coding”, rows = 1
输出:“coding”
解释:由于只有 1 行,所以 originalText 和 encodedText 是相同的。
示例 4: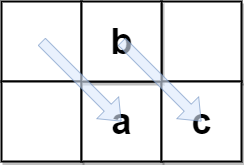
输入:encodedText = “ b ac”, rows = 2
输出:“ abc”
解释:originalText 不能含尾随空格,但它可能会有一个或者多个前置空格。
提示:
0 <= encodedText.length <= 10encodedText仅由小写英文字母和' '组成encodedText是对某个 不含 尾随空格的originalText的一个有效编码1 <= rows <= 1000- 生成的测试用例满足 仅存在一个 可能的
originalText
思路:直接模拟即可
class Solution {public String decodeCiphertext(String e, int rows) {int cols = e.length() / rows;StringBuilder sb = new StringBuilder();for (int i = 0; i < cols; i++) {int k = 0, j = i;while (k < rows && j < cols) {int idx = k * cols + j;sb.append(e.charAt(idx));k++;j++;}}while (sb.length() > 0 && sb.charAt(sb.length() - 1) == ' ')sb.deleteCharAt(sb.length() - 1);return sb.toString();}}
5929. 处理含限制条件的好友请求
给你一个整数 n ,表示网络上的用户数目。每个用户按从 0 到 n - 1 进行编号。
给你一个下标从 0 开始的二维整数数组 restrictions ,其中 restrictions[i] = [x, y] 意味着用户 x 和用户 y 不能 成为 朋友 ,不管是 直接 还是通过其他用户 间接 。
最初,用户里没有人是其他用户的朋友。给你一个下标从 0 开始的二维整数数组 requests 表示好友请求的列表,其中 requests[j] = [u, v] 是用户 u 和用户 v 之间的一条好友请求。
如果 u 和 v 可以成为 朋友 ,那么好友请求将会 成功 。每个好友请求都会按列表中给出的顺序进行处理(即,requests[j] 会在 requests[j + 1] 前)。一旦请求成功,那么对所有未来的好友请求而言, u 和 v 将会 成为直接朋友 。
返回一个 布尔数组 result ,其中元素遵循此规则:如果第 j 个好友请求 成功 ,那么 result[j] 就是 true ;否则,为 false 。
注意:如果 u 和 v 已经是直接朋友,那么他们之间的请求将仍然 成功 。
示例 1:
输入:n = 3, restrictions = [[0,1]], requests = [[0,2],[2,1]]
输出:[true,false]
解释:
请求 0 :用户 0 和 用户 2 可以成为朋友,所以他们成为直接朋友。
请求 1 :用户 2 和 用户 1 不能成为朋友,因为这会使 用户 0 和 用户 1 成为间接朋友 (1—2—0) 。
示例 2:
输入:n = 3, restrictions = [[0,1]], requests = [[1,2],[0,2]]
输出:[true,false]
解释:
请求 0 :用户 1 和 用户 2 可以成为朋友,所以他们成为直接朋友。
请求 1 :用户 0 和 用户 2 不能成为朋友,因为这会使 用户 0 和 用户 1 成为间接朋友 (0—2—1) 。
示例 3:
输入:n = 5, restrictions = [[0,1],[1,2],[2,3]], requests = [[0,4],[1,2],[3,1],[3,4]]
输出:[true,false,true,false]
解释:
请求 0 :用户 0 和 用户 4 可以成为朋友,所以他们成为直接朋友。
请求 1 :用户 1 和 用户 2 不能成为朋友,因为他们之间存在限制。
请求 2 :用户 3 和 用户 1 可以成为朋友,所以他们成为直接朋友。
请求 3 :用户 3 和 用户 4 不能成为朋友,因为这会使 用户 0 和 用户 1 成为间接朋友 (0—4—3—1) 。
提示:
2 <= n <= 10000 <= restrictions.length <= 1000restrictions[i].length == 20 <= x, y <= n - 1x != y1 <= requests.length <= 1000requests[j].length == 20 <= u, v <= n - 1u != v
思路:
并查集
将每对限制用哈希表维护
处理每一个请求
- 求两个人的根节点,若相同说明已经是一组,若不相同,用根节点的邻接域判断两个集合中的人是否有冲突,有冲突说明不能合并,否则可以合并,将人少的合并到人多的集合
class Solution {int[] fa;public boolean[] friendRequests(int n, int[][] restrictions, int[][] requests) {Map<Integer, Set<Integer>> map = new HashMap<>();for (int i = 0; i < n; i++)map.put(i, new HashSet<>());for (int[] p : restrictions) {map.get(p[0]).add(p[1]);map.get(p[1]).add(p[0]);}fa = new int[n];Set<Integer>[] set = new HashSet[n];for (int i = 0; i < n; i++) {fa[i] = i;set[i] = new HashSet<>();set[i].add(i);}boolean[] res = new boolean[requests.length];int idx = 0;label: for (int[] p : requests) {int pa = find(p[0]), pb = find(p[1]);if (pa == pb) {res[idx++] = true;continue;}for (int x : set[pa]) {for (int y : set[pb]) {if (map.get(x).contains(y)) {idx++;continue label;}}}if (set[pa].size() > set[pb].size()) {fa[pb] = pa;set[pa].addAll(set[pb]);} else {fa[pa] = pb;set[pb].addAll(set[pa]);}res[idx] = true;idx++;}return res;}int find(int x) {return x == fa[x] ? x : (fa[x] = find(fa[x]));}}

