1. 介绍
最早被发明的自平衡二叉搜索树。
性质:
- 可以是空树
- 若不是空树,任一节点对应的两棵子树的最大高度差不超过1,因此它也被称为高度平衡树。
查找,插入和删除操作在平均和最坏情况下的时间复杂度都是 O(logn)
增加和删除元素的操作可能需要借由一次或多次的树旋转,以实现树的重新平衡。
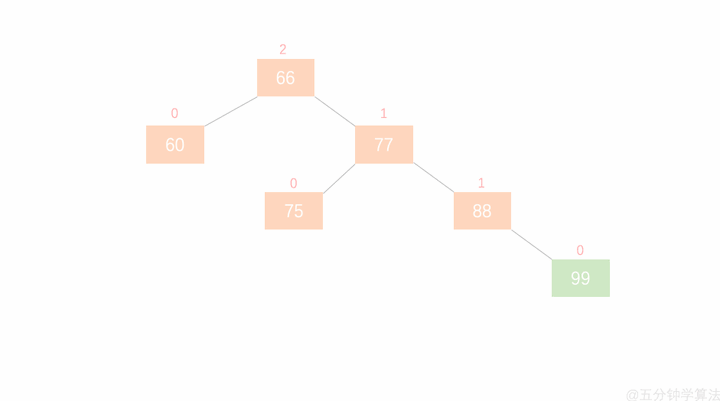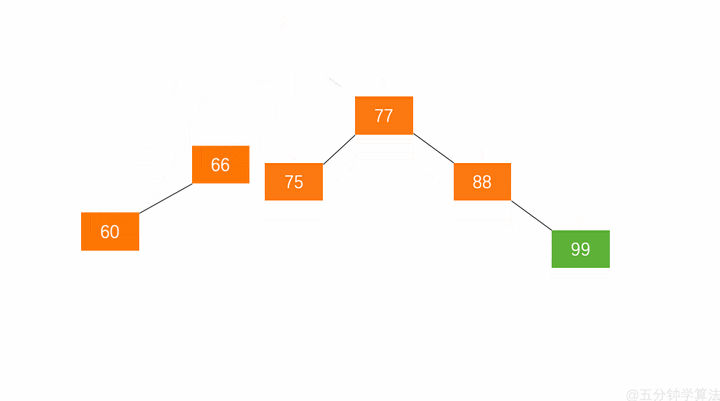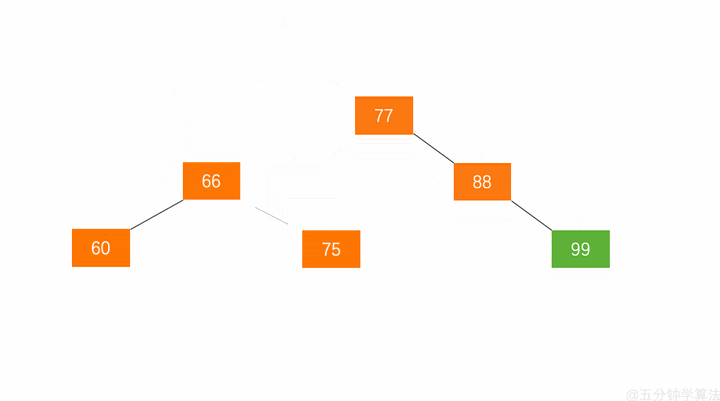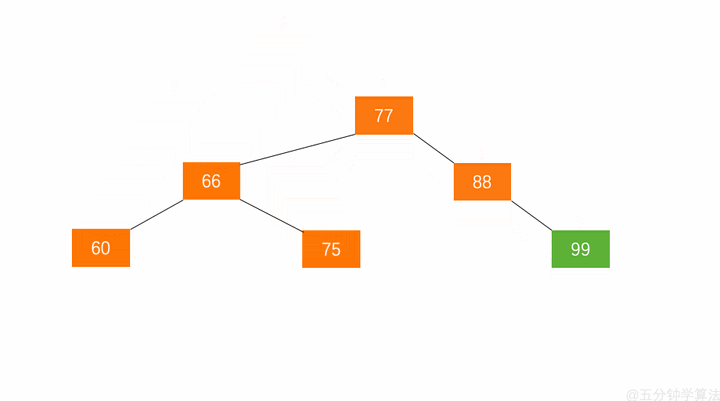
2. 平衡因子
节点的平衡因子
指它的左子树的高度减去它的右子树的高度(有时相反)。带有平衡因子1、0或 -1的节点被认为是平衡的。
带有平衡因子 -2或2的节点被认为是不平衡的,并需要重新平衡这个树。平衡因子可以直接存储在每个节点中,或从可能存储在节点中的子树高度计算出来。
3. 节点结构
class AVL {class Node {int depth;ElementType val;Node left, right, parent;Node(int depth) {this.depth = depth;}}Node root;}
左旋与右旋
最小失衡树:
在新插入的结点向上查找,以第一个平衡因子的绝对值超过 1 的结点为根的子树称为最小不平衡子树。
也就是说,一棵失衡的树,是有可能有多棵子树同时失衡的。而这个时候,我们只要调整最小的不平衡子树,就能够将不平衡的树调整为平衡的树。
平衡二叉树的失衡调整主要是通过旋转最小失衡子树来实现的。根据旋转的方向有两种处理方式,左旋 与 右旋 。
四种插入方式
| 插入方式 | 描述 | 旋转方式 |
|---|---|---|
| LL | 在 A 的左子树根节点的左子树上插入节点而破坏平衡 | 右旋转 |
| RR | 在 A 的右子树根节点的右子树上插入节点而破坏平衡 | 左旋 |
| LR | 在A的左子树根节点的右子树上插入节点而破坏平衡 | 先左旋后右旋 |
| RL | 在 A 的右子树根节点的左子树上插入节点而破坏平衡 | 先右旋后左旋 |
LL

RR
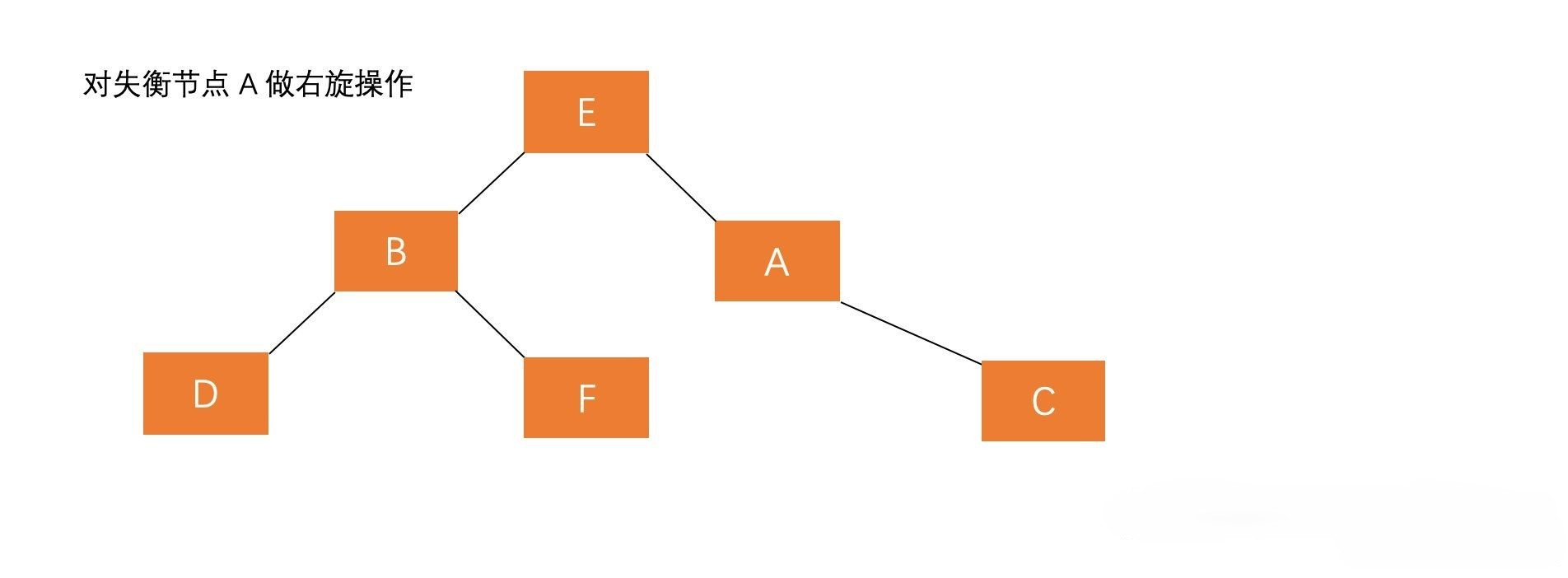
LR
- F为新插入节点
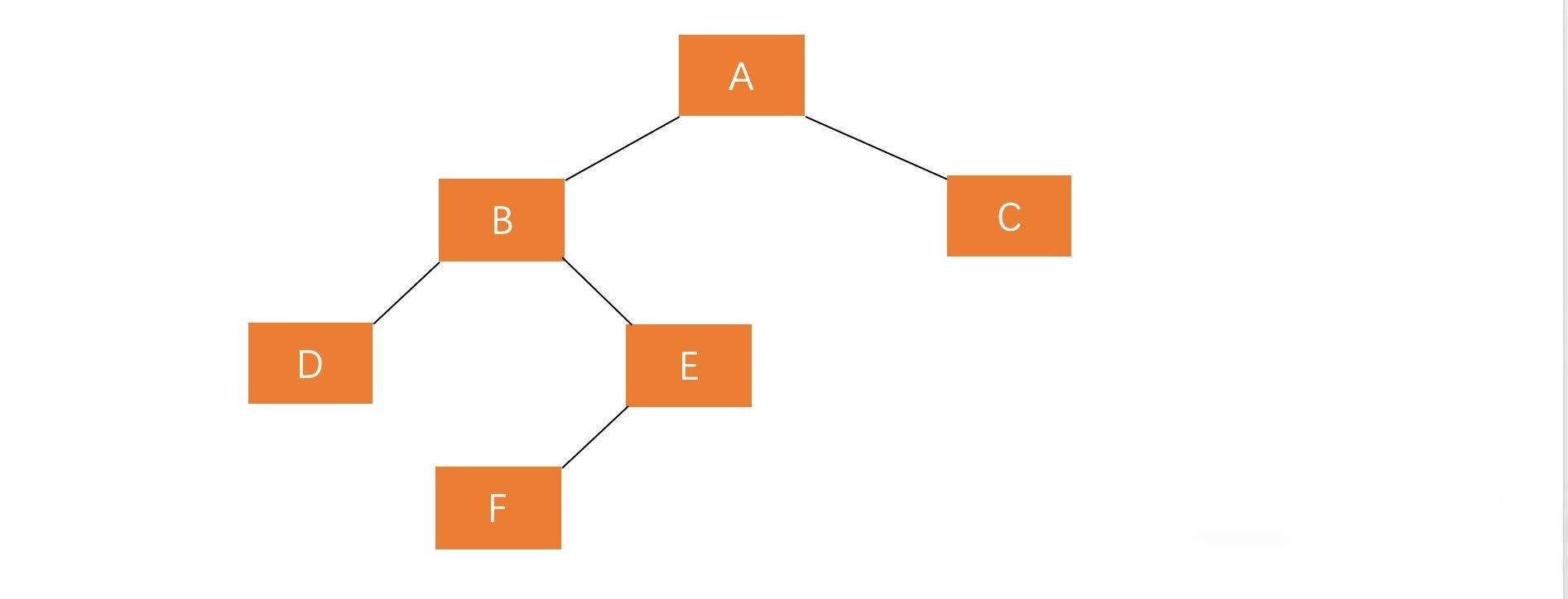
- 只右旋不能满足平衡要求
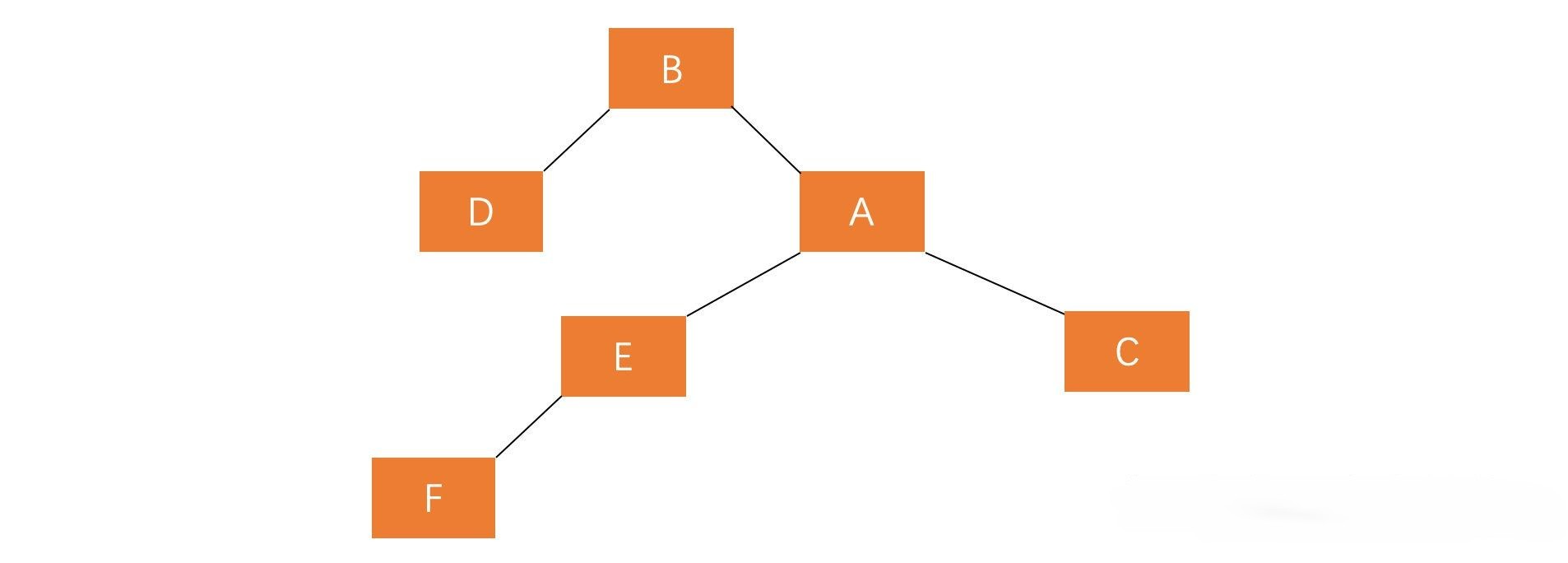
- 先对失衡节点A的左孩子进行左旋
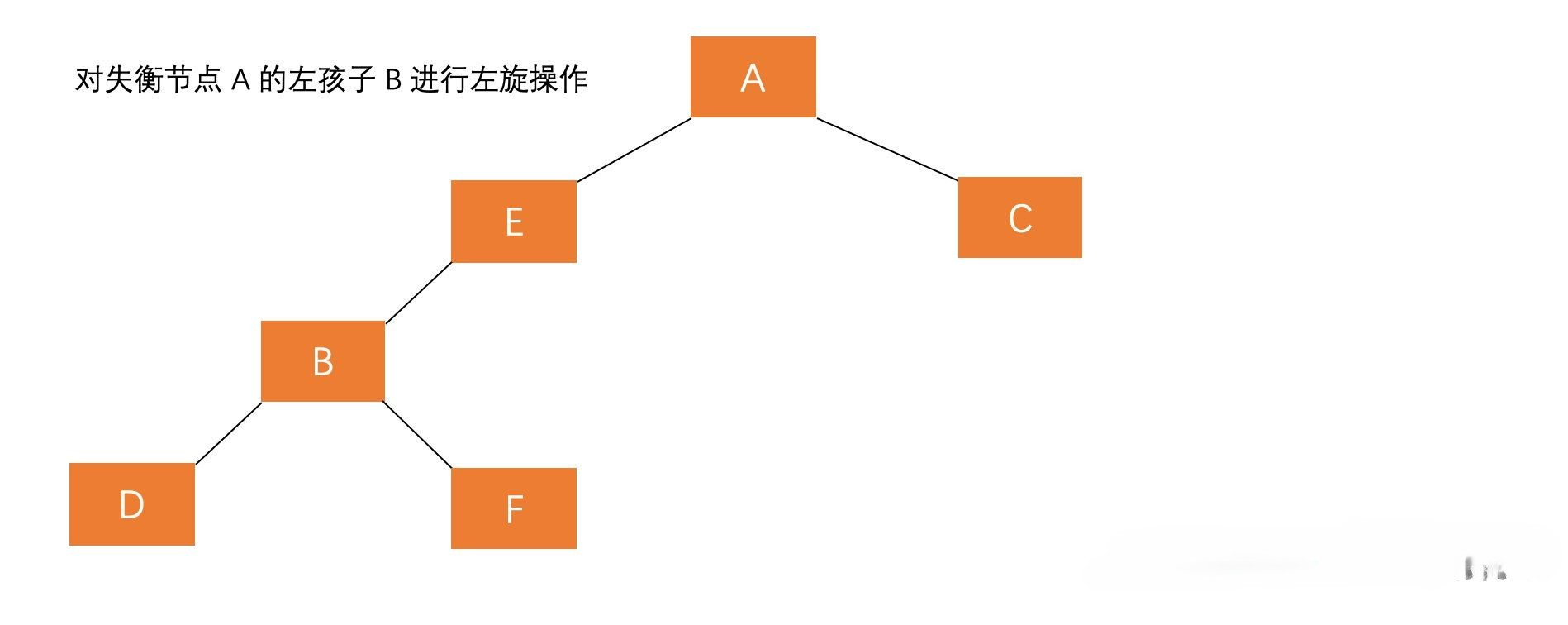
- 再对失衡节点进行右旋
RL
与LR类似,换个方向,先对失衡节点右孩子进行右旋操作,再对失衡节点进行左旋操作