https://blog.csdn.net/poisonchry/article/details/120825671?utm_medium=distribute.pc_aggpage_search_result.none-task-blog-2~aggregatepage~first_rank_ecpm_v1~rank_v31_ecpm-1-120825671.pc_agg_new_rank&utm_term=pytorch%E5%B0%86%E5%BC%A0%E9%87%8F%E8%BD%AC%E7%BD%AE&spm=1000.2123.3001.4430

    高维张量转置：

    1. >>> tensor = torch.randn(1, 2, 3)
    2. >>> tensor  # shape of tensor is [1, 2, 3]
    3. tensor([[[ 0.1264, -0.7503,  0.5522],
    4.          [ 0.0680,  1.0128,  0.1585]]])
    6. >>> tensor = torch.transpose(tensor, dim0=1, dim1=2)
    7. >>> tensor  # shape of tensor is [1, 3, 2]
    8. tensor([[[ 0.1264,  0.0680],
    9.          [-0.7503,  1.0128],
    10.          [ 0.5522,  0.1585]]])
    12. >>> tensor = torch.transpose(tensor, dim0=0, dim1=2)
    13. >>> tensor  # shape of tensor is [2, 3, 1]
    14. tensor([[[ 0.1264],
    15.          [-0.7503],
    16.          [ 0.5522]],
    18.         [[ 0.0680],
    19.          [ 1.0128],
    20.          [ 0.1585]]])

    首先，我们要先学着阅读张量表达的数据结构

    1.先看有几个括号，有几个括号就是几阶张量

    1. tensor([[[ 0.1264, -0.7503,  0.5522],
    2.          [ 0.0680,  1.0128,  0.1585]]])

    这里有三个括号，说明是三维张量。

    我们从外往里进行检索，最外层只有一个所以是1
    第二层里面有2个元素，所以是2
    第三层就到了最具体的元素层了，所以是3

    1. >>> tensor = torch.randn(1, 2, 3)
    2. >>> tensor  # shape of tensor is [1, 2, 3]
    3. tensor([[[ 0.1264, -0.7503,  0.5522],
    4.          [ 0.0680,  1.0128,  0.1585]]])

    维度主要就是看第几个括号里面有几个元素。

    这也是我们索引的主要方法

    现在我们来说，如何对高维张量进行转置

    1. >>> tensor = torch.transpose(tensor, dim0=1, dim1=2)
    2. >>> tensor  # shape of tensor is [1, 3, 2]
    3. tensor([[[ 0.1264,  0.0680],
    4.          [-0.7503,  1.0128],
    5.          [ 0.5522,  0.1585]]])
    7. >>> tensor = torch.transpose(tensor, dim0=0, dim1=2)
    8. >>> tensor  # shape of tensor is [2, 3, 1]
    9. tensor([[[ 0.1264],
    10.          [-0.7503],
    11.          [ 0.5522]],
    13.         [[ 0.0680],
    14.          [ 1.0128],
    15.          [ 0.1585]]])

    首先，原来的数据格式是 [1,3,2] 我们要转置成 [2,3,1]

    我们可以发现3是不发生改变的。

    我们换个视角看待这些数据。

    3237ac1bf93cabd692315ede0f1db1a.jpg

    由于最后一位是1，所以，我们要把三个向量组合起来

    1. >>> tensor  # shape of tensor is [2, 3, 1]
    2. tensor([[[ 0.1264],
    3.          [-0.7503],
    4.          [ 0.5522]],
    6.         [[ 0.0680],
    7.          [ 1.0128],
    8.          [ 0.1585]]])
    1. import torch
    2. import numpy as np
    3. tensor_ = torch.from_numpy(np.arange(24).reshape(1,2,3,4))
    4. print(tensor_)
    5. # tensor([[[[ 0,  1,  2,  3],
    6. #           [ 4,  5,  6,  7],
    7. #           [ 8,  9, 10, 11]],
    8. # 
    9. #          [[12, 13, 14, 15],
    10. #           [16, 17, 18, 19],
    11. #           [20, 21, 22, 23]]]])
    13. tensor_t = tensor_.transpose(1, 3)
    14. print(tensor_t)
    15. # tensor([[[[ 0, 12],
    16. #           [ 4, 16],
    17. #           [ 8, 20]],
    18. # 
    19. #          [[ 1, 13],
    20. #           [ 5, 17],
    21. #           [ 9, 21]],
    22. # 
    23. #          [[ 2, 14],
    24. #           [ 6, 18],
    25. #           [10, 22]],
    26. # 
    27. #          [[ 3, 15],
    28. #           [ 7, 19],
    29. #           [11, 23]]]])
    31. tensor_tt = tensor_t.transpose(1, 3)
    32. print(tensor_tt)
    33. # tensor([[[[ 0,  1,  2,  3],
    34. #           [ 4,  5,  6,  7],
    35. #           [ 8,  9, 10, 11]],
    36. # 
    37. #          [[12, 13, 14, 15],
    38. #           [16, 17, 18, 19],
    39. #           [20, 21, 22, 23]]]])

    本来的形状是（1，2，3，4）现在我们转变2和4，说明1和3不变

    主要关注在3这个维度。

    我们要确保3这个维度上的数据都是一组的。
    9a3a3dcab893c02d85ce7d547029551.jpg

    1. # tensor([[[[ 0, 12],
    2. #           [ 4, 16],
    3. #           [ 8, 20]],
    4. # 
    5. #          [[ 1, 13],
    6. #           [ 5, 17],
    7. #           [ 9, 21]],
    8. # 
    9. #          [[ 2, 14],
    10. #           [ 6, 18],
    11. #           [10, 22]],
    12. # 
    13. #          [[ 3, 15],
    14. #           [ 7, 19],
    15. #           [11, 23]]]])

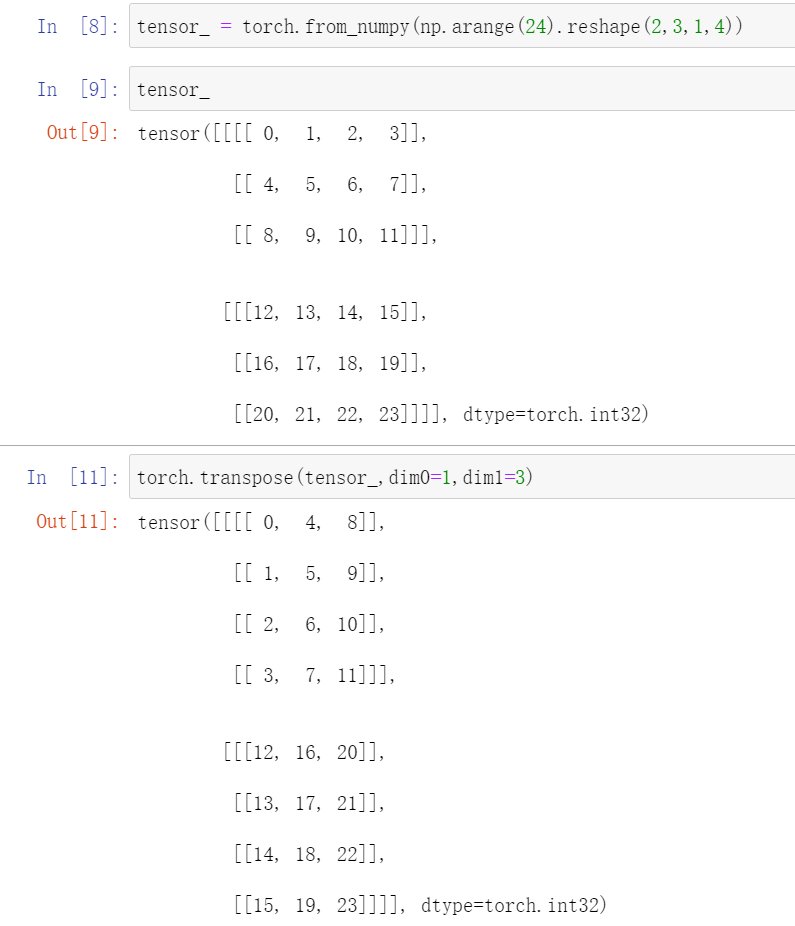
    image.png
    如果最外层是2及以上的数字，说明不同组之间的数据是不流通的。