1 惯性导航定位技术介绍

惯性是所有质量体本身的基本属性。建立在牛顿定律基础上的惯性导航系统不与外界发生任何光电联系，仅靠系统本身就能对汽车进行连续的三维定位和三维定向。
由于惯性导航系统这种能自主地、隐蔽地获取汽车完备运动信息的优势是诸如 GNSS等其他定位系统无法比拟的，所以惯性导航系统一直是自动驾驶中获取汽车位姿数据的重要手段。
惯性导航定位是一门跨多学科的技术，涉及近代数学、物理学、力学、光学、材料学、微电子和计算机等诸多领域，内容较为丰富[14]。本节将从系统简介、工作原理、误差分析等方面对惯性导航定位系统进行介绍。

2 惯性导航定位系统简介

惯性导航系统是一种不依赖于外部信息，也不向外部辐射能量的自主式导航系统[15]。 其主要由惯性测量单元、信号预处理和机械力学编排3个模块组成，如图3-7所示。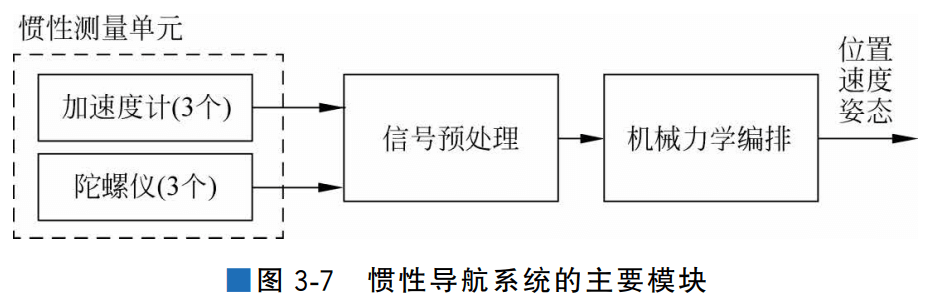
image.png
一个惯性测量单元包括3个相互正交的单轴加速度计(Accelerometer)和3个相互正交的单轴陀螺仪(Gyroscopes)。惯性测量单元结构如图3-8所示。信号预处理部分对惯性 测量单元输出信号进行信号调理、误差补偿并检查输出量范围等，以确保惯性测量单元正常 工作。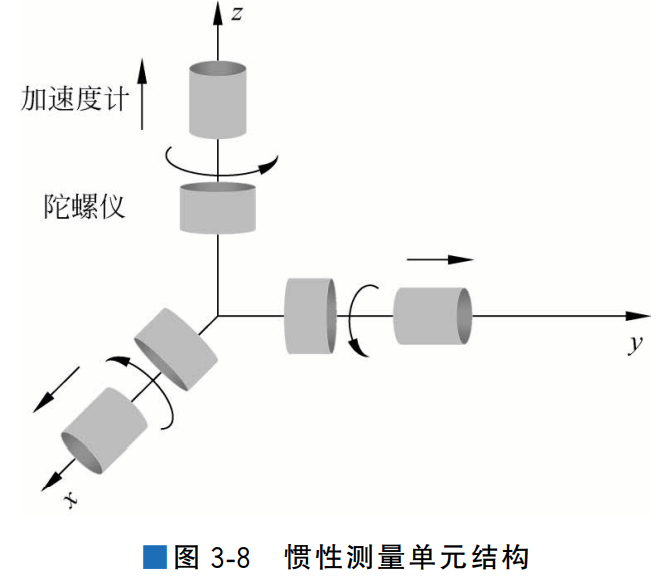
image.png
惯性导航系统根据机械力学编排形式的不同，可分为平台式惯性导航系统(Gimbaled InertialNavigationSystem，GINS)和捷联式惯性导航系统(Strap-downInertialNavigation System，SINS)，这两种系统的组成如图3-9所示。图3-9中的数学平台是为了建立导航坐 标系，计算导航数据所虚构的平台。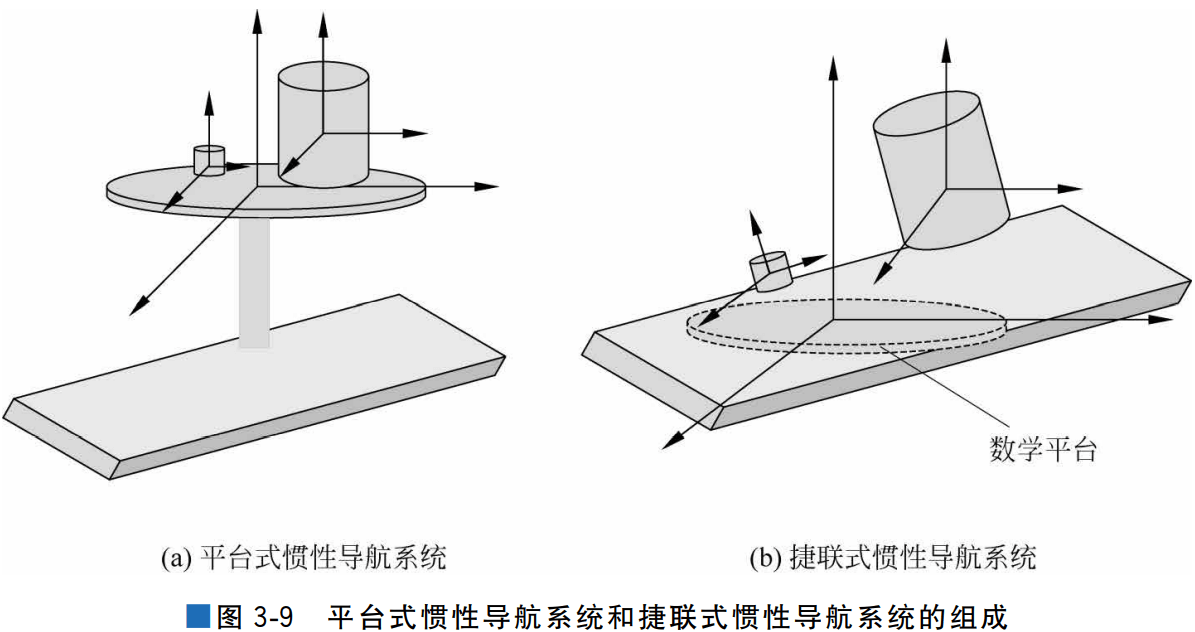
image.png
平台式惯性导航系统是将陀螺仪和加速度计等惯性测量单元通过支架平台与载体固连 的惯性导航系统。惯性测量单元固定在平台台体上，系统的敏感轴能直接模拟导航坐标系， 这就保证了敏感轴的准确指向，并且隔离了载体的角运动，给惯性测量单元提供了较好的工作环境，使得系统的精度较高，但平台台体也直接导致了系统结构复杂、体积大、制造成本高等不足。
捷联式惯性导航系统是把惯性测量单元直接固连在载体上，用计算机来完成导航平台功能的惯性导航系统，载体转动时系统的敏感轴也跟随转动，通过计算载体的姿态角就能确定出惯性测量单元敏感轴的指向，然后将惯性测量单元测量得到的载体运动信息变换 到导航坐标系上即可进行航迹递推。
基于成本控制考虑，当前自动驾驶领域常用捷联式惯性导航系统。

3 惯性导航定位系统工作原理

惯性导航系统是一种以陀螺仪和加速度计为感知元件的导航参数解算系统，应用航迹递推算法提供位置、速度和姿态等信息[16]。汽车行驶数据的采集由以陀螺仪和加速度计组成的惯性测量单元来完成。
通常说“用加速度计测量载体的运动加速度”，实际上这个说法并不确切，因为加速度计测量的不是载体的运动加速度，而是载体相对惯性空间的绝对加速度和重力加速度之和，称作“比力”。从加速度计的工作原理可知，加速度计可以输出沿敏感 轴方向的比力，其中含有载体绝对加速度。同样地，陀螺仪可以输出车体相对于惯性坐标系 的角加速度信号。以上两个惯性传感器组的敏感轴是相互平行的，共享惯性传感器组的原点和敏感轴。
因此，如果在汽车上能得到互相正交的3个敏感轴上的加速度计和陀螺仪输出，同时又已知敏感轴的准确指向，就可以掌握汽车在三维空间内的运动加速度和角速度。 惯性导航系统工作原理基于牛顿第二运动定律，其说明了加速度的大小与作用力成正比，方向与作用力的方向相同[17]，数学表达式为:
F =ma (3-1)
惯性导航系统利用载体先前的位置、惯性测量单元测量的加速度和角速度来确定其当前位置。其中，速度v 和偏移量s都可以通过对加速度a 的积分得到。
如式(3-2)、式(3-3) 所示，加速度a 经过积分得到速度v，经过二重积分得到偏移量s。相反，速度和加速度也可以通过对位移的微分而估算得到。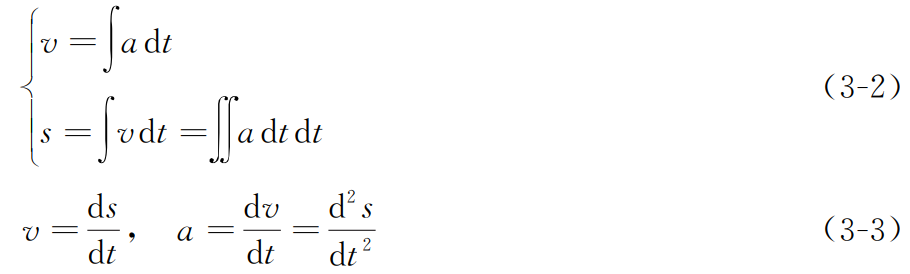
image.png
类似地，汽车的俯仰、偏航、翻滚等姿态信息都可以通过对角加速度的积分得到。利用姿态信息可以把导航参数从惯性坐标系变换到导航坐标系中[18]。
综上，惯性导航系统可以说是一个由惯性测量单元和积分器组成的积分系统。该系统通过陀螺仪测量载体旋转信息求解得到载体的姿态信息，再将加速度计测量得到的载体比力信息转换到导航坐标系进行加速度信息的积分运算，就能推算出汽车的位置和姿态信息。
从一个已知的坐标位置开始，根据载体在该点的航向、航速和航行时间，推算下一时刻该坐标位置的导航过程称为航迹递推[19]。航迹递推是一种非常原始的定位技术，最早是海上船只根据罗经和计程仪所指示的航向、航程以及船舶操纵要素与风流要素等，在不借助外界导航物标的条件下求取航迹和船位，逐渐演化成如今自动驾驶汽车定位技术中最常用的方法。
正如前面所提到的，惯性导航定位基于一个简单的原理，那就是位置的差异可以由一个加速度的双重积分得到，可以被描述为在一个稳定坐标系下并且被明确定义的与时间相关的函数，可表述为:
image.png
接下来介绍一维航迹递推和二维航迹递推的导航例子，然后，简要叙述三维航迹递推的 基本思路。

3.1 一维航迹递推

对于一维航迹递推，考虑在如图3-10所示的汽车直线(即在一个固定的方向)上移动的场景。要在这种情况下进行航迹递推，只需要将一个加速度计安装在汽车上，并使加速度计 的敏感轴方向与汽车运动方向一致，即可得到速度和位置。
已知汽车的初始位置s0、初始速度v0，通过对加速度a 进行积分即可得到汽车在t时刻的速度vt，即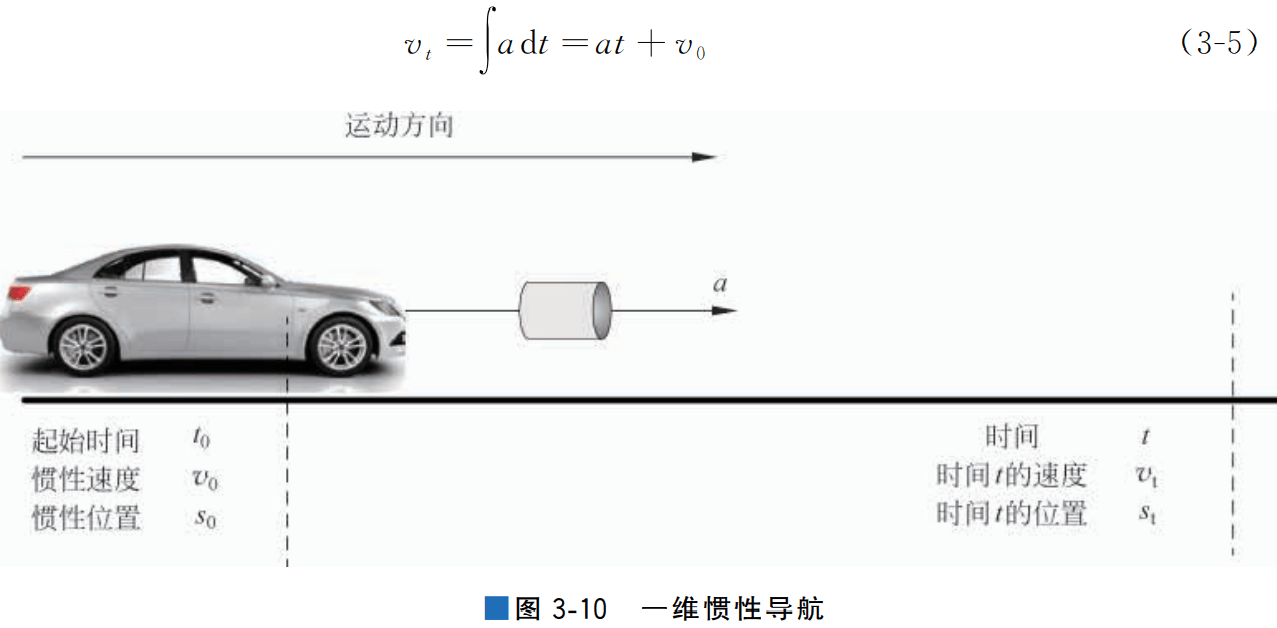
image.png
对速度vt进行积分得到汽车在t时刻的位置st：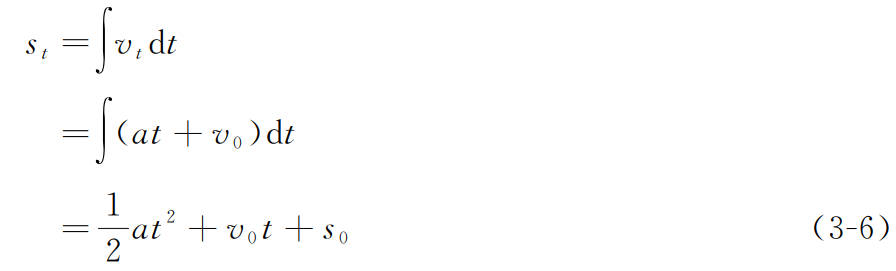
image.png

3.2 二维航迹递推

航迹递推从一维拓展到二维的难点主要在于需要将惯性坐标系(坐标轴为x、y，x 轴与 汽车航向保持一致)下的加速度变换到一个与地球固连的坐标系下，常用的是地理坐标系， 也称为导航坐标系(坐标轴为E、N，N 轴与地理北向保持一致)。
在二维航迹递推中，将汽车看作是在二维平面(x，y)上的运动，需要已知汽车的起始点 (x0，y0)和起始航向角A0。通过实时检测汽车在x、y 两个方向上的行驶距离和航向角的变化，即可实时推算汽车的二维位置。
图3-11是将曲线运动近似为直线运动的捷联 式惯性导航二维航迹递推示意图，其中黑色圆点表 示汽车位置，θ表示汽车与北向间的夹角，圆柱体表示加速度计与陀螺仪，陀螺仪敏感轴垂直于纸面向外。
在进行类似一维航迹递推中的积分运算前，需要将惯性测量单元的输出转换到导航坐标系中。 汽车转弯将使陀螺仪产生一个相对于导航坐标系 方向角变化的角速度ω，结合初始航向角 A0，对陀螺仪测量得到的角速度进行积分可以得到航向角At。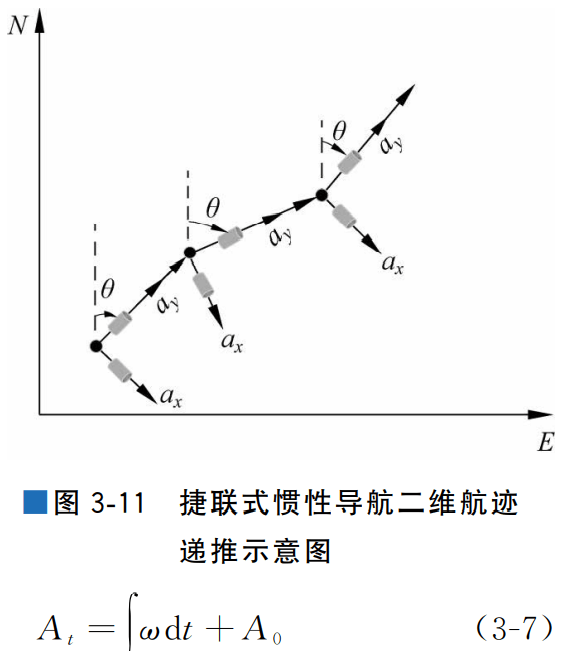
image.png
汽车速度变化将产生IMU 坐标系下的加速度ay，但是推算需要的是在导航坐标系中的加速度aN ，使用航向角At 可以将惯性测量单元的测量信息转换到导航坐标系中。坐标系的转换如图3-12所示。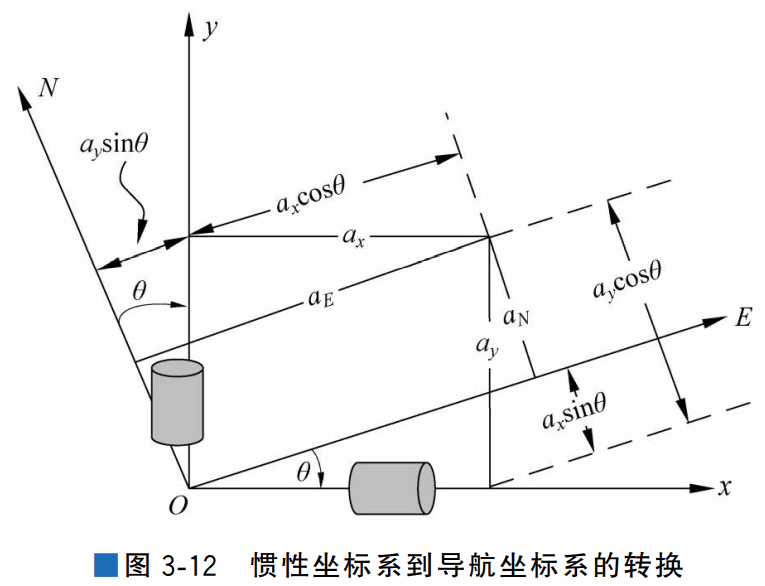
image.png
IMU 坐标轴x、y 与导航坐标轴E、N 存在夹角θ，因此加速度aE 和加速度aN 可以 写为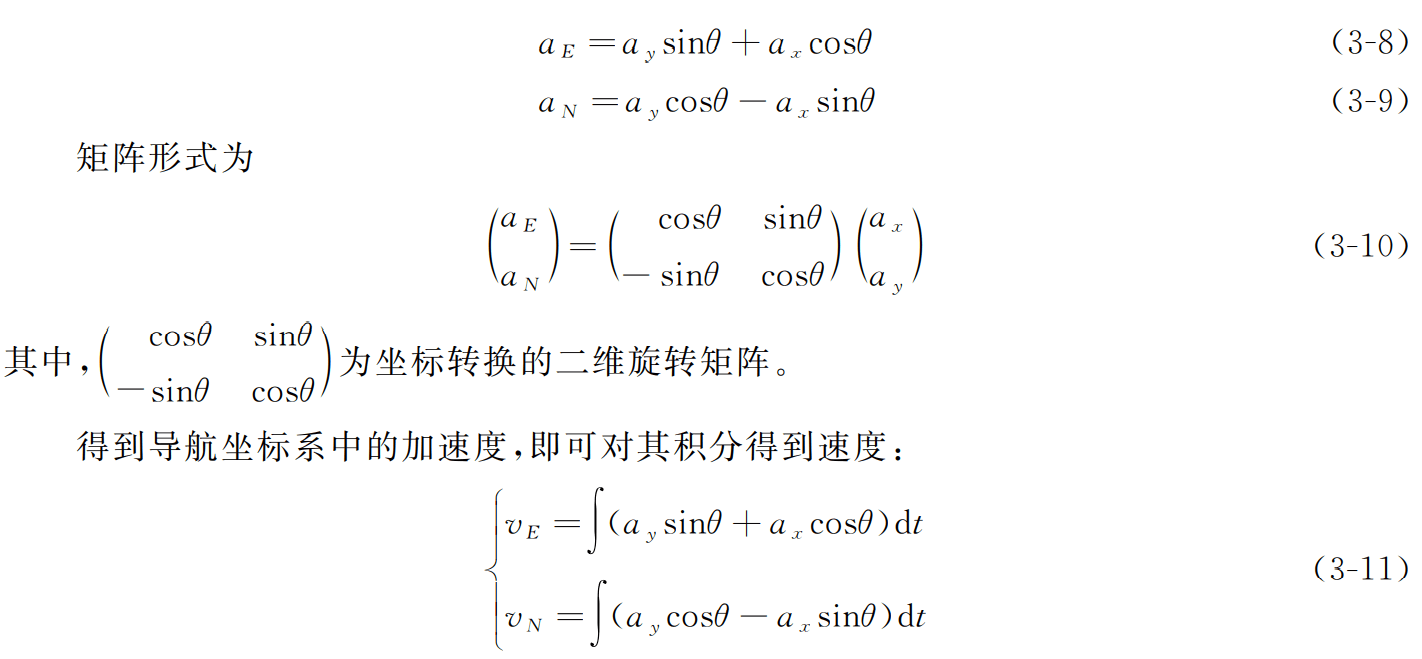
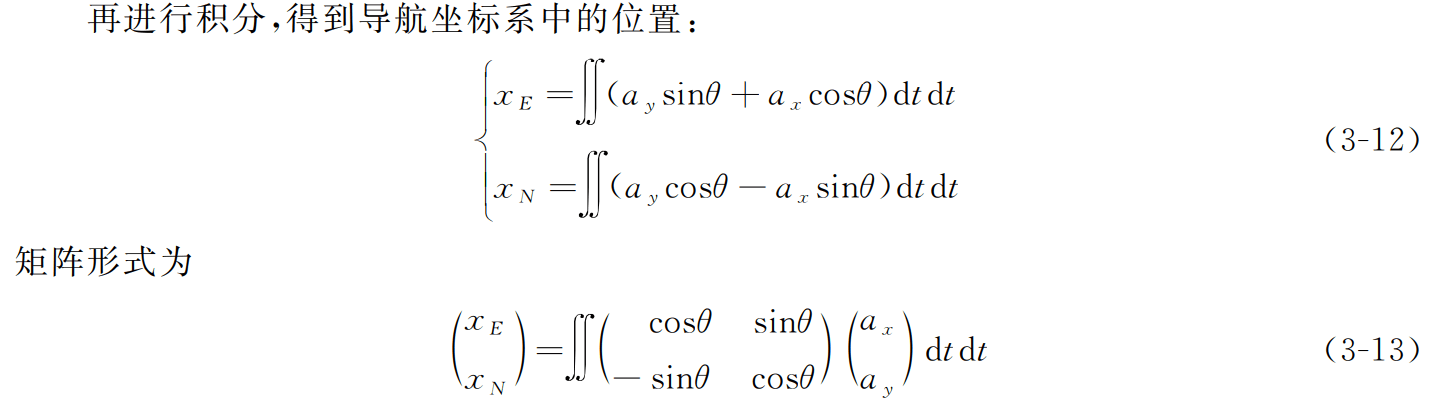
image.png
image.png

3.3 三维航迹递推

三维航迹递推需要3个陀螺仪来测量载体相对于惯性空间的旋转角速率，需要3个加速度计来测量载体相对惯性空间受到的比力。如图3-13所示，载体的合加速度是重力加速度和其他外力产生的加速度的合成。为了消除重力加速度分量，须知道加速度计相对于重力方向的角度，这个可以由解算的姿态矩阵给出。
与二维航迹递推类似，对陀螺仪测量的角速度进行积分可以得到3个姿态角，去掉重力加速度的同时通过三维旋转矩阵将加速度计 测量值投影到导航坐标系中。
下面给出基础三维旋转矩阵，其中γ、α、β角分别对应3个姿 态角翻滚角、俯仰角、航向角，式(3-14)~式(3-16)分别表示绕x、y、z 轴旋转γ、α、β角的旋 转矩阵。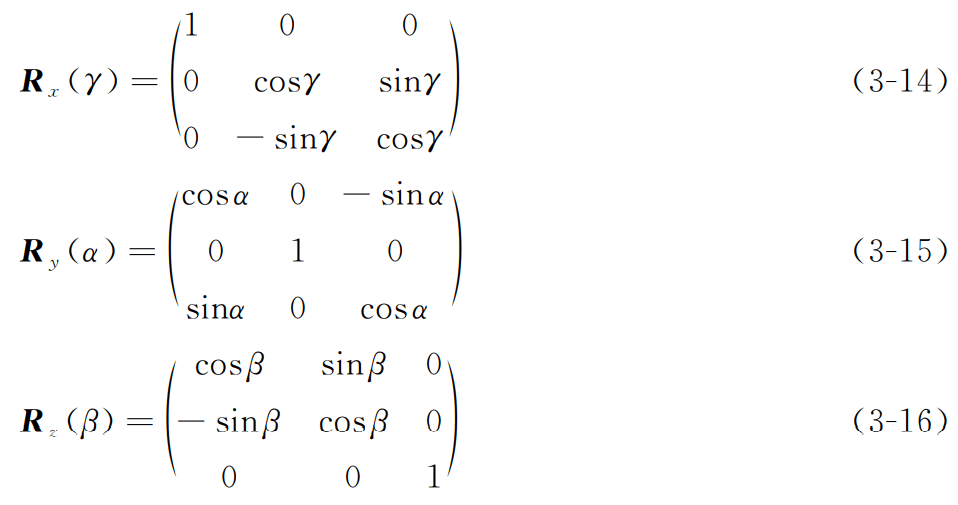
image.png
对于上述3个基础旋转矩阵，其旋转次序不可忽略，旋转次序也称顺规，顺规可以自由组合。对于γ、β、α 角在不同的顺规中有不同的复合旋转矩阵结果，例如先绕x 轴旋转γ，或 者先绕y 轴旋转β，最后会得出不同的复合旋转矩阵。
一般情况下不同顺规完成的旋转效果相同，但当y 轴旋转90°时，会导致x 轴和z 轴重合而失去x 轴的自由度，即万向节死锁 (GimbalLock)。
下面举例说明复合旋转矩阵的计算，zyx 顺规下的复合旋转矩阵为: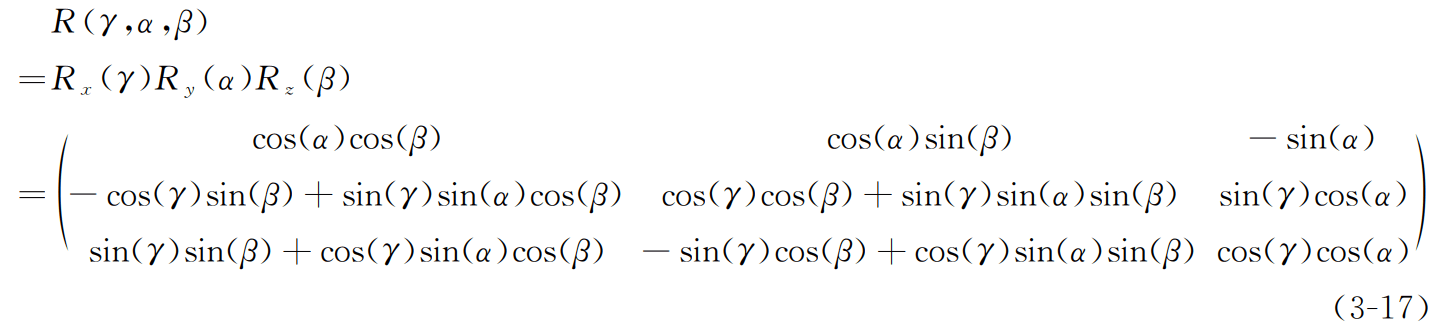
image.png
结合初始航向角，对这3个加速度做一次积分可得到三维的速度信息，通过两次积分运 算可得到三维的位置信息。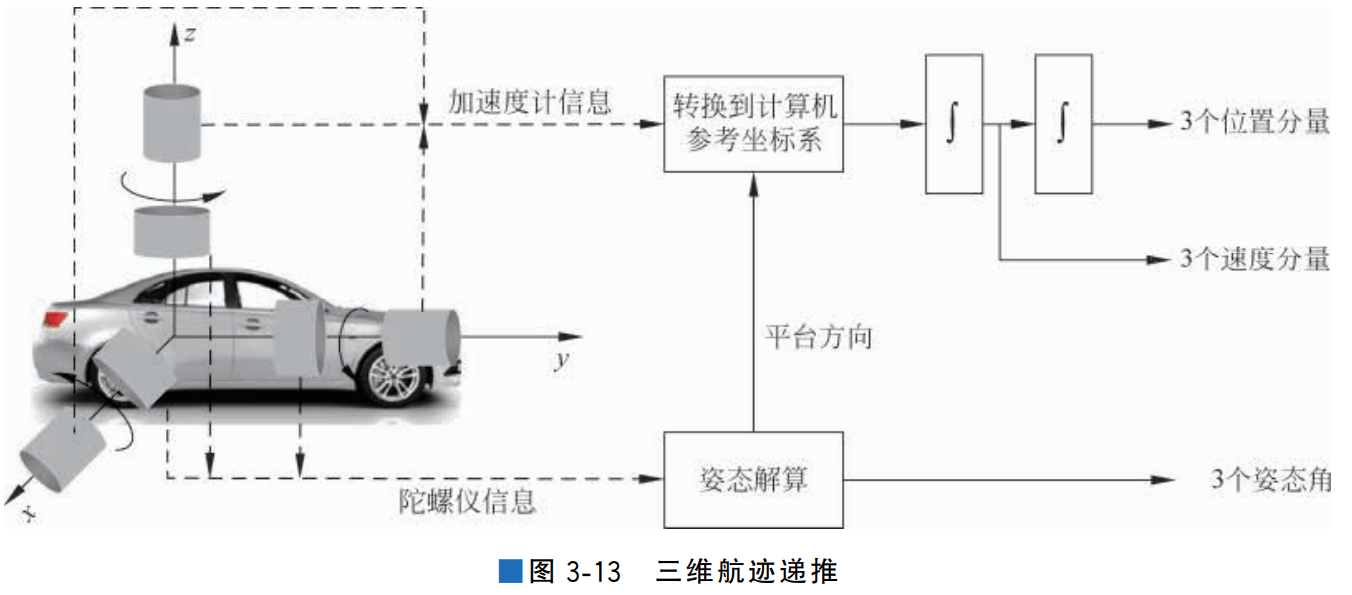
image.png

4 惯性导航定位系统误差分析

前面提到，惯性导航系统不与外界发生任何光电联系，仅靠系统本身就能对汽车进行连 续三维定位和定向，其通过在内部所感知到的情况来推断外面的情况，使得惯性导航被称为 “在盒子里导航”或“黑盒导航”。
如图3-14所示，惯性导航系统中既有电子设备，又有机械 结构，在外部冲击、振动等力学环境中，除了需要的加速度和角速度之外，还有很多误差源[20]。本节介绍随机误差和固定误差。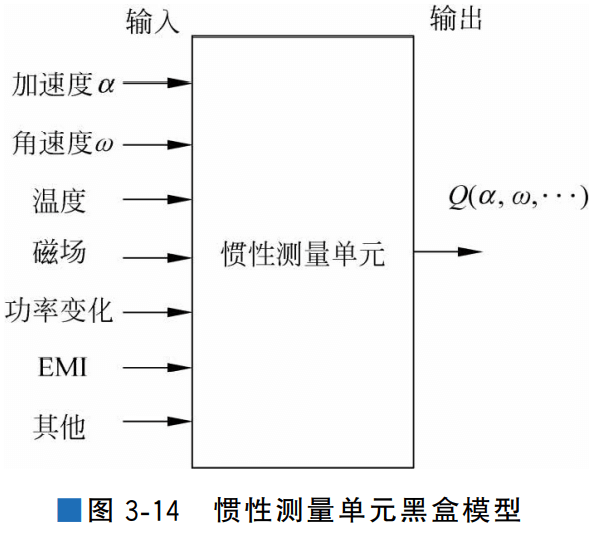
image.png

4.1 随机误差

(1)传感器白噪声误差。
该噪声通常与电子噪声合在一起，可能是来自电源、半导体设备内部的噪声或数字化过程中的量化误差。
(2)变温误差。
传感器偏差的变温误差类似时变的加性噪声源，是由外部环境温度变 化或内部热分布变化引起的。
(3)传感器随机游动误差。
在惯性测量单元中，对随机游动噪声有具体要求，但大多数都针对其输出的积分，而不是输出本身。例如，来自速率陀螺仪的“角度随机游走”等同于角速度输出白噪声的积分。
类似地，加速度计的“速度随机游走”等同于加速度计输出白噪声的积分。随机游动误差随着时间线性增大，其功率谱密度也随之下降。
(4)谐波误差。
由于热量传输延迟，所以温度控制方法(如通风与空调系统)经常引入循环误差，这些都可在传感器输出中引入谐波误差，谐波周期取决于设备的尺寸大小。同样，主载体的悬挂和结构共振也引入了谐波加速度，它会对传感器中的加速度敏感误差源产生影响。
(5)闪烁噪声误差。
闪烁噪声是陀螺仪零偏随时间漂移的主要因素。多数电子设备中都存在这种噪声，该噪声通常模型化为白噪声和随机游动的组合。

4.2 固定误差

与随机误差不同，固定误差是可重复的传感器输出误差。
常见的传感器误差模型如 图3-15所示，包括:偏差，即输入为零时传感器的任何非零的输出；尺度因子误差，常来 自标定偏差；非线性，不同程度地存在于多种传感器中；尺度因子符号不对称性，来自不匹配的推挽式的放大器；死区误差，通常由机械静摩擦力或死锁引起；量化误差，这在所有数字系统中是固有的。由于它可能存在于标准化环境中，当输入不变时它可能不是零均值的。