1. 二叉树

2. 递归序

先序遍历 : 头节点 左节点 右节点

中序遍历 : 左节点 头节点 右节点

后序遍历 : 左节点 右节点 头节点

  1.     public static class Node {
  2.         public int val;
  3.         public Node left;
  4.         public Node right;
  7.         public Node(int val) {
  8.             this.val = val;
  9.         }
  11.     }
  13.     public static void f(Node head) {
  14.         if(head == null) {
  15.             return;
  16.         }
  17.         System.out.println("先序遍历"+head.val); //头节点 左节点 右节点
  18.         f(head.left);
  19. //        System.out.println("中序遍历"+head.val); //左节点 头节点 右节点
  20.         f(head.right);
  21. //        System.out.println("后序遍历"+head.val); //左节点 右节点 头节点
  22.     }
  24.     public static void main(String[] args) {
  25.         Node head = new Node(1);
  26.         head.left = new Node(2);
  27.         head.right = new Node(3);
  28.         head.left.left = new Node(4);
  29.         head.left.right = new Node(5);
  30.         head.right.left = new Node(6);
  31.         head.right.right = new Node(8);
  33.         f(head);
  35.     }

3. 非递归版遍历二叉树顺序

使用Stack类 手动压栈出栈

3.1. 先序

  1. push头节点到栈顶 再pop弹出并输出
  2. 先push右节点 到栈中 压为栈底
  3. 再push左节点 到栈中 压为栈顶 重复上述步骤
  1. //先序遍历 头 左 右
  2. public static void pre(Node head) {
  3.     System.out.println("先序遍历");
  4.     if(head != null) {
  5.         Stack<Node> stack = new Stack<>();
  6.         stack.add(head);
  7.         while(!stack.isEmpty()) {
  8.             head = stack.pop(); //删除栈顶
  9.             System.out.println(head.value);
  10.             //先push右树 压入栈底 
  11.             if(head.right != null) {
  12.                  stack.push(head.right);
  13.             }
  14.             //再push左树 压入栈顶
  15.             if(head.left != null) {
  16.                 stack.push(head.left);
  17.             }
  18.         }
  19.     }
  20. }

3.2. 2个栈实现后序

上面我们使用1个栈实现了，先序遍历头左右的顺序，我们知道后序遍历为左右头，我们微调一下压入左右树的顺序，实现了头右左的顺序，准备第二个栈按顺序压入，再进行弹出成了左右头的顺序。

  1. //两个栈 实现后序遍历
  2. public static void pos1(Node head) {
  3.     System.out.println("后序遍历");
  4.     if(head !=null) {
  5.         Stack<Node> s1= new Stack<>();
  6.         Stack<Node> s2= new Stack<>();
  7.         s1.add(head);
  8.         while(!s1.isEmpty()) {
  9.             head = s1.pop(); 
  10.             s2.push(head);//头节点压入栈 s2栈底
  11.             if(head.left != null) {
  12.                 s1.push(head.left); //左节点 入s1栈底
  13.             }
  14.             if(head.right != null) { //右节点 入s1栈 此时为栈顶
  15.                 s1.push(head);
  16.             }
  17.             //此时s1栈存储为 [右,左]
  18.             //s2栈为 [头]  两栈结合为 [左,右,头]
  19.         }
  20.         // 左 右 头
  21.         while(!s2.isEmpty()) {
  22.             System.out.println(s2.pop().value);
  23.         }
  24.     }
  25. }

3.3. 1个栈实现后序

  1. // 一个栈 实现后序遍历
  2. public static void pos2(Node head) {
  3.     System.out.println("后序遍历2");
  4.     if (head != null) {
  5.         Stack<Node> stack = new Stack<>();
  6.         stack.push(head);
  7.         Node cur = null;
  8.         Node pre = null;
  9.         while (!stack.isEmpty()) {
  10.             cur = stack.peek(); // 只查看栈顶不删除
  11.             // 不断将左树入栈 栈顶为左树的叶子节点 pre为了防止之前入过栈的左右节点 重新入栈
  12.             if (cur.left != null && pre != cur.left && pre != cur.right) {
  13.                 stack.push(cur.left);
  14.                 // 左树无节点/已经入过栈 将右树入栈
  15.             } else if (cur.right != null && pre != cur.right) {
  16.                 stack.push(cur.right);
  17.             } else {
  18.                 // 左右都无节点 直接删除当前栈顶 为头节点
  19.                 System.out.println(stack.pop().value);
  20.                 pre = cur;
  21.             }
  22.         }
  23.     }
  24. }

3.4. 中序

  1. // 中序遍历 左 头 右
  2. public static void in(Node cur) {
  3.     System.out.println("中序遍历");
  4.     if (cur != null) {
  5.         Stack<Node> statck = new Stack<>();
  6.         while (!statck.isEmpty() || cur != null) {
  7.             if (cur != null) {
  8.                 statck.push(cur);
  9.                 cur = cur.left; // 遍历根节点 左树叶子节点 入栈
  10.             } else {
  11.                 cur = statck.pop(); // 弹出栈
  12.                 System.out.println(cur.value);
  13.                 cur = cur.right;
  14.             }
  15.         }
  16.     }
  18. }

4. 前缀树

5. 二叉树按层变遍历

即宽度优先搜索(BFS) 使用队列实现

  1. //按层遍历二叉树 bfs
  2. public static void levle(Node head) {
  3.     if(head ==null) {
  4.         return;
  5.     }
  6.     LinkedList<Node> queue = new LinkedList<>();
  7.     queue.add(head);
  8.     while(!queue.isEmpty()) {
  9.         Node cur = queue.poll();
  10.         System.out.println(cur.value);
  11.         if(cur.left != null) {
  12.             queue.add(head.left);
  13.         }
  14.         if(cur.right != null) {
  15.             queue.add(head.right);
  16.         }
  17.     }
  18. }

6. 二叉树序列化和反序列化

6.1. 先序遍历序列化

只有先序和后序遍历可以序列化，而中序遍历序列化时会有歧义（即两个节点位置不确定）

  1. // 先序 序列化二叉树
  2. public static Queue<String> preSerial(Node head) {
  3.     if (head == null) {
  4.         return null;
  5.     }
  6.     Queue<String> queue = new LinkedList<>();
  7.     pres(head, queue);
  8.     return queue;
  10. }
  12. private static void pres(Node head, Queue<String> queue) {
  13.     if (head == null) {
  14.         queue.add(null); // null节点 入栈
  15.     } else {
  16.         queue.add(String.valueOf(head.value)); // 头节点压栈
  17.         pres(head.left, queue);
  18.         pres(head.right, queue);
  19.     }
  20. }

6.2. 按层遍历序列化

  1. // 先序 反序列化二叉树
  2. public static Node buildByPreQueue(Queue<String> queue) {
  3.     if (queue == null || queue.size() == 0) {
  4.         return null;
  5.     }
  6.     return preb(queue);
  7. }
  9. private static Node preb(Queue<String> queue) {
  10.     String value = queue.poll();
  11.     if (value == null) {
  12.         return null;
  13.     }
  14.     Node head = new Node(Integer.valueOf(value));
  15.     head.left = preb(queue);
  16.     head.right = preb(queue);
  17.     return head;
  18. }

7. 431.Encode N-ary Tree to Binary Tree

设计一种算法，将 N 叉树编码为二叉树，并对二叉树进行解码，得到原始 N 叉树。N-ary 树是一个有根树，其中每个节点不超过 N 个子节点。类似地，二叉树是一个有根树，其中每个节点的子节点不超过 2 个。您的编码/解码算法的工作方式没有限制。您只需要确保可以将 N 叉树编码为二叉树，并且可以将二叉树解码为原始的 N 叉树结构。

例如，您可以通过3-ary这种方式将以下树编码为二叉树：

11. 二叉树 - 图2

请注意，以上只是一个可能会或可能不会起作用的示例。您不一定需要遵循这种格式，因此请发挥创造力并自己提出不同的方法。

思路:

将多叉树的孩子节点 全部挂载左树的右边界

  1. public static class Node {
  2.     public int val;
  3.     public List<Node> children;
  5.     public Node() {
  6.     }
  8.     public Node(int _val) {
  9.         val = _val;
  10.     }
  12.     public Node(int _val, List<Node> _children) {
  13.         val = _val;
  14.         children = _children; // 节点下所有孩子(即有多少个这个节点就有多少叉)
  15.     }
  16. };
  18. public static class TreeNode {
  19.     int val;
  20.     TreeNode left;
  21.     TreeNode right;
  23.     TreeNode(int x) {
  24.         val = x;
  25.     }
  26. }
  28. class Codec {
  29.     // 将多叉树 序列化为二叉树
  30.     public TreeNode encode(Node root) {
  31.         if (root == null) {
  32.             return null;
  33.         }
  34.         TreeNode head = new TreeNode(root.val);// 先建立 根节点
  35.         head.left = en(root.children); // 将孩子节点(多叉树)收为二叉树
  36.         return head;
  38.     }
  40.     // 孩子节点第一个全部挂载左树 剩下的孩子节点挂载在新建左树节点的右树
  41.     private TreeNode en(List<Node> children) {
  42.         TreeNode head = null;
  43.         TreeNode cur = null;
  44.         for (Node node : children) {
  45.             TreeNode tNode = new TreeNode(node.val); // 当前孩子 新生成节点
  46.             if (head == null) {
  47.                 // 当前节点为孩子节点第一个节点 应为新生成的节点
  48.                 head = tNode;
  49.             } else {
  50.                 // 否则应挂载上一个孩子节点的(head)的右树下
  51.                 head.right = tNode;
  52.             }
  53.             cur = head; // 缓存当前头
  54.             cur.left = en(node.children); // 深度优先 建立根节点左树
  55.         }
  57.         return head;
  58.     }
  60.     // 将二叉树反序列化为 多叉树
  61.     public Node decode(TreeNode root) {
  62.         if (root == null) {
  63.             return null;
  64.         }
  65.         return new Node(root.val, de(root.left));
  66.     }
  68.     private List<Node> de(TreeNode root) {
  69.         ArrayList<Node> childern = new ArrayList<>();
  70.         while (root != null) {
  71.             Node cur = new Node(root.val, de(root.left)); //先深度优先 递归到左树叶子节点
  72.             childern.add(cur); //将当前节点加入链表集合中
  73.             root = root.right;  //再while循环 将当前节点(即左树)的孩子节点 不断加入集合中
  74.         }
  75.         return childern;
  76.     }
  78. }

8. 求二叉树最大宽度

使用宽度优先搜索

  1. public static class Node {
  2.     public int value;
  3.     public Node left;
  4.     public Node right;
  6.     public Node(int v) {
  7.         value = v;
  8.     }
  9. }
  11. public static int maxWidth(Node head) {
  12.     if (head == null) {
  13.         return 0;
  14.     }
  15.     Queue<Node> queue = new LinkedList<>();
  16.     queue.add(head);
  17.     int max = 0;
  18.     int curWidth = 0; // 当前层宽度
  19.     Node curEnd = head; // 当前层尾元素
  20.     Node nextEnd = null; // 下一层尾元素
  21.     while (!queue.isEmpty()) {
  22.         Node cur = queue.poll();
  23.         curWidth++; // 增加宽度
  24.         if (cur.left != null) { // 是否有左右树
  25.             queue.add(cur.left); // 入栈
  26.             nextEnd = cur.left; // 更新下一层尾元素
  27.         }
  28.         if (cur.right != null) {
  29.             queue.add(cur.right);
  30.             nextEnd = cur.right;
  31.         }
  32.         if (cur == curEnd) {
  33.             max = Math.max(max, curWidth);
  34.             curWidth = 0; // 重置当前宽度
  35.             curEnd = nextEnd; // 更新当前尾元素 为下一层尾元素
  36.         }
  37.     }
  38.     return max;
  40. }

9. 求二叉树某个节点的后继节点

首先我们可以通过中序遍历的方式 知道某个节点的后续节点 根据中序遍历(左 头 右)的规则我们可以推断出

  1. 如果x节点有右树 后继节点为右孩子 最深的左节点

  2. 如果x节点为无右树 后继节点为离x节点最近的父辈节点并且该父辈节点以左节点形式存在

    1. 不断往上找父辈节点 并且此父辈节点是以左孩子形式存在 此时会命中 parent.rigth != nodewhile循环结束 返回此父辈节点为后继节点
    2. 不断往上找父辈节点 但父辈节点全为右孩子形式 此时会命中 parent == nullwhile循环结束 此时会返回父辈节点(此时父辈节点为null 当前节点没有后继节点)
  3. 如果x节点无右树并为左节点 后续节点为父节点

根据上述规则我们可以给每个节点添加一个parent指针(存储为父节点地址)，通过parent指针可以找到此节点的父节点

  1.     public static class Node {
  2.         public int value;
  3.         public Node left;
  4.         public Node right;
  5.         public Node parent;
  7.         public Node(int data) {
  8.             this.value = data;
  9.         }
  10.     }
  12.     public static Node getSuccessorNode(Node node) {
  13.         if (node == null) {
  14.             return null;
  15.         }
  17.         // 如果查找的节点存在右孩子 查询右树的最深的左树
  18.         if (node.right != null) {
  19.             return getLeftMost(node.right);
  20.         } else {
  21.             // 如果查找的节点不存在右孩子
  22.             Node parent = node.parent;//查询节点的父节点 
  23.             /**
  24.              * 1.如果当前查找节点为父节点的左孩子 while循环不成立 直接返回父节点即可
  25.              * 2.如果当前查找节点为父节点的右孩子 while循环成立 查找最近的父辈节点并且该父辈节点以左节点形式存在
  26.              *     2.1 不断往上找父辈节点 并且此父辈节点是以左孩子形式存在 此时会命中 `parent.rigth != node`while循环结束 返回此父辈节点为后继节点
  27.              *     2.2不断往上找父辈节点 但父辈节点全为右孩子形式 此时会命中 `parent == null`while循环结束 此时会返回父辈节点(此时父辈节点为null 当前节点没有后继节点)
  28.              */
  29.             while (parent != null && parent.right == node) {
  30.                 node = parent;
  31.                 parent = node.parent;
  32.             }
  33.             return parent;
  34.         }
  36.     }
  38.     private static Node getLeftMost(Node node) {
  39.         while (node.left != null) {
  40.             node = node.left; // 最深的 左节点
  41.         }
  42.         return node;
  43.     }

10. 折纸问题

请把一段纸条竖着放在桌子上，然后从纸条的下边向上方对折1次，压出折痕后展开
此时折痕是凹下去的，即折痕突起的方向指向纸条的背面
如果从纸条的下边向上方连续对折2次，压出折痕后展开
此时有三条折痕，从上到下依次是下折痕、下折痕和上折痕。
给定一个输入参数N，代表纸条都从下边向上方连续对折N次
请从上到下打印所有折痕的方向。
N=1时，打印: down
N=2时，打印: down down up

思路:

其实为一个比较特殊的二叉树的中序遍历，头节点为凹，左子树必定为凹，右子树必定为凸，满足以上条件中序遍历既可。

  1.     public static void printAllFolds(int N) {
  2.         process(1, N, true);
  3.         System.out.println();
  4.     }
  6.     // 当前你来了一个节点，脑海中想象的！
  7.     // 这个节点在第i层，一共有N层，N固定不变的
  8.     // 这个节点如果是凹的话，down = T
  9.     // 这个节点如果是凸的话，down = F
  10.     // 函数的功能：中序打印以你想象的节点为头的整棵树！
  11.     public static void process(int i, int N, boolean down) {
  12.         if (i > N) {
  13.             return;
  14.         }
  15.         process(i + 1, N, true);
  16.         System.out.print(down ? "凹 " : "凸 ");
  17.         process(i + 1, N, false);
  18.     }
  20.     public static void main(String[] args) {
  21.         int N = 4;
  22.         printAllFolds(N);
  23.     }

11. 判断是否为完全二叉树

一棵深度为k的有n个结点的二叉树，对树中的结点按从上至下、从左到右的顺序进行编号，如果编号为i（1≤i≤n）的结点与满二叉树中编号为i的结点在二叉树中的位置相同，则这棵二叉树称为完全二叉树。

特征:叶子结点只可能在最大的两层出，即叶子节点从左到右中间不可能出现空缺，要么出现在最后第二层和第一层。如叶子节点往下遇到null后往后的叶子节点左右节点必须为null，满足此规则即可。

如下图所示

11.1. 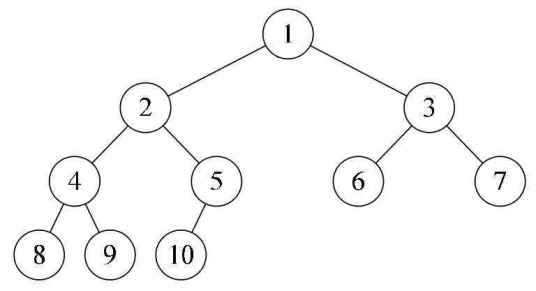11. 二叉树 - 图3

  1.     public static class Node {
  2.         public int value;
  3.         public Node left;
  4.         public Node right;
  6.         public Node(int data) {
  7.             this.value = data;
  8.         }
  9.     }
  11.     public static boolean isCBT1(Node head) {
  12.         if (head == null) {
  13.             return true;//空树 也为完全二叉树
  14.         }
  15.         LinkedList<Node> queue = new LinkedList<>();
  16.         // 是否遇到过左右两个孩子不双全的节点 标记变量
  17.         boolean leaf = false;
  18.         Node l = null;
  19.         Node r = null;
  20.         queue.add(head); //入队列
  21.         while (!queue.isEmpty()) {
  22.             head = queue.poll();
  23.             l = head.left;
  24.             r = head.right;
  25.             if (
  26.             // 如果遇到了不双全的节点之后，又发现当前节点不是叶节点
  27.                 (leaf && (l != null || r != null)) //leaf变为true 说明之前遇到了null节点
  28.                 || 
  29.                 (l == null && r != null) //左树为null 右树不为null 根节点出现空缺返回false
  31.             ) {
  32.                 return false;
  33.             }
  34.             //有左孩子 入队列
  35.             if (l != null) {
  36.                 queue.add(l);
  37.             }
  38.             //有右孩子 入队列
  39.             if (r != null) {
  40.                 queue.add(r);
  41.             }
  42.             //因为是按层遍历 到根节点了 标记变量改为true
  43.             if (l == null || r == null) {
  44.                 leaf = true;
  45.             }
  46.         }
  47.         return true;
  48.     }

12. 二叉树的递归套路

  1. 假设以X节点为头，假设可以向X左树和X右树要任何信息
  2. 在上一步的假设下，讨论以X为头节点的树，得到答案的可能性（最重要）
  3. 列出所有可能性后，确定到底需要向左树和右树要什么样的信息
  4. 把左树信息和右树信息求全集，就是任何一棵子树都需要返回的信息S
  5. 递归函数都返回S，每一棵子树都这么要求
  6. 写代码，在代码中考虑如何把左树的信息和右树信息整合出整棵树的信息

13. 求二叉树最大距离

给定一棵二叉树的头节点head，任何两个节点之间都存在距离，返回整棵二叉树的最大距离

最大距离必须为最优路径

  1. 最大距离存在左树中 不经过根节点
  2. 最大距离存在右树中 不经过根节点
  3. 最大距离不存在左右树中 必经过根节点 左树高度 + 右树高度 + 1
  1.     public static class Node {
  2.         public int value;
  3.         public Node left;
  4.         public Node right;
  6.         public Node(int data) {
  7.             this.value = data;
  8.         }
  9.     }
  11.     public static class info{
  12.         public int maxDistance; //最大距离
  13.         public int height; //高度
  14.         public info(int maxDistance, int height) {
  15.             this.maxDistance = maxDistance;
  16.             this.height = height;
  17.         }
  19.     }
  21.     public static int  maxDistance2(Node head) {
  22.         return process(head).maxDistance;
  23.     }
  25.     //深度优先
  26.     private static info process(Node head) {
  27.         if(head == null) {
  28.             return new info(0, 0); //为空null 高度为0 最大距离为0
  29.         }
  30.         info leftInfo = process(head.left);
  31.         info rightInfo = process(head.right);
  32.         int height = Math.max(leftInfo.height, rightInfo.height)+1; //高度更新
  33.         int p1 = leftInfo.maxDistance; 
  34.         int p2 = rightInfo.maxDistance;
  35.         // 如为叶子节点 则会命中此语句 携带此数 递归下去 找到最大距离
  36.         int p3 = leftInfo.height + rightInfo.height + 1; 
  37.         int maxDistance = Math.max(Math.max(p1, p2), p3); //最大距离
  38.         return new info(maxDistance,height); //返回 携带信息
  39.     }

14. 判断是否为满二叉树

判断方法一：收集整颗树的高度和节点数，只有满二叉树满足 2^h-1 = n

判断方法二：左树 和 右树为满，并且左右树高度一致，则为满二叉树

  1.     public static class Node {
  2.         public int value;
  3.         public Node left;
  4.         public Node right;
  6.         public Node(int data) {
  7.             this.value = data;
  8.         }
  9.     }
  11.     public static class info1 {
  12.         int height;
  13.         int nodes;
  15.         public info1(int height, int nodes) {
  16.             this.height = height;
  17.             this.nodes = nodes;
  18.         }
  20.     }
  22.     // 只有满二叉树满足 : 2 ^ h - 1 == n
  23.     public static boolean isFull1(Node head) {
  24.         if (head == null) {
  25.             return true;
  26.         }
  27.         info1 allInfo = process1(head);
  28.         return (1 << allInfo.height) - 1 == allInfo.nodes;
  30.     }
  32.     private static info1 process1(Node head) {
  33.         if (head == null) {
  34.             return new info1(0, 0); // 节点空返回高度0节点数0
  35.         }
  37.         info1 leftInfo = process1(head.left); // 获取左右树信息
  38.         info1 rightInfo = process1(head.right);
  39.         int height = Math.max(leftInfo.height, rightInfo.height) + 1; // 获取最大高度 +自身
  40.         int nodes = leftInfo.nodes + rightInfo.nodes + 1; // 左右节点数 +自身
  41.         return new info1(height, nodes); // 返回给上层
  42.     }
  44.     // 左树满 && 右树满 && 左右树高度一样 -> 整棵树是满的
  45.     public static boolean isFull2(Node head) {
  46.         if (head == null) {
  47.             return true;
  48.         }
  49.         return process2(head).isFull;
  51.     }
  53.     public static class info2 {
  54.         public boolean isFull;
  55.         public int height;
  57.         public info2(boolean isFull, int height) {
  58.             this.isFull = isFull;
  59.             this.height = height;
  60.         }
  62.     }
  64.     private static info2 process2(Node head) {
  65.         if (head == null) {
  66.             return new info2(true, 0);
  67.         }
  68.         info2 leftInfo = process2(head.left);
  69.         info2 rightInfo = process2(head.right);
  70.         boolean isFull = leftInfo.isFull && rightInfo.isFull && leftInfo.height == rightInfo.height;
  71.         int height = Math.max(leftInfo.height, rightInfo.height) + 1;
  73.         return new info2(isFull, height);
  75.     }

15. 求二叉树中最大的二叉搜索子树的大小

给定一棵二叉树的头节点head，返回这颗二叉树中最大的二叉搜索子树的大小

  1.     public static class Node {
  2.         public int value;
  3.         public Node left;
  4.         public Node right;
  6.         public Node(int data) {
  7.             this.value = data;
  8.         }
  9.     }
  11.     public static class info {
  12.         public int maxBSTSubtreeSize;// 最大搜索子树大小
  13.         public int allSize;// 所有子节点数量
  14.         public int max;
  15.         public int min;
  17.         public info(int maxBSTSubtreeSize, int allSize, int max, int min) {
  18.             this.maxBSTSubtreeSize = maxBSTSubtreeSize;
  19.             this.allSize = allSize;
  20.             this.max = max;
  21.             this.min = min;
  22.         }
  23.     }
  25.     public static info process(Node head) {
  26.         if (head == null) {
  27.             return null;
  28.         }
  30.         info leftInfo = process(head.left);
  31.         info rightInfo = process(head.right);
  32.         int max = head.value; // 假设为自身
  33.         int min = head.value;
  34.         int allSize = 1; // 所有字节节数 算上自身
  35.         if (leftInfo != null) {
  36.             max = Math.max(max, leftInfo.max);
  37.             min = Math.min(min, leftInfo.min);
  38.             allSize += leftInfo.allSize; // 加上左树的子节点数
  39.         }
  40.         if (rightInfo != null) {
  41.             max = Math.max(max, rightInfo.max);
  42.             min = Math.min(min, rightInfo.min);
  43.             allSize += rightInfo.allSize; //加上右树的字节点数
  44.         }
  46.         int p1 = -1;
  47.         if (leftInfo != null) {
  48.             p1 = leftInfo.maxBSTSubtreeSize;
  49.         }
  50.         int p2 = -1;
  51.         if (rightInfo != null) {
  52.             p2 = rightInfo.maxBSTSubtreeSize;
  53.         }
  54.         int p3 = -1;
  55.         //判断最大子树大小 与 所有节点数 是否相等(即没有断层)
  56.         boolean leftBst = leftInfo == null ? true : (leftInfo.maxBSTSubtreeSize == leftInfo.allSize);
  57.         boolean rightBst = rightInfo == null ? true : (rightInfo.maxBSTSubtreeSize == rightInfo.allSize);
  58.         if (leftBst && rightBst) {
  59.             // 验证当前节点是否满足二叉树规则 左孩子比自身小 右孩子比自身大
  60.             boolean leftMaxLeesX = leftInfo == null ? true : (leftInfo.max < head.value);
  61.             boolean rightMinMoreX = rightInfo == null ? true : (head.value < rightInfo.min);
  62.             if (leftMaxLeesX && rightMinMoreX) {
  63.                 //如果最大搜索子树大小没断层 并且满足搜索二叉树规则 进行递加 
  64.                 int leftSize = leftInfo == null ? 0 : leftInfo.allSize;
  65.                 int rightSize = rightInfo == null ? 0 : rightInfo.allSize;
  66.                 p3 = leftSize + rightSize + 1;
  67.             }
  68.         }
  69.         return new info(Math.max(p1, Math.max(p2, p3)), allSize, max, min);
  70.     }
  73.     public static int maxSubBSTSize2(Node head) {
  74.         if(head == null) {
  75.             return 0;
  76.         }
  77.         return process(head).maxBSTSubtreeSize;
  78.     }

16. 递归套路版判断是否为完全二叉树

上面我们使用队列按层遍历(bfs)来判断是否为完全二叉树，我们可以改为递归版本使用递归套路

17. 求二叉树最大的二叉搜索树的头节点

给定一棵二叉树的头节点head，返回这颗二叉树中最大的二叉搜索子树的头节点

18. 求二叉树上a和b两节点的最低公共祖先

给定一棵二叉树的头节点head，和另外两个节点a和b，返回a和b的最低公共祖先

  1. public static class Node {
  2.         public int value;
  3.         public Node left;
  4.         public Node right;
  6.         public Node(int data) {
  7.             this.value = data;
  8.         }
  9.     }
  11.     public static class info {
  12.         boolean findA;
  13.         boolean findB;
  14.         Node ans;
  16.         public info(boolean findA, boolean findB, Node ans) {
  17.             this.findA = findA;
  18.             this.findB = findB;
  19.             this.ans = ans;
  20.         }
  22.     }
  24.     public static Node lowestAncestor2(Node head, Node a, Node b) {
  25.         if (head == null) {
  26.             return null;
  27.         }
  28.         return process(head, a, b).ans;
  29.     }
  31.     private static info process(Node head, Node a, Node b) {
  32.         if (head == null) {
  33.             return new info(false, false, null); // 空节点 返回info信息
  34.         }
  35.         info leftInfo = process(head.left, a, b); // 递归下去
  36.         info rightInfo = process(head.right, a, b);
  37.         boolean findA = (head == a) || leftInfo.findA || rightInfo.findA; // 如果a/b为自身 或者 左右info之前发现过a/b为true
  38.         boolean findB = (head == b) || leftInfo.findB || rightInfo.findB;
  39.         Node ans = null; // 先初始化
  40.         if (findA && findB) { // a和b都标记找到
  41.             if (leftInfo.ans != null) { // 之前leftInfo有标记过祖先，继承之前的祖先，因为题目要求是最低祖先（最先找到的祖先）
  42.                 ans = leftInfo.ans;
  43.             } else if (rightInfo.ans != null) { // right同理
  44.                 ans = rightInfo.ans;
  45.             } else {
  46.                 ans = head; // 之前都没有标记过祖先 即当前节点为最先发现的祖先
  47.             }
  48.         }
  49.         return new info(findA, findB, ans); // 返回info信息
  50.     }

19. 派对的最大快乐值

公司的每个员工都符合 Employee 类的描述。整个公司的人员结构可以看作是一棵标准的、 没有环的多叉树
树的头节点是公司唯一的老板，除老板之外的每个员工都有唯一的直接上级
叶节点是没有任何下属的基层员工(subordinates列表为空)，除基层员工外每个员工都有一个或多个直接下级
这个公司现在要办party，你可以决定哪些员工来，哪些员工不来，规则：

  1. 如果某个员工来了，那么这个员工的所有直接下级都不能来

  2. 派对的整体快乐值是所有到场员工快乐值的累加

  3. 你的目标是让派对的整体快乐值尽量大

给定一棵多叉树的头节点boss，请返回派对的最大快乐值。

  1. public static class Employee {
  2.         public int happy;
  3.         public List<Employee> nexts;
  5.         public Employee(int h) {
  6.             happy = h;
  7.             nexts = new ArrayList<>();
  8.         }
  10.     }
  12.     public static class info {
  13.         int no; // 当前节点不来的情况
  14.         int yes; // 当前节点来的情况
  16.         public info(int no, int yes) {
  17.             super();
  18.             this.no = no;
  19.             this.yes = yes;
  20.         }
  22.     }
  24.     public static int maxHappy2(Employee head) {
  25.         info allInfo = process(head);
  26.         return Math.max(allInfo.no, allInfo.yes);
  27.     }
  29.     private static info process(Employee head) {
  30.         if (head == null) {
  31.             return new info(0, 0);
  32.         }
  33.         int no = 0;// 不来的情况
  34.         int yes = head.happy; // 来的情况
  35.         for (Employee employee : head.nexts) {
  36.             info nextInfo = process(employee);
  37.             no += Math.max(nextInfo.no, nextInfo.yes);// 子节点可来可不来
  38.             yes += nextInfo.no; // 当前节点来了 他的下属子节点必须得不来
  39.         }
  40.         return new info(no, yes);
  41.     }

20. 100. 相同的树

  1.     public class TreeNode {
  2.         int val;
  3.         TreeNode left;
  4.         TreeNode right;
  6.         TreeNode() {
  7.         }
  9.         TreeNode(int val) {
  10.             this.val = val;
  11.         }
  13.         TreeNode(int val, TreeNode left, TreeNode right) {
  14.             this.val = val;
  15.             this.left = left;
  16.             this.right = right;
  17.         }
  18.     }
  20.     class Solution {
  21.         public boolean isSameTree(TreeNode p, TreeNode q) {
  22.             if (p == null ^ q == null) { //有一个为空 另外一个不为空 返回
  23.                 return false;
  24.             }
  25.             if (p == null && q == null) { //两者都为空
  26.                 return true;
  27.             }
  28.             //两者值相等 && 左树相等 && 右树相等
  29.             return p.val == q.val && isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
  30.         }
  31.     }

21. 101. 对称二叉树

  1.     public class TreeNode {
  2.         int val;
  3.         TreeNode left;
  4.         TreeNode right;
  5.         TreeNode() {}
  6.         TreeNode(int val) { this.val = val; }
  7.         TreeNode(int val, TreeNode left, TreeNode right) {
  8.             this.val = val;
  9.             this.left = left;
  10.             this.right = right;
  11.         }
  12.     }
  14.     class Solution {
  15.         public boolean isSymmetric(TreeNode root) {
  16.             return isSameTree(root,root);//自己与自己比较
  17.         }
  19.         public boolean isSameTree(TreeNode p, TreeNode q) {
  20.             if (p == null ^ q == null) { //有一个为空 另外一个不为空 返回
  21.                 return false;
  22.             }
  23.             if (p == null && q == null) { //两者都为空
  24.                 return true;
  25.             }
  26.             //两者值相等 && 左树与`右树相等 && 右树与`左树相等
  27.             return p.val == q.val && isSameTree(p.left, q.right) && isSameTree(p.right, q.left);
  28.         }
  29.     }

22. 104. 二叉树的最大深度

  1.     public class TreeNode {
  2.         int val;
  3.         TreeNode left;
  4.         TreeNode right;
  6.         TreeNode() {
  7.         }
  9.         TreeNode(int val) {
  10.             this.val = val;
  11.         }
  13.         TreeNode(int val, TreeNode left, TreeNode right) {
  14.             this.val = val;
  15.             this.left = left;
  16.             this.right = right;
  17.         }
  18.     }
  20.     class Solution {
  21.         public int maxDepth(TreeNode root) {
  22.             if (root == null) {
  23.                 return 0;
  24.             }
  25.             return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
  26.         }
  27.     }

23. 105. 从前序与中序遍历序列构造二叉树

  1.     public class TreeNode {
  2.         int val;
  3.         TreeNode left;
  4.         TreeNode right;
  6.         TreeNode() {
  7.         }
  9.         TreeNode(int val) {
  10.             this.val = val;
  11.         }
  13.         TreeNode(int val, TreeNode left, TreeNode right) {
  14.             this.val = val;
  15.             this.left = left;
  16.             this.right = right;
  17.         }
  18.     }
  20.     class Solution {
  22.         public TreeNode buildTree(int[] preorder, int[] inorder) {
  23.             if (preorder == null || inorder == null || preorder.length != inorder.length) {
  24.                 return null;
  25.             }
  26.              Map<Integer, Integer> IndexMap = new HashMap<>();
  27.             for (int i = 0; i < inorder.length; i++) {
  28.                 IndexMap.put(inorder[i], i);
  29.             }
  31.             return f(preorder, 0, preorder.length - 1, inorder, 0, inorder.length - 1,IndexMap);
  32.         }
  34.         private TreeNode f(int[] preorder, int l1, int r1, int[] inorder, int l2, int r2,Map<Integer, Integer> IndexMap) {
  35.             if (l1 > r1) { //
  36.                 return null;
  37.             }
  38.             TreeNode head = new TreeNode(preorder[l1]); // 头节点
  39.             if (l1 == r1) { // 只有一个元素时
  40.                 return head;
  41.             }
  42.             int index = IndexMap.get(preorder[l1]); // 查找当前头节点在中序遍历数组的位置
  43.             // 左树构建 l1+1到 l1 + index - l2 为左树的先序遍历范围         l2到index-1为中序遍历范围
  44.             head.left = f(preorder, l1 + 1, l1 + index - l2, inorder, l2, index - 1,IndexMap); // 注意左树和右树构建采用的遍历范围均相同长度
  45.             // 右树构建 l1 + index - l2(即左树的结束范围) +1 到 r1为右树先序遍历范围         index+1到r2为右树中序遍历的范围
  46.             head.right = f(preorder, l1 + index - l2 + 1, r1, inorder, index + 1, r2,IndexMap);
  47.             return head;
  48.         }
  49.     }

24. 107. 二叉树的层序遍历 II

  1. public class TreeNode {
  2.         int val;
  3.         TreeNode left;
  4.         TreeNode right;
  6.         TreeNode() {
  7.         }
  9.         TreeNode(int val) {
  10.             this.val = val;
  11.         }
  13.         TreeNode(int val, TreeNode left, TreeNode right) {
  14.             this.val = val;
  15.             this.left = left;
  16.             this.right = right;
  17.         }
  18.     }
  20.     class Solution {
  21.         public List<List<Integer>> levelOrderBottom(TreeNode root) {
  22.             List<List<Integer>> ans = new ArrayList<>();
  23.             if (root == null) { // 根节点为空直接返回空列表
  24.                 return ans;
  25.             }
  26.             LinkedList<TreeNode> queue = new LinkedList<>();
  27.             queue.add(root); // 将头节点加入队列中
  28.             while (!queue.isEmpty()) {
  29.                 int size = queue.size(); // 获取队列当前长度
  30.                 List<Integer> tans = new LinkedList<>();
  31.                 for (int i = 0; i < size; i++) {
  32.                     TreeNode temp = queue.poll();
  33.                     tans.add(temp.val); // 获取头节点的值 放入局部队列中
  34.                     if (temp.left != null) {
  35.                         queue.add(temp.left); // 左节点非空 加入到队列中
  36.                     }
  37.                     if (temp.right != null) {
  38.                         queue.add(temp.right); // 右节点非空 加入队列中
  39.                     }
  41.                 }
  42.                 ans.add(0, tans); // 将上次队列缓存头节点清空后的节点值加入到结果集合中
  43.             }
  44.             return ans;
  46.         }
  47.     }

25. 110. 平衡二叉树

平衡二叉树:一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

  1.     public class TreeNode {
  2.         int val;
  3.         TreeNode left;
  4.         TreeNode right;
  6.         TreeNode() {
  7.         }
  9.         TreeNode(int val) {
  10.             this.val = val;
  11.         }
  13.         TreeNode(int val, TreeNode left, TreeNode right) {
  14.             this.val = val;
  15.             this.left = left;
  16.             this.right = right;
  17.         }
  18.     }
  20.     class Solution {
  21.         public boolean isBalanced(TreeNode root) {
  22.             return process(root).isBalanced; //直接返回root节点的信息
  23.         }
  25.         public class info {
  26.             public boolean isBalanced; // 是否为平衡二叉树
  27.             public int height; // 高度
  29.             public info(boolean isBalanced, int height) {
  30.                 this.isBalanced = isBalanced;
  31.                 this.height = height;
  32.             }
  34.         }
  36.         public info process(TreeNode root) {
  37.             if (root == null) { // 空节点
  38.                 return new info(true, 0);
  39.             }
  40.             info leftInfo = process(root.left); // 左树信息
  41.             info rightInfo = process(root.right); // 右树信息
  43.             int height = Math.max(leftInfo.height, rightInfo.height) + 1; // 当前节点高度为 左和右树最大值 +1
  44.             boolean isBalanced = leftInfo.isBalanced && rightInfo.isBalanced
  45.                     && Math.abs(leftInfo.height - rightInfo.height) <= 1; //左树和右树为平衡二叉树 并且 左右树高度差不大于1
  46.             return new info(isBalanced, height);
  47.         }
  49.     }

26. 98. 验证二叉搜索树

搜索二叉树:左树的值比根节点的值小，右树的值比根节点的值大

一颗搜索二叉树中序遍历是递增顺序

  1.     public class TreeNode {
  2.         int val;
  3.         TreeNode left;
  4.         TreeNode right;
  6.         TreeNode() {
  7.         }
  9.         TreeNode(int val) {
  10.             this.val = val;
  11.         }
  13.         TreeNode(int val, TreeNode left, TreeNode right) {
  14.             this.val = val;
  15.             this.left = left;
  16.             this.right = right;
  17.         }
  18.     }
  20.     class Solution {
  21.         public boolean isValidBST(TreeNode root) {
  22.             return isBST(root).isBst;
  23.         }
  25.         public class info{
  26.             boolean isBst;
  27.             int max;
  28.             int min;
  29.             public info(boolean isBst, int max, int min) {
  30.                 this.isBst = isBst;
  31.                 this.max = max;
  32.                 this.min = min;
  33.             }
  35.         }
  37.         public info isBST(TreeNode root) {
  38.             if(root == null) { //头节点为空则返回空
  39.                 return null;
  40.             }
  41.             info leftinfo = isBST(root.left); //递归进入左树
  42.             info rightinfo = isBST(root.right); //递归进入右树
  44.             int max = root.val; //假设最大值为自身
  45.             int min = root.val;//假设最小值为自身
  46.             if(leftinfo != null) { //左树非空
  47.                 max = Math.max(max, leftinfo.max); //提取左树信息
  48.                 min = Math.min(min, leftinfo.min);
  49.             }
  50.             if(rightinfo != null) {
  51.                 max = Math.max(max, rightinfo.max); //提取右树信息
  52.                 min = Math.min(min, rightinfo.min);
  53.             }
  55.             boolean bst = true; //先假设为搜索二叉树
  56.             if(leftinfo !=null && !leftinfo.isBst) { //如果左树不满足则 头节点标记为不是二叉树
  57.                 bst =false;
  58.             }
  59.             if(rightinfo !=null && !rightinfo.isBst) { //如果右树不满足则 头节点标记为不是二叉树
  60.                 bst =false;
  61.             }
  64.             boolean lefiBst = leftinfo == null ? true : (leftinfo.max < root.val); //如果左树信息为空返回ture  否则左树最大值必须小于当前节点值
  65.             boolean rightBst = rightinfo == null ? true : (rightinfo.min > root.val);//如果右树信息为空返回ture  否则右树最小值必须大于当前节点值
  66.             if(!lefiBst || !rightBst) { //不满足搜索二叉树规则
  67.                 bst = false;
  68.             }
  70.             return new info(bst, max, min);
  71.         }
  73.     }

27. 112. 路径总和

  1. public class TreeNode {
  2.         int val;
  3.         TreeNode left;
  4.         TreeNode right;
  6.         TreeNode() {
  7.         }
  9.         TreeNode(int val) {
  10.             this.val = val;
  11.         }
  13.         TreeNode(int val, TreeNode left, TreeNode right) {
  14.             this.val = val;
  15.             this.left = left;
  16.             this.right = right;
  17.         }
  18.     }
  20.     class Solution {
  22.         public boolean isSum = false;
  24.         public boolean hasPathSum(TreeNode root, int targetSum) {
  25.             if(root ==null) { //根节点为空 直接返回false
  26.                 return false;
  27.             }
  28.             tree(root, 0, targetSum);
  29.             return isSum;
  31.         }
  33.         public void tree(TreeNode root, int preSum, int sum) {
  34.             if (root.left == null && root.right == null) { //当前头节点左右子节点都为空
  35.                 if (preSum + root.val == sum) { //当前头节点值与上次sum 为target则找到
  36.                     isSum = true;
  37.                 }
  38.                 return;
  39.             }
  41.             preSum += root.val; //累加当前sum
  42.             if (root.left != null) { //左节点有叶节点 递归进去
  43.                 tree(root.left, preSum, sum);
  44.             }
  45.             if (root.right != null) { //右节点有叶节点 递归进去
  46.                 tree(root.right, preSum, sum);
  47.             }
  48.         }
  49.     }

28. 113. 路径总和 II

  1.     public class TreeNode {
  2.         int val;
  3.         TreeNode left;
  4.         TreeNode right;
  6.         TreeNode() {
  7.         }
  9.         TreeNode(int val) {
  10.             this.val = val;
  11.         }
  13.         TreeNode(int val, TreeNode left, TreeNode right) {
  14.             this.val = val;
  15.             this.left = left;
  16.             this.right = right;
  17.         }
  18.     }
  20.     class Solution {
  21.         public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
  22.             List<List<Integer>> ans = new ArrayList<>();
  23.             if (root == null) {
  24.                 return ans;
  25.             }
  26.             ArrayList<Integer> path = new ArrayList<>();
  27.             process(root, path, 0, targetSum, ans);
  28.             return ans;
  29.         }
  31.         public void process(TreeNode root, ArrayList<Integer> path, int preSum, int sum, List<List<Integer>> ans) {
  32.             if (root.left == null & root.right == null) {
  33.                 if (root.val + preSum == sum) {
  34.                     path.add(root.val); // 添加当前节点路径
  35. //                    List<Integer> newPath = copy(path); // 拷贝
  36.                     List<Integer> newPath = (List<Integer>) path.clone(); // 本质上是浅拷贝 但里面存储的是值 所以复制了里面值 如里面存储的是引用不应用深拷贝
  38.                     ans.add(newPath); // 添加到结果集合中
  39.                     path.remove(path.size() - 1); // 删除当前路径
  40.                 }
  41.             }
  42.             preSum += root.val; // 累加 无需回溯 因为是值传递 不是引用传递
  43.             path.add(root.val); // 记录节点
  44.             if (root.left != null) { // 递归
  45.                 process(root.left, path, preSum, sum, ans);
  46.             }
  47.             if (root.right != null) { // 递归
  48.                 process(root.right, path, preSum, sum, ans);
  49.             }
  50.             path.remove(path.size() - 1); // 恢复现场
  51.         }
  53.     }