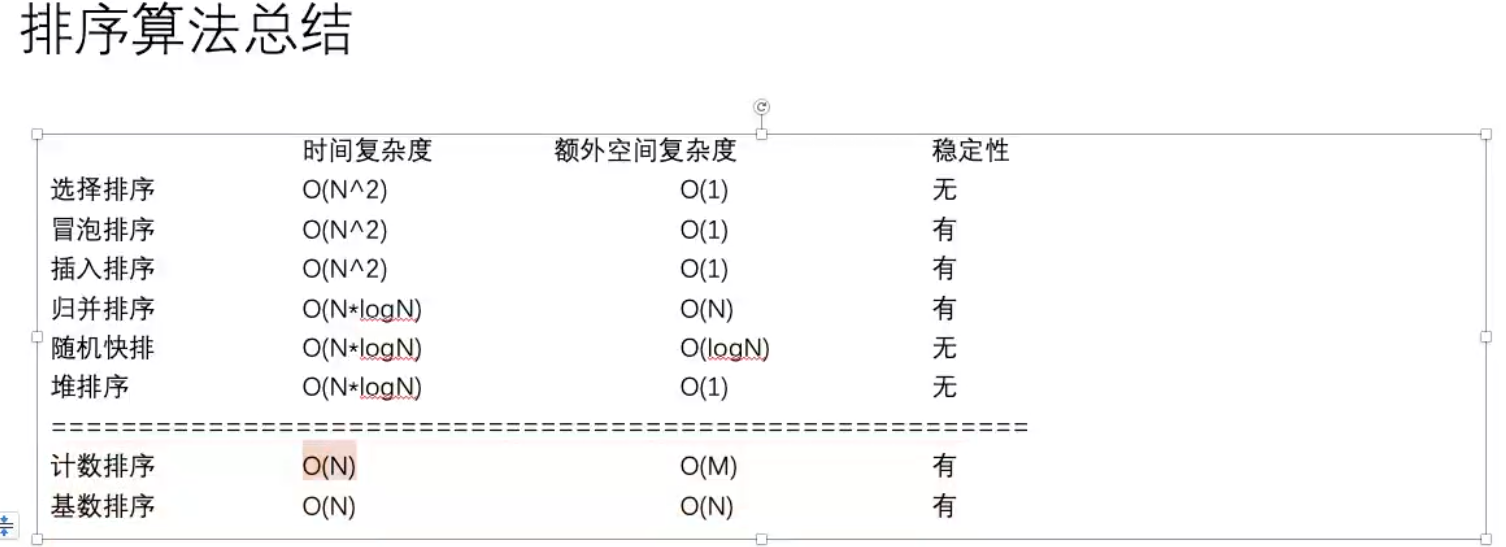
1. 排序

2. 选择排序

public static void selectionSort(int[] arr) {
        if (arr == null || arr.length < 2) {
            return;
        }
        // 0 ~ N-1  找到最小值，在哪，放到0位置上
        // 1 ~ n-1  找到最小值，在哪，放到1 位置上
        // 2 ~ n-1  找到最小值，在哪，放到2 位置上
        for (int i = 0; i < arr.length - 1; i++) {
            int minIndex = i;
            for (int j = i + 1; j < arr.length; j++) { // i ~ N-1 上找最小值的下标 
                minIndex = arr[j] < arr[minIndex] ? j : minIndex;
            }
            swap(arr, i, minIndex);
        }
    }
    public static void swap(int[] arr, int i, int j) {
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }

3. 冒泡排序

public static void bubbleSort(int[] arr) {
        if (arr == null || arr.length < 2) {
            return;
        }
        // 0 ~ N-1
        // 0 ~ N-2
        // 0 ~ N-3
        for (int e = arr.length - 1; e > 0; e--) { // 0 ~ e
            for (int i = 0; i < e; i++) {
                if (arr[i] > arr[i + 1]) {
                    swap(arr, i, i + 1);
                }
            }
        }
    }
    // 交换arr的i和j位置上的值
    public static void swap(int[] arr, int i, int j) {
        arr[i] = arr[i] ^ arr[j];
        arr[j] = arr[i] ^ arr[j];
        arr[i] = arr[i] ^ arr[j];
    }

4. 插入排序

public static void insertionSort(int[] arr) {
        if (arr == null || arr.length < 2) {
            return;
        }
        // 不只1个数
        for (int i = 1; i < arr.length; i++) { // 0 ~ i 做到有序
            for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1]; j--) {
                swap(arr, j, j + 1);
            }
        }
    }
    // i和j是一个位置的话，会出错
    public static void swap(int[] arr, int i, int j) {
        arr[i] = arr[i] ^ arr[j];
        arr[j] = arr[i] ^ arr[j];
        arr[i] = arr[i] ^ arr[j];
    }

5. 归并排序

该算法是采用分治法的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

public static void mergeSort1(int[] arr) {
        if (arr == null || arr.length < 2) { // 为空 或 小于两个元素无法排序
            return;
        }
        process(arr, 0, arr.length - 1);
    }
    public static void process(int[] arr, int l, int r) {
        if (l == r) { // 只有一个元素
            return;
        }
        int mid = l + ((r - l) / 2); // 为了防止越界 相当于(l+r)/2
        process(arr, l, mid); // 递归分治
        process(arr, mid + 1, r); // 递归
        merge(arr, l, mid, r); // 合并子序列
    }
    public static void merge(int[] arr, int l, int m, int r) {
        int[] prearr = new int[r - l + 1]; // 开辟存储排序好的数组 左右组有多少个元素就开辟多少个位置
        int index = 0; // 存储数组指针
        int p1 = l; // 左组指针
        int p2 = m + 1; // 右组指针
        while (p1 <= m && p2 <= r) { // 防止左右指针越界
            prearr[index++] = arr[p1] <= arr[p2] ? arr[p1++] : arr[p2++]; // 比较大小
        }
        while (p1 <= m) { // 左指针未越界
            prearr[index++] = arr[p1++];
        }
        while (p2 <= r) { // 右指针未越界
            prearr[index++] = arr[p2++];
        }
        // 归并到原始数组
        for (int i = 0; i < prearr.length; i++) {
            arr[l + i] = prearr[i];
        }
    }
    //非递归
    public static void mergeSort2(int[] arr) {
        if (arr == null || arr.length < 2) { // 为空或小于2个元素
            return;
        }
        int step = 1; // 步长为 1 2 4 8 16 32 2的次方(即多少个为一组)
        int N = arr.length; // 长度
        while (step < N) { // 如果步长 超过 长度
            int L = 0; // 左指针
            while (L < N) {
                int M = 0; // 右指针重置
                if (N - L >= step) { // 右指针到左指针 大于等于步长
                    M = L + step - 1; // 右指针赋值
                } else {
                    M = N - 1; // 否则右指针为 数组长度-1 为了赋值数值溢出
                }
                if (M == N - 1) { // 如果左组的 右指针为数组中最后一个则 无右组比较 直接break
                    break;
                }
                int R = 0; // 右组右指针
                if (N - 1 - M >= step) { // 右组是否能凑齐step个元素
                    R = M + step;
                } else { // 无法凑齐 右指针到数组尾元素
                    R = N - 1;
                }
                merge(arr, L, M, R); // 合并区间 L为左组左指针 M为左组右指针 M+1为右组左指针 R为右组右指针
                if (R == N - 1) { // 右组右指针到数组尾 结束本次步长
                    break;
                } else { // 否则重新赋值左组左指针 进行一个大组的区间合并
                    L = R + 1;
                }
            }
            if (step > N / 2) { // 当前步长不能凑齐左右两组 进行合并区间
                break;
            }
            step *= 2; // 步长增加
        }
    }
    // 非递归方法实现
    public static void mergeSort3(int[] arr) {
        if (arr == null || arr.length < 2) {
            return;
        }
        int N = arr.length;
        int mergeSize = 1;
        while (mergeSize < N) {
            int L = 0;
            while (L < N) {
                if (mergeSize >= N - L) { //当前步长大于剩下为合并的元素
                    break;
                }
                int M = L + mergeSize - 1; //左组右指针
                int R = M + Math.min(mergeSize, N - M - 1); //右组右指针
                merge(arr, L, M, R);
                L = R + 1;
            }
            if (mergeSize > N / 2) {
                break;
            }
            mergeSize <<= 1;
        }
    }
    // for test
    public static int[] generateRandomArray(int maxSize, int maxValue) {
        int[] arr = new int[(int) ((maxSize + 1) * Math.random())];
        for (int i = 0; i < arr.length; i++) {
            arr[i] = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
        }
        return arr;
    }
    // for test
    public static int[] copyArray(int[] arr) {
        if (arr == null) {
            return null;
        }
        int[] res = new int[arr.length];
        for (int i = 0; i < arr.length; i++) {
            res[i] = arr[i];
        }
        return res;
    }
    // for test
    public static boolean isEqual(int[] arr1, int[] arr2) {
        if ((arr1 == null && arr2 != null) || (arr1 != null && arr2 == null)) {
            return false;
        }
        if (arr1 == null && arr2 == null) {
            return true;
        }
        if (arr1.length != arr2.length) {
            return false;
        }
        for (int i = 0; i < arr1.length; i++) {
            if (arr1[i] != arr2[i]) {
                return false;
            }
        }
        return true;
    }
    // for test
    public static void printArray(int[] arr) {
        if (arr == null) {
            return;
        }
        for (int i = 0; i < arr.length; i++) {
            System.out.print(arr[i] + " ");
        }
        System.out.println();
    }
    // 对数器
    public static void main(String[] args) {
        int testTime = 500000;
        int maxSize = 100;
        int maxValue = 100;
        System.out.println("测试开始");
        for (int i = 0; i < testTime; i++) {
            int[] arr1 = generateRandomArray(maxSize, maxValue);
            int[] arr2 = copyArray(arr1);
            mergeSort1(arr1);
            mergeSort2(arr2);
            if (!isEqual(arr1, arr2)) {
                System.out.println("出错了！");
                printArray(arr1);
                printArray(arr2);
                break;
            }
        }
        System.out.println("测试结束");
    }

5.1. 求数组小和

给一个数组arr[L-R]范围既要排好序,也要返回每个元素在排序前比当前元素小的和

public static int smallSum(int[] arr) {
        if (arr == null || arr.length < 2) {
            return 0;
        }
        return process(arr, 0, arr.length - 1);
    }
    private static int process(int[] arr, int l, int r) {
        if (l == r) {
            return 0;
        }
        int mid = l + ((r - l) >> 1);
        return process(arr, l, mid) + process(arr, mid + 1, r) + merge(arr, l, mid, r);
    }
    private static int merge(int[] arr, int l, int mid, int r) {
        int[] arr2 = new int[r - l + 1];
        int i = 0;
        int p1 = l;
        int p2 = mid + 1;
        int ans = 0; // 当前归并最小和
        while (p1 <= mid && p2 <= r) {
            ans += arr[p1] < arr[p2] ? arr[p1] * (r - p2 + 1) : 0; // 如果先放入左组 则代表有r-p2+1个元素大于当前左组的元素 否则没有最小
            arr2[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++]; // 比较大小归并 如等于先放右组避免将相同值元素统计到r-p2+1中
        }
        while (p1 <= mid) {
            arr2[i++] = arr[p1++];
        }
        while (p2 <= r) {
            arr2[i++] = arr[p2++];
        }
        for (i = 0; i < arr2.length; i++) {
            arr[l + i] = arr2[i];
        }
        return ans;
    }
    // for test
    public static int comparator(int[] arr) {
        if (arr == null || arr.length < 2) {
            return 0;
        }
        int res = 0;
        for (int i = 1; i < arr.length; i++) {
            for (int j = 0; j < i; j++) {
                res += arr[j] < arr[i] ? arr[j] : 0;
            }
        }
        return res;
    }

5.2. 求数组中的逆序对数量

给定一个数组arr，求数组的降序对总数量

在一个数组中，任何一个前面的数a，和任何一个后面的数b，如果(a,b)是降序的，就称为降序对

public static int reverPairNumber(int[] arr) {
        if (arr == null || arr.length == 0) {
            return 0;
        }
        return prcess(arr, 0, arr.length - 1);
    }
    public static int prcess(int[] arr, int l, int r) {
        if (l == r) {
            return 0;
        }
        int m = l + ((r - l) >> 1);
        return prcess(arr, l, m) + prcess(arr, m + 1, r) + merge(arr, l, m, r);
    }
    public static int merge(int[] arr, int l, int m, int r) {
        int ans = 0;
        int[] help = new int[r - l + 1];
        // 倒着遍历
        int i = help.length - 1; // 从尾部开始
        int p1 = m; // 左边边界
        int p2 = r; // 右组边界
        while (p1 >= l && p2 > m) {
            ans += arr[p1] > arr[p2] ? (p2 - m) : 0; // 如果左边指针数大于右边指针数则为降序对
            help[i--] = arr[p1] > arr[p2] ? arr[p1--] : arr[p2--];
        }
        while (p1 >= l) {
            help[i--] = arr[p1--];
        }
        while (p2 > m) { // 注意到m就停止
            help[i--] = arr[p2--];
        }
        for (int j = 0; j < help.length; j++) {
            arr[l + j] = help[j];
        }
        return ans;
    }

5.3. 493. 翻转对

在一个数组中，对于任何一个数num，求有多少个(后面的数*2)依然<num，返回总个数

比如：[3,1,7,0,2]
3的后面有：1，0
1的后面有：0
7的后面有：0，2
0的后面没有
2的后面没有
所以总共有5个

5.4. 327. 区间和的个数

public int countRangeSum(int[] nums, int lower, int upper) {
        if (nums == null || nums.length == 0) {
            return 0;
        }
        // 前缀和数组
        long[] sum = new long[nums.length];
        sum[0] = nums[0];
        for (int i = 1; i < nums.length; i++) {
            sum[i] = sum[i - 1] + nums[i];
        }
        // 原数组 已无用 传递前缀和数组
        return process(sum, 0, nums.length - 1, lower, upper);
    }
    private int process(long[] sum, int l, int r, int lower, int upper) {
        if (l == r) {
            // 只有一个数时 判断是否在lower和upper范围内 是则res+1
            return sum[l] >= lower && sum[l] <= upper ? 1 : 0;
        }
        int m = l + ((r - l) >> 1);
        // 递归+合并
        return process(sum, l, m, lower, upper) + process(sum, m + 1, r, lower, upper)
                + merge(sum, l, m, r, lower, upper);
    }
    private int merge(long[] sum, int l, int m, int r, int lower, int upper) {
        int ans = 0;
        int windowL = l;
        int windowR = l; // [windowL, windowR)
        for (int i = m + 1; i <= r; i++) { // 从右组开始遍历
            long min = sum[i] - upper;
            long max = sum[i] - lower;
            while (windowR <= m && sum[windowR] <= max) {
                windowR++; // 找到最大值下标边界
            }
            while (windowL <= m && sum[windowL] < min) {
                windowL++; // 最小值下标边界
            }
            ans += windowR - windowL; // 右组当前元素有多少个在范围内的
        }
        //归并
        long[] help = new long[r - l + 1];
        int i = 0;
        int p1 = l;
        int p2 = m + 1;
        while (p1 <= m && p2 <= r) {
            help[i++] = sum[p1] <= sum[p2] ? sum[p1++] : sum[p2++];
        }
        while (p1 <= m) {
            help[i++] = sum[p1++];
        }
        while (p2 <= r) {
            help[i++] = sum[p2++];
        }
        for (int j = 0; j < help.length; j++) {
            sum[l + j] = help[j];
        }
        return ans;
    }

6. 快速排序

    // 递归经典写法
    public static void QuickSort(int[] arr, int l, int r) {
        if (l >= r) {
            return;
        }
        int left = l;
        int right = r;
        int base = arr[r]; // 以最后一个为基准 如果以头为基准则应该先找大于基准 再找小于基准的
        while (left < right) {
            // 将小于等于base的放到左边 则应该left++
            while (arr[left] <= base && left < right) {
                left++;
            }
            // 将大于等于base的放到右边 则right--
            while (arr[right] >= base && left < right) {
                right--;
            }
            if (left < right) {
                // 交换
                int temp = arr[left];
                arr[left] = arr[right];
                arr[right] = temp;
            }
        }
        arr[r] = arr[left]; // 将小于基准的最后一个数 交换到base位置
        arr[left] = base; // 将base值 交换到小于基准的位置
        // 拆分大问题 递归
        QuickSort(arr, l, left - 1);
        QuickSort(arr, right + 1, r);
    }
    public static void swap(int[] arr, int i, int j) {
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }

6.1. 荷兰国旗问题

荷兰国旗是由红白蓝3种颜色的条纹拼接而成，把这些条纹按照颜色排好，红色的在上半部分，白色的在中间部分，蓝色的在下半部分，我们把这类问题称作荷兰国旗问题。

其核心思想为 分区 小于基准放左边 等于基准的放中间 大于基准的放右边

    public static void swap(int[] arr, int i, int j) {
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }
    // arr[L...R] 玩荷兰国旗问题的划分，以arr[R]做划分值
    // <arr[R]    ==arr[R]    > arr[R]
    public static int[] netherlandsFlag(int[] arr, int L, int R) {
        if (L > R) { // L...R L>R
            return new int[] { -1, -1 };
        }
        if (L == R) {
            return new int[] { L, R };
        }
        int less = L - 1; // < 区 右边界
        int more = R; // > 区 左边界
        int index = L;
        while (index < more) { // 当前位置，不能和 >区的左边界撞上
            if (arr[index] == arr[R]) {
                index++;
            } else if (arr[index] < arr[R]) {
//                swap(arr, less + 1, index);
//                less++;
//                index++;                        
                swap(arr, index++, ++less);
            } else { // >
                swap(arr, index, --more);
            }
        }
        swap(arr, more, R); // <[R]   =[R]   >[R]
        return new int[] { less + 1, more }; //返回的是等于区的开始节点与结束节点
    }

6.2. 快排1.0

1.0效率低下 每次是最差情况 只将基准放置在排序后的位置 O(N^2)

    public static void swap(int[] arr, int i, int j) {
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }
    // arr[L..R]上，以arr[R]位置的数做划分值
    // <= X > X
    // <= X X
    public static int partition(int[] arr, int L, int R) {
        if (L > R) {
            return -1;
        }
        if (L == R) {
            return L;
        }
        int lessEqual = L - 1;
        int index = L;
        while (index < R) {
            if (arr[index] <= arr[R]) { //此为小于等于基准
                swap(arr, index, ++lessEqual);
            }
            index++;
        }
        swap(arr, ++lessEqual, R);
        return lessEqual; //返回小于等于区的边界下标(即大小-1)
    }
        public static void process1(int[] arr, int L, int R) {
        if (L >= R) {
            return;
        }
        // L..R partition arr[R] [ <=arr[R] arr[R] >arr[R] ]
        //只有两个区 小于等于区 和 大于区
        //1.0效率低下 每次是最差情况 只将基准放置在排序后的位置  O(N^2)
        int M = partition(arr, L, R);
        process1(arr, L, M - 1);
        process1(arr, M + 1, R);
    }
        public static void quickSort1(int[] arr) {
        if (arr == null || arr.length < 2) {
            return;
        }
        process1(arr, 0, arr.length - 1);
    }

6.3. 快排2.0

2.0优化每次排序 等于区的数，但最差情况仍有可能每次选中的基准只有1个（不重复）

    public static void swap(int[] arr, int i, int j) {
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }
        // arr[L...R] 玩荷兰国旗问题的划分，以arr[R]做划分值
    // <arr[R]    ==arr[R]    > arr[R]
    public static int[] netherlandsFlag(int[] arr, int L, int R) {
        if (L > R) { // L...R L>R
            return new int[] { -1, -1 };
        }
        if (L == R) {
            return new int[] { L, R };
        }
        int less = L - 1; // < 区 右边界
        int more = R; // > 区 左边界
        int index = L;
        while (index < more) { // 当前位置，不能和 >区的左边界撞上
            if (arr[index] == arr[R]) {
                index++;
            } else if (arr[index] < arr[R]) {
//                swap(arr, less + 1, index);
//                less++;
//                index++;                        
                swap(arr, index++, ++less);
            } else { // >
                swap(arr, index, --more);
            }
        }
        swap(arr, more, R); // <[R]   =[R]   >[R]
        return new int[] { less + 1, more }; //返回的是等于区的开始节点与结束节点
    }
        // arr[L...R] 排有序，快排2.0方式
    public static void process2(int[] arr, int L, int R) {
        if (L >= R) {
            return;
        }
        // [ equalArea[0]  ,  equalArea[0]]
        int[] equalArea = netherlandsFlag(arr, L, R);
        process2(arr, L, equalArea[0] - 1);
        process2(arr, equalArea[1] + 1, R);
    }
        public static void quickSort2(int[] arr) {
        if (arr == null || arr.length < 2) {
            return;
        }
        process2(arr, 0, arr.length - 1);
    }

6.4. 随机快排3.0

由于我们选择基准是最右的数，有可能会出现最差情况，即每次以右为基准时等于区只有它自身，我们可以在进行分区操作时 在l到r范围内 随机抽取一个数与r位置(基准位置)作交换，避免了每次命中最差情况。

    public static void swap(int[] arr, int i, int j) {
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }
        // arr[L...R] 玩荷兰国旗问题的划分，以arr[R]做划分值
    // <arr[R]    ==arr[R]    > arr[R]
    public static int[] netherlandsFlag(int[] arr, int L, int R) {
        if (L > R) { // L...R L>R
            return new int[] { -1, -1 };
        }
        if (L == R) {
            return new int[] { L, R };
        }
        int less = L - 1; // < 区 右边界
        int more = R; // > 区 左边界
        int index = L;
        while (index < more) { // 当前位置，不能和 >区的左边界撞上
            if (arr[index] == arr[R]) {
                index++;
            } else if (arr[index] < arr[R]) {
//                swap(arr, less + 1, index);
//                less++;
//                index++;                        
                swap(arr, index++, ++less);
            } else { // >
                swap(arr, index, --more);
            }
        }
        swap(arr, more, R); // <[R]   =[R]   >[R]
        return new int[] { less + 1, more }; //返回的是等于区的开始节点与结束节点
    }
        public static void process3(int[] arr, int L, int R) {
        if (L >= R) {
            return;
        }
        swap(arr, L + (int) (Math.random() * (R - L + 1)), R);//在l到r范围内随机选一个数 交换到r位置,避免多次命中最差情况
        int[] equalArea = netherlandsFlag(arr, L, R);
        process3(arr, L, equalArea[0] - 1);
        process3(arr, equalArea[1] + 1, R);
    }
    public static void quickSort3(int[] arr) {
        if (arr == null || arr.length < 2) {
            return;
        }
        process3(arr, 0, arr.length - 1);
    }

7. 排序稳定性

稳定性指是同样大小的样本 再次进行排序之后不会改变相对次序

对于基础类型来说 稳定性没有意义

对于非基础类型来说 稳定性有重要的意义

有的排序算法可以实现成稳定的 而有的排序算法无论如何都实现不成稳定