1. 树

2. 二叉树

每个个节点存放4个属性分别为 父节点地址 值 左子节点地址 右子节点地址

度: 每个节点的子节点数量 左右子节点的总数

在二叉树中,任意一个节点的度要小于等于2

查找效率慢

3. 二叉查找树

二叉查找树,又称二叉排序树或二叉搜索树

特点:

1. 每个节点最多有两个子节点
2. 每个节点的左子结点都是小于自身的
3. 每个节点的右子结点都是大于自身的

查找效率比普通二叉树快

3.1. 添加节点

规则:

1. 小的存左边
2. 大的存右边
3. 一样的不存

首先与根节点做比较,再逐层比较

查询效率比二叉查找树快

4. 平衡二叉树

• 二叉树左右两个子树的高度差不超过1
• 任意节点的左右两个字树都是一颗平衡二叉树

4.1. 左旋

当添加一个节点破坏了平衡二叉树规则时,并且是添加在根节点右边,我们可以通过左旋来恢复平衡二叉树.

只需要把根节点向左下方拉扯,并且连接的所有节点跟着移动即可.

当添加12节点时破坏了平衡二叉树了

我们通过左旋来恢复平衡,把根节点的右子节点往上拉

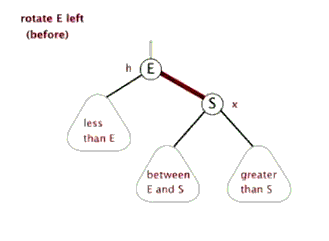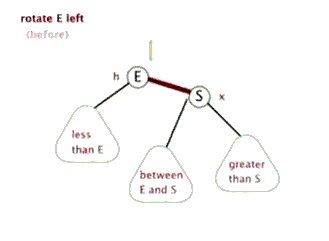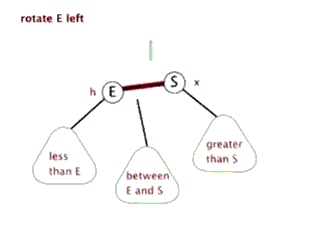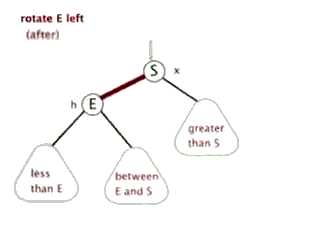
4.1.1. 如果被提级的节点已有左节点

先忽略左子节点存在,再提级,然后放置在原先的根节点的右子节点

左旋:就是将根节点的右侧往左拉,原先的右子节点变成新的父节点,并把多余的左子节点出让,给已经降级的根节点当右子节点

4.2. 右旋

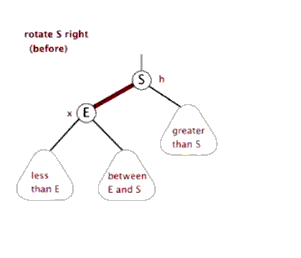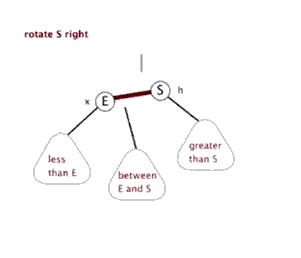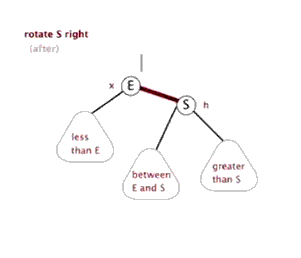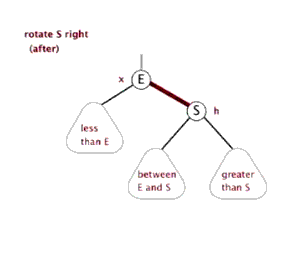
右旋:将根节点的左侧往右拉,左子节点变成了新的父节点,并把多余的右子节点出让,给已经降级根节点当左子节点

4.2.1. 左左

当根节点左子树的左子树有节点插入,导致二叉树不平衡

我们只需要将此二叉树右旋既可

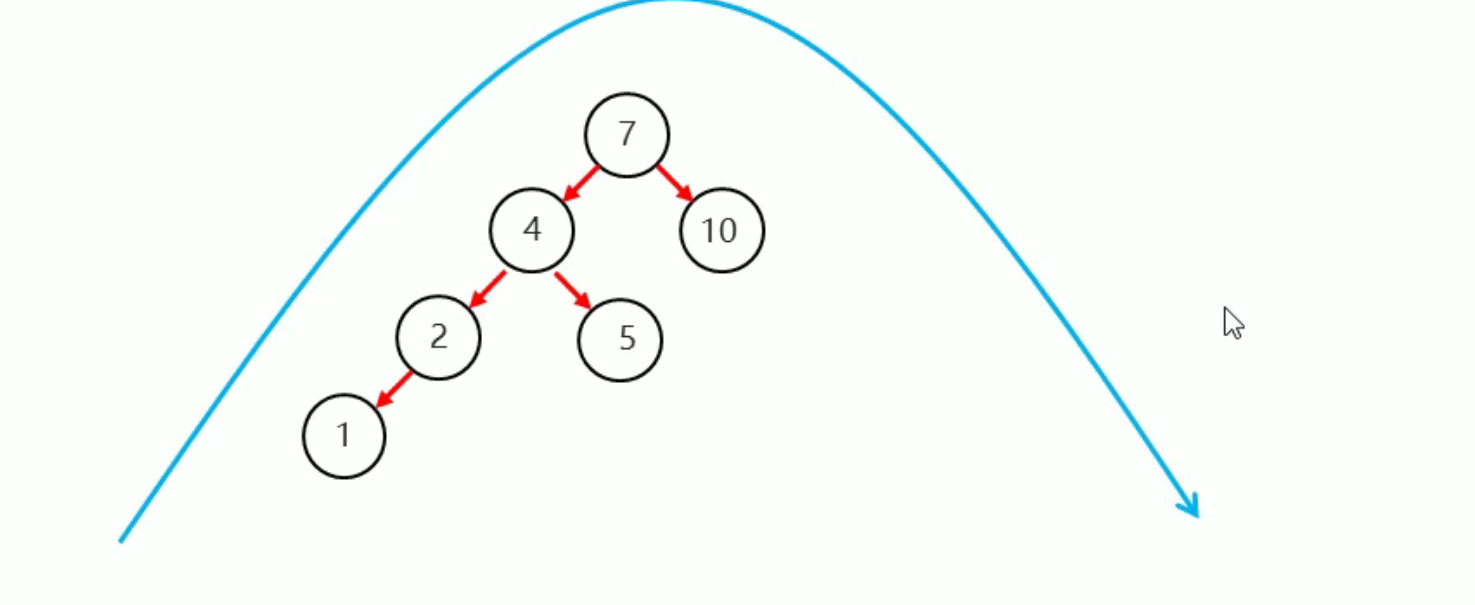
4.2.2. 右右

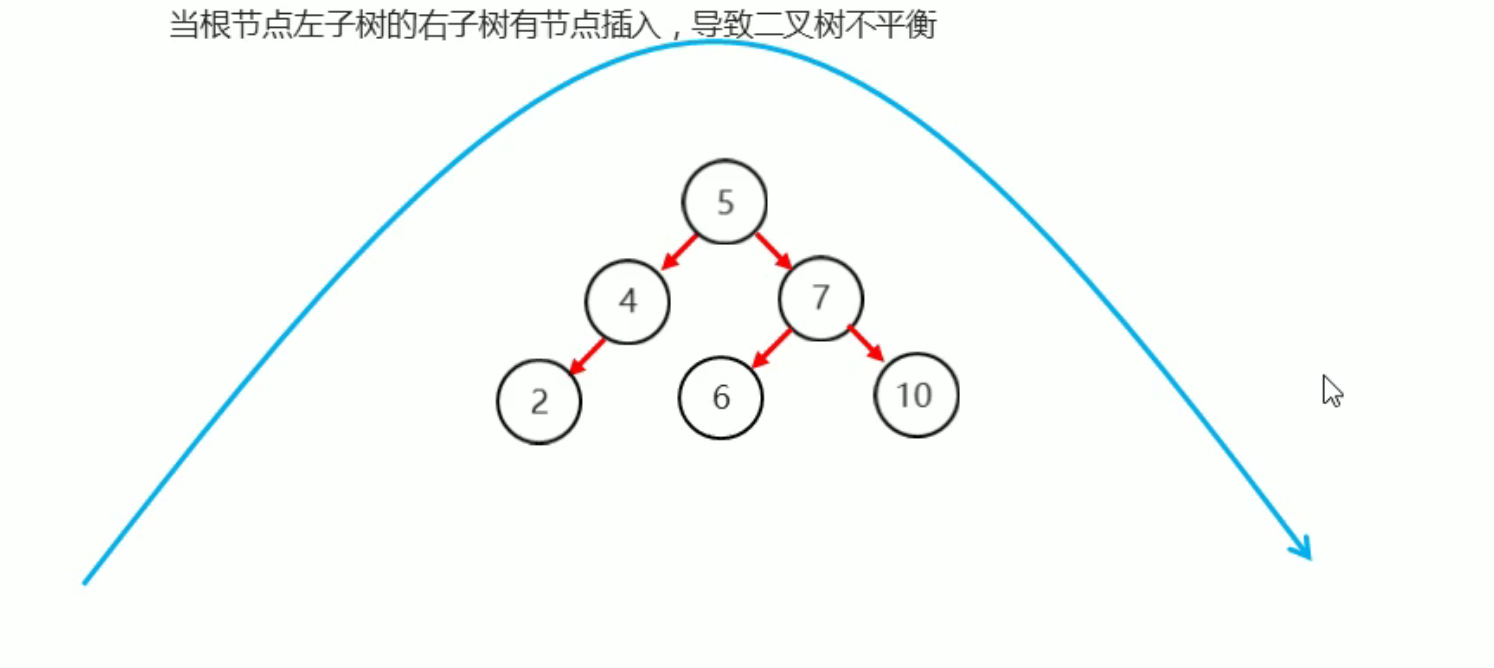
当根节点左子树的右子树有节点插入,导致二叉树不平衡

我们发现单单靠一次的右旋是无法恢复平衡状态

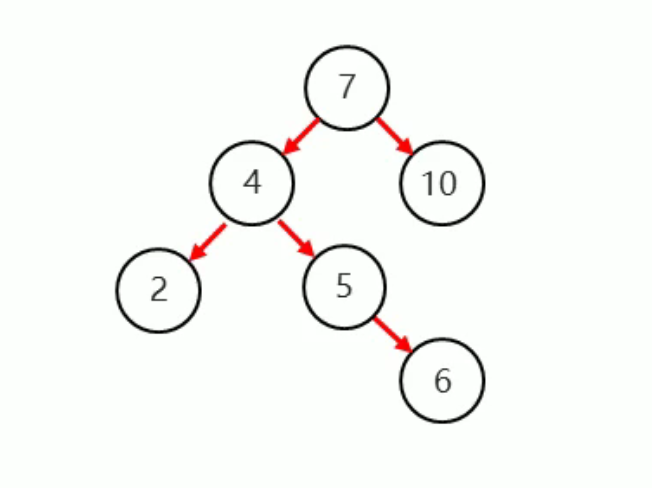
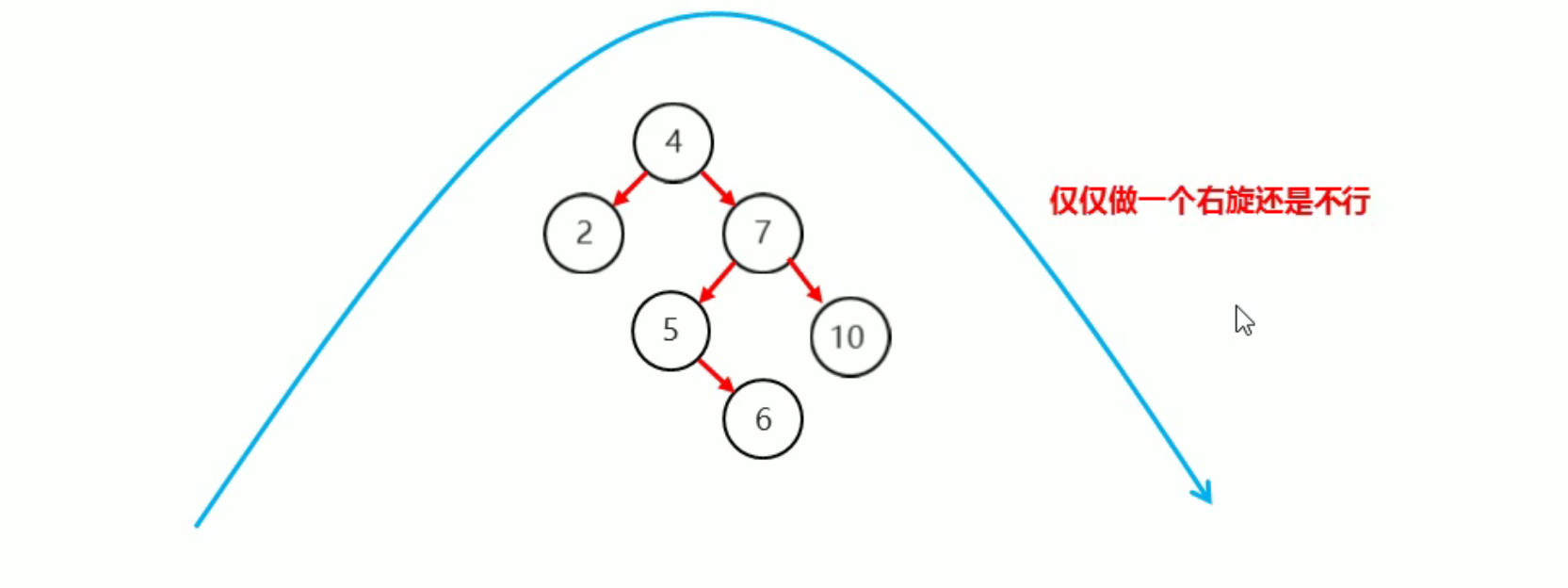
我们需要将5当为根节点 左旋一次

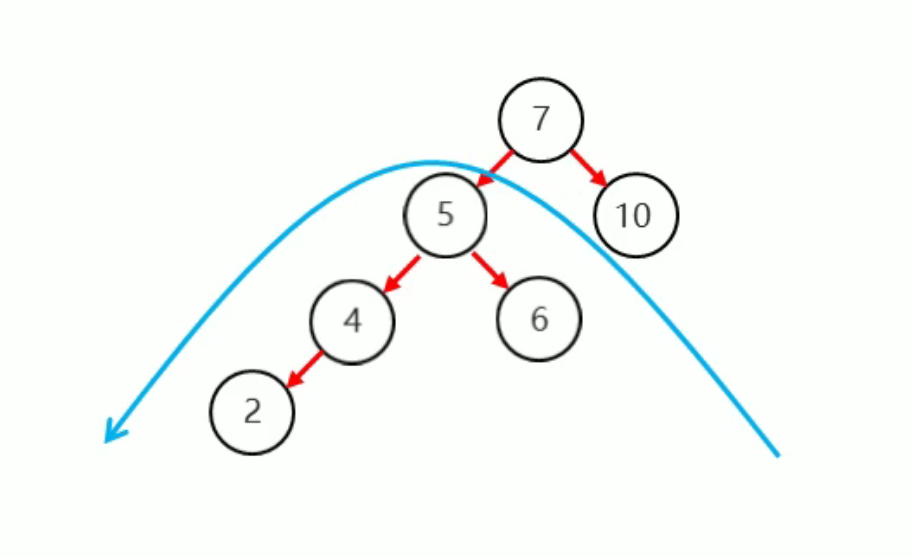
再由根节点7 右旋一次

4.2.2. 右右

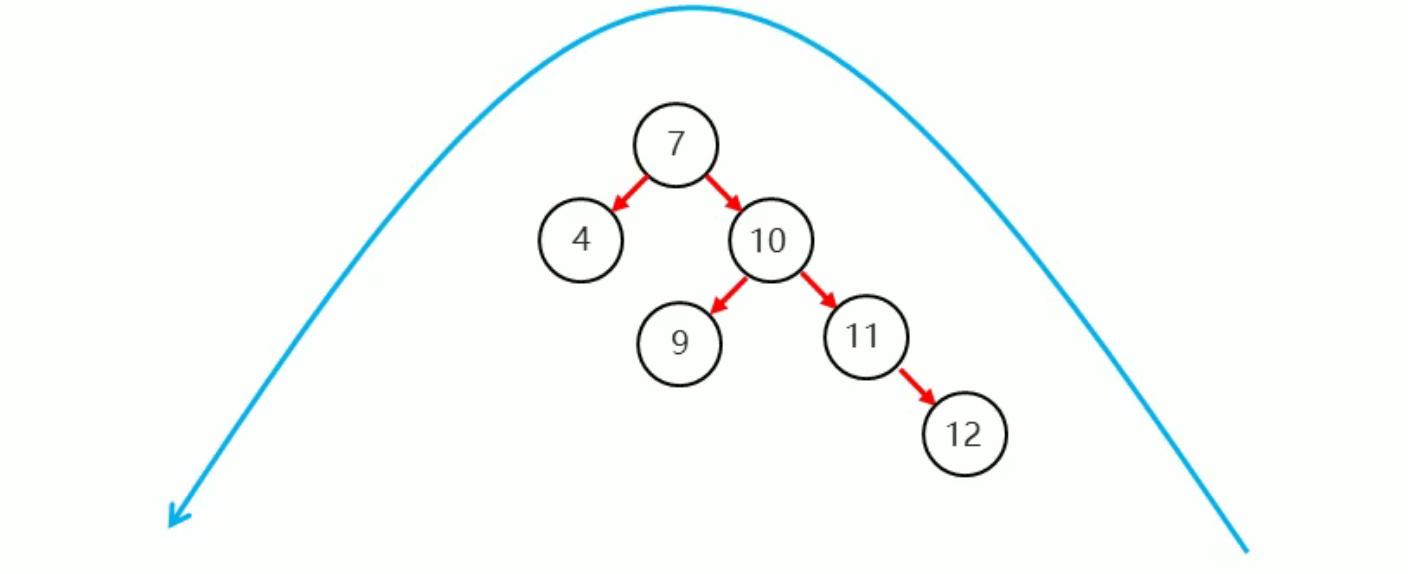
当根节点右子树的右子树有节点插入,导致二叉树不平衡

我们只需要将此二叉树左旋既可

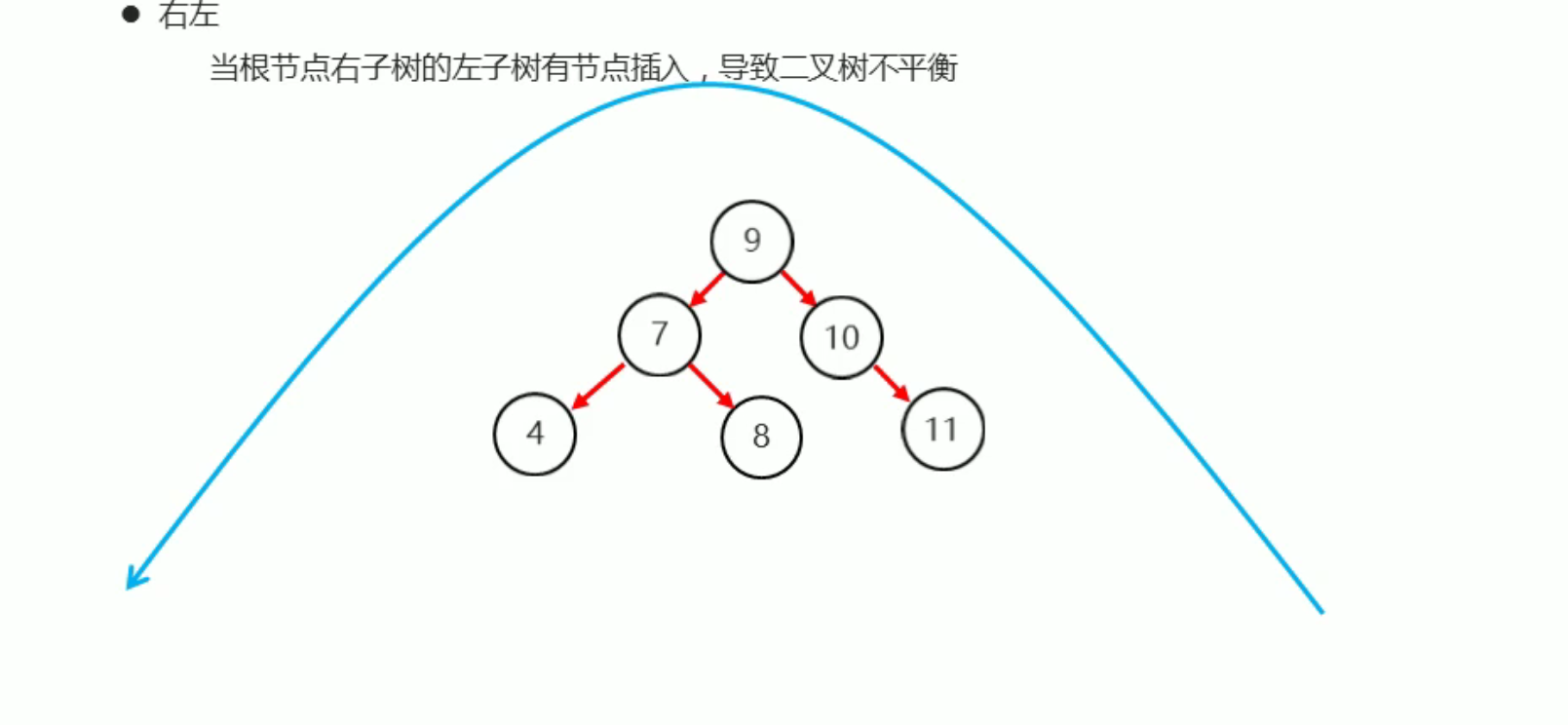
4.2.4. 右左

当根节点右子树的左子树有节点插入,导致二叉树不平衡

我们发现单单靠一次的左旋是无法恢复平衡状态

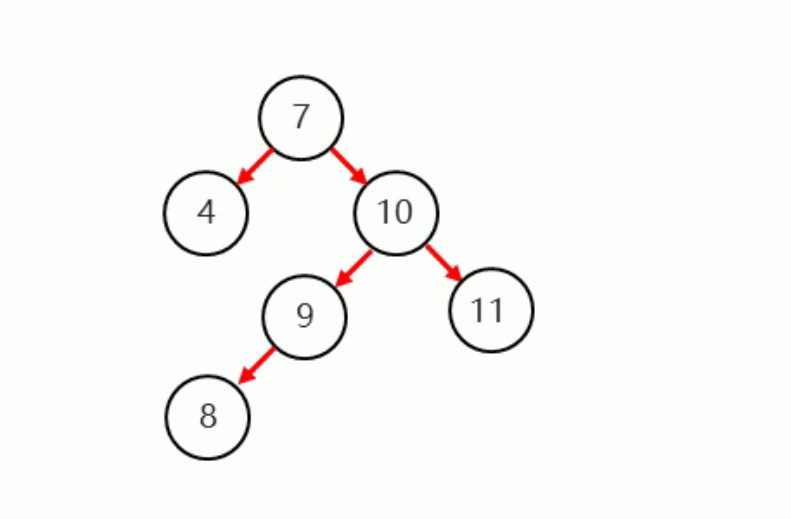
把10当为根节点,右旋一次

再以根节点 左旋

5. 红黑树

红黑树又称平衡二叉B树

它是一种特色的二叉查找树,红黑树的每个节点上都有存储位表示节点的颜色

每一个节点可以是红或黑;红黑树不是高度平衡的,它的平衡是通过”红黑规则”进行实现的

而平衡二叉树是高度平衡的,当左右子树高度差超过1时则触发旋转

而红黑树是根据定于的红黑规则触发旋转的

5.1. 红黑规则

1. 每一个节点或是红色,或者是黑色
2. 根节点必须是黑色
3. 如果一个节点没有子节点或者父节点,则该节点相应的指针属性值为Nil,这些Nil视为叶节点,每个叶节点(Nil)是黑色的
4. 如果某个节点是红色的,那么它的子节点必须是黑色(不能出现两个红色节点相连的情况)
5. 对每个节点,从该节点到其所有后代节点的简单路径上,均包含相同数目的黑色节点

3.1. 添加节点

添加节点时,默认为红色,效率比为黑色要高

并遵循二叉查找树的规则

5.2.1. 当父节点也是红色,叔叔节点也是红色

因为默认是添加红色,如果父节点为红色,叔叔节点也为红色

1. 父节点改为黑色
2. 叔叔(祖父节点的左/右子节点)节点改为黑色
3. 将祖父节点改为红色
4. 如果祖父节点为根节点则重新变回黑色

5.2.2. 当父节点也是红色,叔叔节点是黑色

1. 将父节点改为黑色
2. 将祖父节点改为红色

3. 以祖父节点为支点进行旋转

   • 左节点大于则右旋
   • 右节点大于则左旋
   • 可以把Nil先忽略,旋转完后再加回叶节点,比较好理解

5.3. 总结

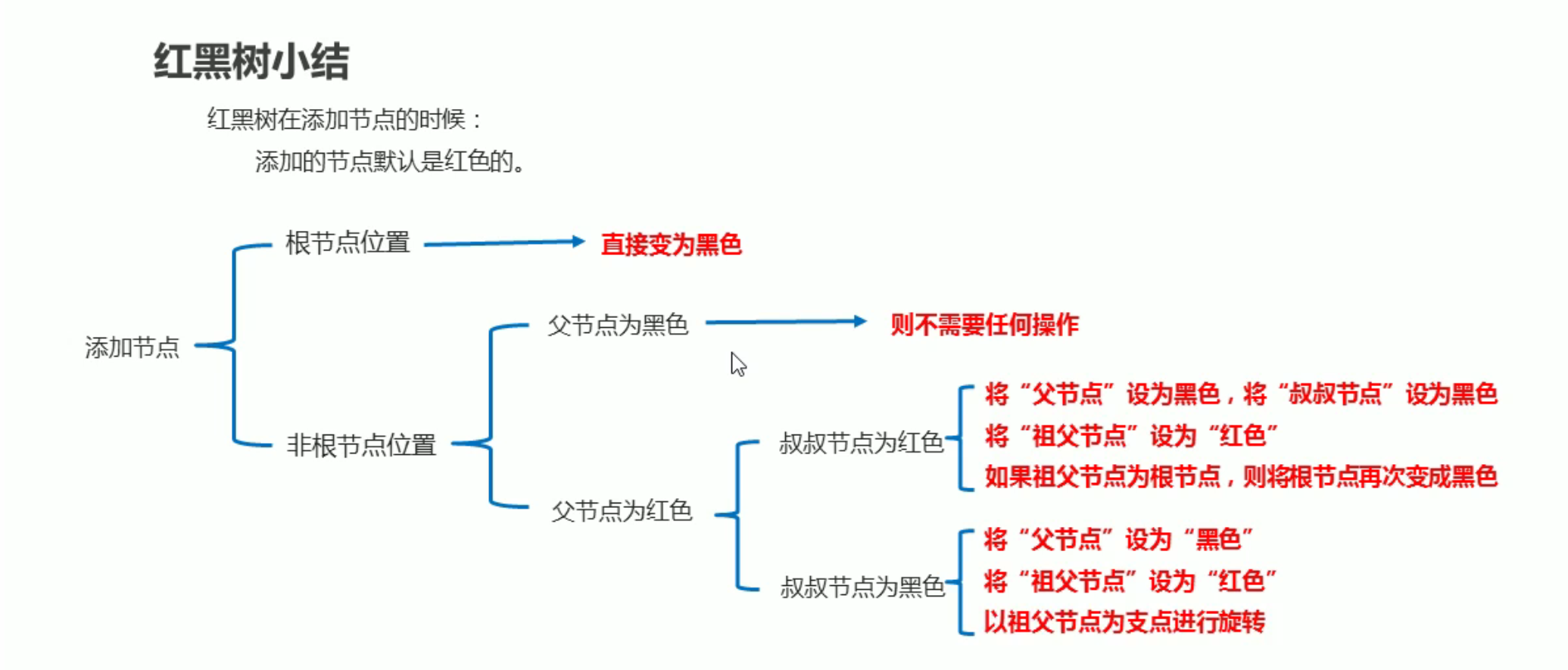
6. TreeSet遍历

先获取左边,再获取中间,再获取右边