训练题：最长公共子串

题目：http://t.cn/A6VAyutk

  2. string LCS( string str1, string str2 )
  3. {
  4.     if( str1 == "" || str2 == "" ) { return ""; }
  6.     const auto size1 = str1.size();
  7.     const auto size2 = str2.size();
  8.     map<char, vector<int>> dataMap;
  10.     for( int idx1 = 0; idx1 < size1; ++idx1 ) { dataMap[str1[idx1]].push_back( idx1 ); }
  12.     int maxLen = 0, startIdx = -1;
  13.     for( int idx2 = 0, tmpCount = 0; idx2 < size2; ++idx2 )
  14.     {
  15.         if( dataMap.count( str2[idx2] ) )
  16.         {
  17.             for( auto &idx1 : dataMap[str2[idx2]] )
  18.             {
  19.                 tmpCount = 1;
  20.                 for( ; idx1 + tmpCount < size1 && idx2 + tmpCount < size2 && str1[idx1 + tmpCount] == str2[idx2 + tmpCount]; ++tmpCount );
  21.                 if( tmpCount > maxLen )
  22.                 {
  23.                     startIdx = idx1;
  24.                     maxLen = tmpCount;
  25.                 }
  26.             }
  27.         }
  28.     }
  29.     if( !maxLen ) { return ""; }
  30.     return str1.substr( startIdx, maxLen );
  31. }

训练题：最长回文子串

题目：http://t.cn/Eq0YD3Q

方法一：动态规划

  • 空间复杂度：O(n2)
  • 时间复杂度：O(n2)

dp[i][j]指子串[i~j]是否为回文串。有如下动态公式：
算法训练_动态规划 - 图1

  2. string longestPalindrome( string s )
  3. {
  4.     if( s.size() < 2 ) { return s; }
  6.     const short size = s.size();
  7.     short maxLen      = -1;
  8.     short maxBeginIdx = -1;
  10.     vector<vector<bool>> dataMap( size, vector<bool>( size ) );
  12.     // 根据动态规划公式，我们应该先找出端的回文串，再此基础上才能确定更长的串
  13.     // 因此遍历方式应该是：
  14.     //        1、遍历字符串中的所有子串
  15.     //        2、先遍历短的子串
  16.     for( short interval = 0; interval < size; ++interval )        // 遍历首尾间隔为interval的子串
  17.     {
  18.         // left，right为子串的首尾索引
  19.         for( short left = 0, right = -1; left < size; ++left )
  20.         {
  21.             right = left + interval;
  22.             if( right > size - 1 ) { break; }
  24.             if( left == right ) { dataMap[left][right] = true; }    // 单个字符肯定是回文
  25.             else if( right - left == 1 )                            // 2个字符串只有相同才是回文
  26.             {
  27.                 dataMap[left][right] = s[left] == s[right];
  28.             }
  29.             else                                                    // 动态规划公式
  30.             {
  31.                 dataMap[left][right] = dataMap[left + 1][right - 1] && s[left] == s[right];
  32.             }
  34.             // 保存当前最长的回文串
  35.             if( dataMap[left][right] && maxLen < right - left + 1 )
  36.             {
  37.                 maxLen = right - left + 1;
  38.                 maxBeginIdx = left;
  39.             }
  40.         }
  41.     }
  43.     return s.substr( maxBeginIdx, maxLen );
  44. }

方法二：中心扩展算法

  2. string longestPalindrome( string s )
  3. {
  4.     if( s.size() < 2 ) { return s; }
  6.     const short size = s.size();
  7.     short maxLen = 0;
  8.     short maxLeftIdx = 0;
  10.     // 遍历找出以idx或者idx，idx+1为中心的最长回文长度。
  11.     for( short idx = 0, len1 = -1, len2 = -1, len3 = -1; idx < size; ++idx )
  12.     {
  13.         len3 = std::max( expand( s, size, idx, idx ), expand( s, size, idx, idx + 1 ) );
  14.         if( len3 > maxLen )
  15.         {
  16.             maxLen = len3;
  17.             maxLeftIdx = idx - ( ( len3 - 1 ) >> 1 );
  18.         }
  19.     }
  20.     return s.substr( maxLeftIdx, maxLen );
  21. }
  23. // left~right之间是回文，向两边扩展，找出最长的回文。
  24. short expand( const string &s, const short &size, short left, short right )
  25. {
  26.     for( ; left >= 0 && right < size && s[left] == s[right]; --left, ++right );
  27.     return right - left - 1;
  28. }

训练题：N个骰子点数

题目：https://leetcode-cn.com/problems/nge-tou-zi-de-dian-shu-lcof/

  • 1、定义dp[i]或者dp[i][j]

算法训练_动态规划 - 图2

  • 2、找出转移方程

算法训练_动态规划 - 图3

  • 第i个骰子投出点数为1的次数 = 算法训练_动态规划 - 图4
  • 第i个骰子投出点数为2的次数 = 算法训练_动态规划 - 图5
  • ……
  • 第i个骰子投出点数为6的次数 = 算法训练_动态规划 - 图6

这六种情况之和就是dp[i][j]的所有可能情况。

  • 3、边界条件

算法训练_动态规划 - 图7
即第1个骰子投出各个点数的次数。

1、递归实现

  • 时间复杂度：O（6n），实现简单，但是非常低效，因为有大量重复计算。
  • 空间复杂度：O（n2）
  2. vector<double> dicesProbability(int n) {
  4.     vector<double> ret;
  6.     // 投n个骰子的全排列。
  7.     double totalCount = pow(6.0, n);
  9.     // 投n个骰子的总点数范围
  10.     for(int i = 1*n; i <= 6*n; ++i) {
  11.         ret.push_back( fuck(n, i) / totalCount );
  12.     }
  14.     return ret;
  15. }
  17. int fuck( int i, int j ) {
  18.     if(i == 1){
  19.         if(j >= 1 && j <= 6) return 1;
  20.         return 0;
  21.     }
  22.     return fuck(i-1, j-1) + fuck(i-1, j-2) + fuck(i-1, j-3) +
  23.            fuck(i-1, j-4) + fuck(i-1, j-5) + fuck(i-1, j-6);
  24. }

2、优化计算

  • 改成迭代
  • 保存状态记录 ```cpp

vector dicesProbability(int n) {

  1. if(n < 1 || n > 11) return {0};
  3. vector<double> ret;
  4. double totalCount = pow(6, n);
  6. // dp[i][j]
  7. int dp[12][67] = {0};
  9. for(char i = 1; i <= 6; ++i) dp[1][i] = 1;
  11. // i，j就是指dp[i][j]的i、j
  12. for(char i = 2; i <= n; ++i) {
  13.     for(char j = i; j <= 6*i; ++j) {
  14.         for(char cur = 1; cur <=6; ++cur){
  15.                 if(j > cur) dp[i][j] += dp[i-1][j-cur];
  16.             }
  17.     }
  18. }
  19. ret.reserve(5*n+1);
  20. for(char i = n; i <= 6*n; ++i) ret.push_back(dp[n][i] / totalCount);
  21. return ret;

}

  1. <a name="QMqj6"></a>
  2. ## 3、优化空间
  3. ```cpp
  5. vector<double> dicesProbability( int n )
  6. {
  7.     if( n < 1 || n > 11 ) return{ 0 };
  9.     vector<double> ret;
  10.     double totalCount = pow( 6, n );
  12.     // 如果当前循环是第n轮，则dp保存的是n-1轮的结果，这是可以通过dp的数据更新自己为n轮的数据。
  13.     int dp[67] = { 0 };
  15.     for( char i = 1; i <= 6; ++i ) { dp[i] = 1; }
  17.     for( char i = 2; i <= n; ++i )
  18.     {
  19.         // 从后往前更新，避免把还需要用到的数据覆盖。
  20.         for( char j = 6 * i; j >= i; --j )
  21.         {
  22.             //         1 2 3 4 5 6  7  8  9  10  11  12 13 14 15 16 17 18
  23.             // i=1     1 1 1 1 1 1
  24.             // i=2       1 2 3 4 5  6  5  4  3   2   1
  25.             // i=3         1 3 6 10 15 21 25 27  27  25 21 15 10 6  3  1
  26.             dp[j] = 0;
  27.             for(char cur = 1; cur <= 6; ++cur){
  28.                 if(j - cur + 1 >= i) dp[j] += dp[j - cur];
  29.             }
  30.         }
  31.     }
  32.     ret.reserve( 5 * n + 1 );
  33.     for( char i = n; i <= 6 * n; ++i ) { ret.push_back( dp[i] / totalCount ); }
  34.     return ret;
  35. }

训练题：股票最大利润

题目：http://t.cn/A65Jyf61

  2. int maxProfit(vector<int>& prices) {
  3.     if(prices.size() < 2) return 0;
  5.     int profitMax = 0;
  6.     const auto days = prices.size();
  7.     for(int dayIdx = 1, lastProfitMax = 0; dayIdx < days; ++dayIdx)
  8.     {
  9.         lastProfitMax = max(prices[dayIdx] - prices[dayIdx - 1] + lastProfitMax, 0);
  10.         profitMax = max(profitMax, lastProfitMax);
  11.     }
  13.     return profitMax;
  14. }

训练题：丑数

题目：http://t.cn/A6VM1wMb

算法训练_动态规划 - 图8算法训练_动态规划 - 图9

其中p2、p3、p5满足以下条件：

算法训练_动态规划 - 图10

  2. int nthUglyNumber( int n )
  3. {
  4.     vector<int> nums( n + 1, 1 );
  6.     int p2 = 1, p3 = 1, p5 = 1;
  8.     for( int i = 2; i <= n; ++i )
  9.     {
  10.         int a1 = nums[p2] * 2;
  11.         int b1 = nums[p3] * 3;
  12.         int c1 = nums[p5] * 5;
  14.         nums[i] = std::min( std::min( a1,  b1 ), c1 );
  16.         // 求出第i个丑数之后，要及时更新p2、p3、p5
  17.         nums[i] == a1 && ++p2;
  18.         nums[i] == b1 && ++p3;
  19.         nums[i] == c1 && ++p5;
  20.     }
  22.     return nums[n];
  23. }

训练题：最多礼物（最优路径）

题目：http://t.cn/A6qoF5qK

求最值，首先考虑动态规划。

动态规划的核心思想：

  • 递归化（迭代化）
    • dp[i][j]，到坐标（i, j）的最大礼物值，这个提炼是否正确，就看下面这一条是否可行。
  • 前一步的结果作为下一步的参考
    • dp[i][j] = max(dp[i-1][j], dp[i][j-1]) + val[i][j]，坐标（i，j）的最大礼物值取决于左边和上方更大值者。
    • 注意考虑i-1和j-1的边界情况。
  • 选择遍历方式
    • 使得可以先计算前面的dp，再计算后面的dp。
    • 这一题，情况简单，从左往右，从上往下遍历就满足这个要求。 ```cpp

int maxValue(vector>& grid) {

  1. if(grid.empty() || grid[0].empty()) return -1;
  3. const auto m = grid.size();
  4. const auto n = grid[0].size();
  6. // 这两个循环先求出第一行/列的dp值，免得在下面的双重循环中多次判断
  7. for(int col = 1; col < n; ++col) grid[0][col] += grid[0][col-1];
  8. for(int row = 1; row < m; ++row) grid[row][0] += grid[row-1][0];
  10. for(int row = 1; row < m; ++row){
  11.     for(int col = 1; col < n; ++col){
  12.         grid[row][col] += max(grid[row-1][col], grid[row][col-1]);
  13.     }
  14. }
  16. return grid[m-1][n-1];

}

  1. <a name="yBvv3"></a>
  2. # 训练题：跳台阶
  3. 题目：[http://t.cn/A6Vz29oQ](http://t.cn/A6Vz29oQ)
  4. <a name="vS67K"></a>
  5. ## 方法一：最简单递归
  7. - 时间复杂度：O(n2)
  8. - 空间复杂度：递归栈空间。
  9. - 极其简单，效率极其低下
  10. ```cpp
  12. int jumpFloor( int number )
  13. {
  14.     if( number < 3 ) { return number; }
  16.     return jumpFloor( number - 1 ) + jumpFloor( number - 2 );
  17. }

方法二：记忆存储

保存递归过的结果，减少递归次数。

  • 时间复杂度：O(n)
  • 空间复杂度：O(n) + 递归栈空间。 ```cpp

int jumpFloor( int number ) { if( number < 4 ) { return number; }

  1. // 45个数初始化为-1，超过45，int会溢出。
  2. // index：对应number，value对应跳法数
  3. vector<int> shit( 45, -1 );
  5. return _jumpFloor( number - 1, shit ) + _jumpFloor( number - 2, shit );

} int _jumpFloor( int number, vector &shit ) { if( number < 4 ) { return number; } if( shit[number] != -1 ) { return shit[number]; } return shit[number] = _jumpFloor( number - 1, shit ) + _jumpFloor( number - 2, shit ); }

  1. <a name="Cwdzt"></a>
  2. ## 方法三：自底向上
  3. 斐波那契数列从前往后叠加，直到目的位置。
  5. - 时间复杂度：O(n)
  6. - 空间复杂度：O(1)
  7. ```cpp
  9. int jumpFloor( int number )
  10. {
  11.     if( number < 4 ) { return std::max( number, 0 ); }
  12.     for( int a = 1, b = 2, tmp, step = 3;; step++ )
  13.     {
  14.         tmp = b;
  15.         b = a + b;
  16.         a = tmp;
  17.         if( step == number ) { return b; }
  18.     }
  19. }

训练题：斐波那契数列求值

题目：http://t.cn/A6VziaJb
和上情形本质完全一样，这里就采用第三种方法：

  2. int Fibonacci(int n) {
  3.     if(n < 2) return n;
  4.     int b = 1;
  5.     for(int a = 1, tmp; n > 2; n--){
  6.         tmp = b;
  7.         b = tmp + a;
  8.         a = tmp;
  9.     }
  10.     return b;
  11. }

训练题：最大累加和

语雀内容

训练题：数字组合

语雀内容

训练题：最长递增子序列（LIS）

题目：https://leetcode-cn.com/problems/longest-increasing-subsequence/

动态规划（递归版）

  2. int lengthOfLIS(vector<int>& nums) {
  3.     if(nums.size() < 2) return nums.size();
  5.     const auto size = nums.size();
  6.     int ret = 0;                  
  8.     // 定义dp：dp[i]为以nums[i]结尾的最长子序列长度
  9.     vector<int> dp(size, -1);
  11.     for(int idx = 0; idx < size; ++idx)
  12.         // ret = max(dp[i])，0 <= i <= idx。
  13.         ret = max(ret, maxLenOfLIS(nums, dp, idx));
  15.     return ret;
  16. }
  18. // 以idx索引处字符结尾的最长子序列长度，dp是为了保存迭代状态
  19. // dp[i] = max(dp[j]+1)，其中0 <= j < i，且dp[j] < dp[i]（这样才能做到以nums[i]结尾）
  20. int maxLenOfLIS(vector<int>& nums, vector<int>& dp, int idx){
  21.     if(idx == 0) return 1;
  22.     if(dp[idx] != -1) return dp[idx];
  24.     dp[idx] = 1;
  25.     for(int tmp = 0; tmp < idx; ++tmp){
  26.         // dp[idx] = max(dp[i]+1)，其中0 <= i < idx，且nums[i] < nums[idx]。
  27.         // 因为必须要以nums[idx]结尾,则dp[i]的结尾字符值必须小于nums[idx]
  28.         if(nums[tmp] < nums[idx]) dp[idx] = max(dp[idx], maxLenOfLIS(nums, dp, tmp) + 1);
  29.     }
  31.     return dp[idx];
  32. }

动态规划（迭代版）

  2. // 迭代版相对于递归版，少了递归栈空间。
  3. // 低索引的计算数据用于高索引的计算。
  4. int lengthOfLIS(vector<int>& nums) {
  5.     if(nums.size() < 2) return nums.size();
  7.     const auto size = nums.size();
  8.     int ret = 1;
  9.     vector<int> dp(size, 1);   // key:idx, value:maxLen
  11.     for(int idx = 1, tmp; idx < size; ++idx)
  12.     {
  13.         for(tmp = 0; tmp < idx; ++tmp){
  14.             if(nums[tmp] < nums[idx]){
  15.                 dp[idx] = max(dp[idx], dp[tmp] + 1);
  16.             }
  17.         }
  18.         ret = max(ret, dp[idx]);
  19.     }
  21.     return ret;
  22. }

动态规划（贪心）

考虑一

动态规划的本质就是穷举，将所有子问题解决进而得到问题的最优解。
贪心算法的思想是每一步取子问题的最优解，迭代进而得到问题的最优解。

上面动态规划中的转移方程并不是最优解：
转移方程：算法训练_动态规划 - 图11。
我们在找这个max值的时候是线性遍历的方式寻找（复杂度n），即从头到尾遍历。key值i为字符索引与序列长度大小没有任何关系。假设我们以序列长度作为key值，那最大key就是最大长度。

考虑二

我们要使上升子序列尽可能的长，则我们需要让序列上升得尽可能慢，因此我们希望每次在上升子序列最后加上的那个数尽可能的小。

算法训练_动态规划 - 图12

  2. int lengthOfLIS(vector<int>& nums) {
  3.     if(nums.size() < 2) return nums.size();
  5.     const auto size = nums.size();
  6.     vector<int> dp(size+1);   // 长度为idx的子序列的最小结尾字符。
  8.     dp[1] = nums[0];          // 起始状态，长度为1的子序列的结尾字符是首字符。
  10.     int tmpLenIdx = 1;                    // tmpLenIdx表示minCharOfLen的有效长度，即
  11.     for(int idx = 1; idx < size; ++idx)
  12.     {
  13.         // 1  4  5  2  3  4  5  6
  14.         //       ^   
  15.         // curr dp: 1  4
  16.         // next dp: 1  4  5
  17.         if(nums[idx] > dp[tmpLenIdx]) {
  18.             minCharOfLen[++tmpLenIdx] = nums[idx];
  19.         }
  20.         else{
  22.             // 1  4  5  2  3  4  5  6
  23.             //          ^
  24.             // curr dp: 1  4  5
  25.             // next dp: 1  2  5
  27.             // 二分叉查找法，查找到第一个大于2的val值，并更新它。
  28.             // 这里的实际意义指长度为2的递增子序列的最小结尾字符更新为2
  29.             int left = 1;
  30.             for(int right = tmpLenIdx, mid; left < right;){
  31.                 mid = left + ((right - left) >> 1);
  33.                 if(dp[mid] < nums[idx]) left = mid + 1;
  34.                 else if(dp[mid] >= nums[idx]) right = mid;
  35.             }
  37.             dp[left] = nums[idx];
  38.         }
  39.     }
  41.     return tmpLenIdx;
  42. }

训练题：最长递增子序列个数

题目：https://leetcode-cn.com/problems/number-of-longest-increasing-subsequence/

  2. int findNumberOfLIS( vector<int> &nums )
  3. {
  4.     if( nums.size() < 2 ) { return nums.size(); }
  6.     const auto size = nums.size();
  8.     vector<int> dp( size, 1 );        // 以nums[i]结尾的LIS长度
  9.     vector<int> count( size, 1 );     // 以nums[i]结尾的LIS个数
  11.     dp[0] = 1;                      // 初始状态
  12.     count[0] = 1;                   // 初始状态
  13.     int maxLen = 0;
  14.     int maxLenCount = 0;
  16.     for( int idx = 1; idx < size; ++idx )
  17.     {
  18.         for( int tmp = 0; tmp < idx; ++tmp )
  19.         {
  20.             if( nums[idx] > nums[tmp] ) {           // 统计递增子序列。
  21.                 if( dp[tmp] + 1 > dp[idx] ) {       // 出现更长的最长递增子序列
  22.                     dp[idx] = dp[tmp] + 1;
  23.                     count[idx] = count[tmp];
  24.                 }
  25.                 else if( dp[tmp] + 1 == dp[idx] ) { // 找到同样长的最长递增子序列。
  26.                     count[idx] += count[tmp];
  27.                 }
  28.             }
  29.         }
  30.         maxLen = max(maxLen, dp[idx]);
  31.     }
  33.     for( int idx = 0; idx < size; ++idx )
  34.         if( maxLen == dp[idx] ) maxLenCount += count[idx];
  36.     return maxLenCount;
  37. }

训练题：“俄罗斯套娃”信封

题目：https://leetcode-cn.com/problems/russian-doll-envelopes/

方法一：动态规划

时间复杂度：O（n）

  2. int maxEnvelopes( vector<vector<int>> &envelopes )
  3. {
  4.     if( envelopes.size() < 2 ) { return envelopes.size(); }
  6.     // 宽度升序排列，高度降序排列。升序排列好理解，降序排列的原因是考虑宽度相同的情况。
  7.     sort( envelopes.begin(), envelopes.end(), []( const vector<int> &a, const vector<int> &b )
  8.          {
  9.              return a[0] < b[0] || ( a[0] == b[0] && a[1] > b[1] );
  10.          } );
  12.     const auto size = envelopes.size();
  13.     vector<int> dp( size, 1 );        // dp[i]，以第i个信封结尾的套娃数量最大长度。
  14.     int ret = 1;
  16.     for( int idx = 1; idx < size; ++idx )
  17.     {
  18.         for( int tmp = 0; tmp < idx; ++tmp)
  19.         {
  20.             // 这里只比较了高度，为什么就可以呢？
  21.             // 首先可以肯定，envelopes[idx] >= envelopes[tmp][0]的，分两种情况分析：
  22.             // 假设envelopes[tmp][0] == envelopes[idx]，则envelopes[idx][1] <= envelopes[tmp][1]，
  23.             //      envelopes[idx][1] > envelopes[tmp][1]不可能成立。也即宽度相同时候，这个if不可能成立，显然宽度相同不能进行套娃，因此这天然帮我们过滤了宽度相同的情况。
  24.             // 假设envelopes[tmp][0] < envelopes[idx]，显然只需要判断高度即可，即如下判断。
  25.             // 综上，宽度升序，高度降序时，以下条件判断即可过滤出idx可套娃tmp的情况。
  26.             if( envelopes[tmp][1] < envelopes[idx][1] )
  27.             {
  28.                 dp[idx] = max( dp[idx], dp[tmp] + 1 );  // 找到套娃最大值。
  29.                 ret = max( ret, dp[idx] );
  30.             }
  31.         }
  32.     }
  34.     return ret;
  35. }

方法二：贪心算法

和最长递增子序列类似的贪心。

  2. int maxEnvelopes(vector<vector<int>>& envelopes) {
  3.     if(envelopes.size() < 2) return envelopes.size();
  5.     sort(envelopes.begin(), envelopes.end(), [](const vector<int>& a, const vector<int>& b){
  6.         return a[0] < b[0] || (a[0] == b[0] && a[1] > b[1]);
  7.     });
  9.     const auto size = envelopes.size();
  10.     vector<int> dp = { envelopes[0][1] };        // dp[i]，套娃信封数量为i+1的最小结尾信封索引
  12.     dp.reserve(envelopes.size());
  14.     for(int idx = 1; idx < size; ++idx){
  16.         int height = envelopes[idx][1];
  18.         if(height > dp.back()){        // 后面的height大于前面的height，则后面的width肯定是大于前面的width
  19.             dp.push_back(height);
  20.         }
  21.         else{
  22.             auto it = lower_bound(dp.begin(), dp.end(), height);    
  23.             *it = height;
  24.         }
  25.     }
  27.     return dp.size();
  28. }

训练题：最大乘积子数组

题目：https://leetcode-cn.com/problems/maximum-product-subarray/

  • 时间复杂度：O（n）
  • 空间复杂度：O（n）

由于乘法的负负得正的特性，越小的负数乘以一个负数结果会越大，越大的正数乘以一个正数结果也会越大。我们可以记录两个极值，最小乘积和最大乘积，这两个乘积因为负数的出现会调换位置，当然还有0。

算法训练_动态规划 - 图13

  2. int maxProduct(vector<int>& nums) {
  4.     if(nums.empty()) return 0;
  5.     if(nums.size() == 1) return nums[0];
  7.     const auto size = nums.size();
  8.     int ret = 0;
  10.     vector<int> dp_max(size, 0);
  11.     vector<int> dp_min(size, 0);
  13.     ret = dp_max[0] = dp_min[0] = nums[0];
  15.     for(int idx = 1; idx < size; ++idx){
  17.         dp_max[idx] = max(dp_max[idx-1]*nums[idx], max(nums[idx], dp_min[idx-1]*nums[idx]));
  18.         dp_min[idx] = min(dp_max[idx-1]*nums[idx], min(nums[idx], dp_min[idx-1]*nums[idx]));
  20.         ret = max(ret, dp_max[idx]);
  21.     }
  23.     return ret;
  24. }

把O（n）空间优化为O（1），dp[i]只需要dp[i-1]的数据。

  2. int maxProduct(vector<int>& nums) {
  4.     if(nums.empty()) return 0;
  5.     if(nums.size() == 1) return nums[0];
  7.     const auto size = nums.size();
  8.     int ret         = nums[0];
  9.     int dp_max      = nums[0];
  10.     int dp_min      = nums[0];
  12.     for(int idx = 1, dp_tmp; idx < size; ++idx){
  14.         dp_tmp = dp_max;
  15.         dp_max = max(dp_max*nums[idx], max(nums[idx], dp_min*nums[idx]));
  16.         dp_min = min(dp_tmp*nums[idx], min(nums[idx], dp_min*nums[idx]));
  18.         ret = max(ret, dp_max);
  19.     }
  21.     return ret;
  22. }

训练题：环形子数组的最大和

题目：https://leetcode-cn.com/problems/maximum-sum-circular-subarray/

共有两种情况：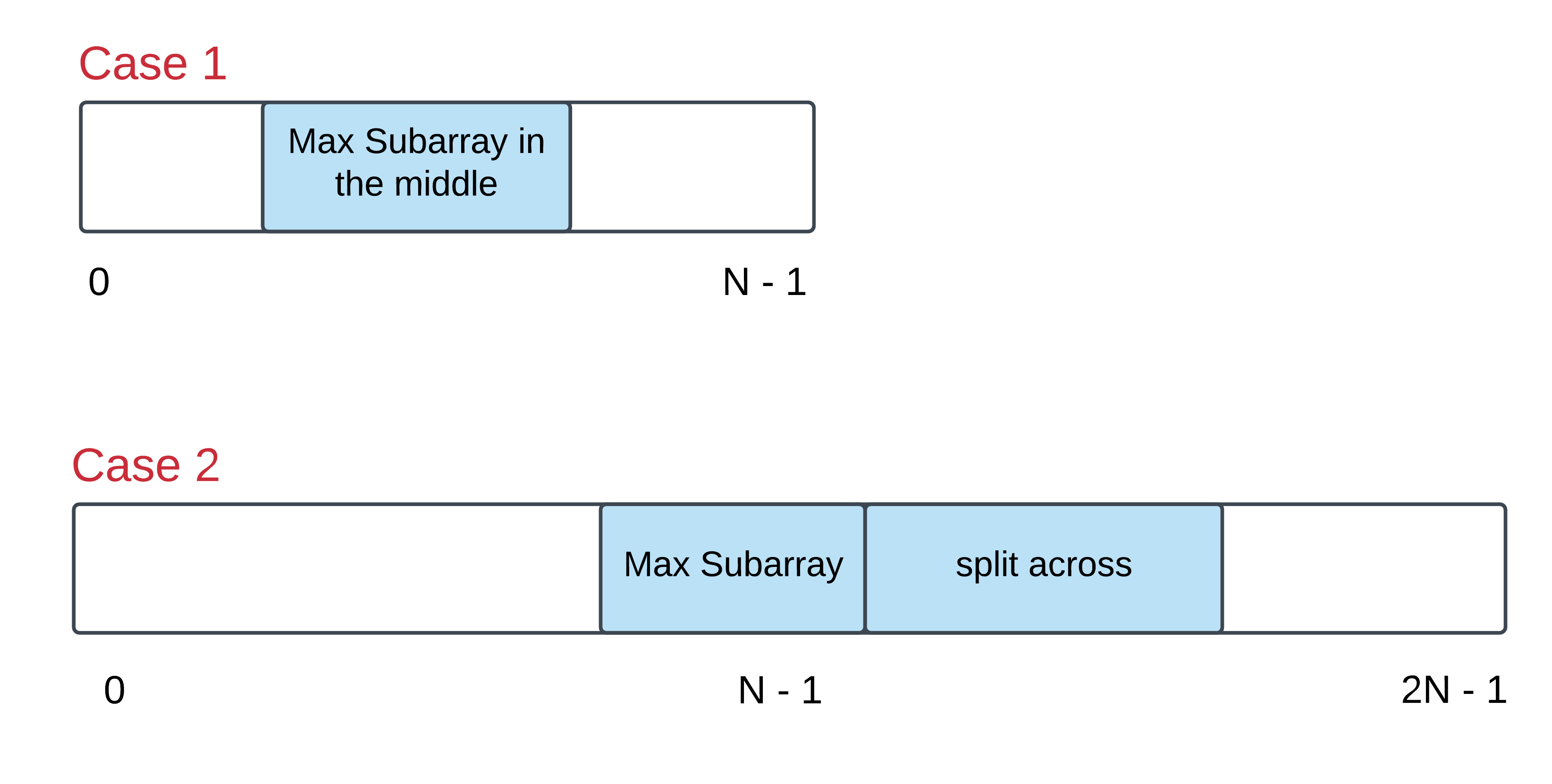
算法训练_动态规划 - 图14
蓝色区域为最大和的连续子数组。
情况一：该连续子数组没有同时包含首尾元素，经没有across的情况，就是求最大子序和的问题。
情况二：该连续子数组同时包含了首尾元素，此时该区域在数组上是在首尾两端两部分组成，我们只需求得中间连续部分的最小子序和，即可获得最大和。
算法训练_动态规划 - 图15

  2. int maxSubarraySumCircular(vector<int>& nums) {
  4.     if(nums.empty()) return 0;
  5.     if(nums.size() == 1) return nums[0];
  7.     const auto size = nums.size();
  9.     int sum     = nums[0];        // 数组和
  10.     int sum_max = nums[0];        // 情况一的最大子序和
  11.     int sum_tmp = nums[0];        // 中间变量
  12.     for(int idx = 1; idx < size; ++idx){
  13.         sum += nums[idx];
  14.         sum_tmp = nums[idx] + max(sum_tmp, 0);
  15.         sum_max = max(sum_max, sum_tmp);
  16.     }
  18.     int sum_min = nums[1];        // 情况二的最小子序和
  19.     sum_tmp = nums[1];
  21.     // 情况二的最大子序和肯定包含了nums[0]和nums[size-1]
  22.     // 因此最小子序和肯定在nums[1]~nums[size-2]区间。
  23.     for(int idx = 2; idx < size - 1; ++idx){
  24.         sum_tmp = nums[idx] + min(sum_tmp, 0);
  25.         sum_min = min(sum_min, sum_tmp);
  26.     }
  28.     return max(sum_max, sum - sum_min);
  29. }

训练题：最大子矩阵（待完成）

题目：https://leetcode-cn.com/problems/max-submatrix-lcci/

训练题：Nim游戏

题目：https://leetcode-cn.com/problems/nim-game/

  2. bool canWinNim(int n) {
  4.     // 余子数量为n+1时，我们能不能赢。
  5.     vector<bool> dp(n+1, true);
  7.     for(int idx = 4; idx <= n; ++idx) dp[idx] = !(dp[idx-1] && dp[idx-2] && dp[idx-3]);
  9.     return dp[n];
  10. }