常见的旋转、缩放、正交投影、镜像等变换效果就是线性变换。

一、旋转

变换物体和变换坐标系，其实是互反的的。比如将物体顺时针旋转20°，扩大200%，等价于将坐标缩小200%，在逆时针旋转20°。

1、2D旋转矩阵

只考虑旋转，不考虑平移，绕原点旋转θ角度。一般逆时针旋转被认为是正方向，顺时针旋转是负方向。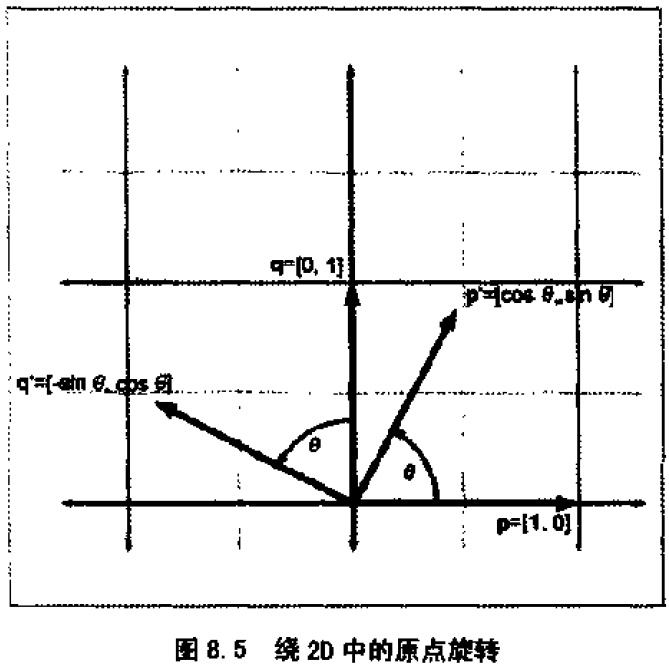

2、3D旋转矩阵

2D中是绕点旋转，3D中是绕轴旋转，轴不一定是轴，这里暂不考虑平移，只讨论旋转轴穿过原点。
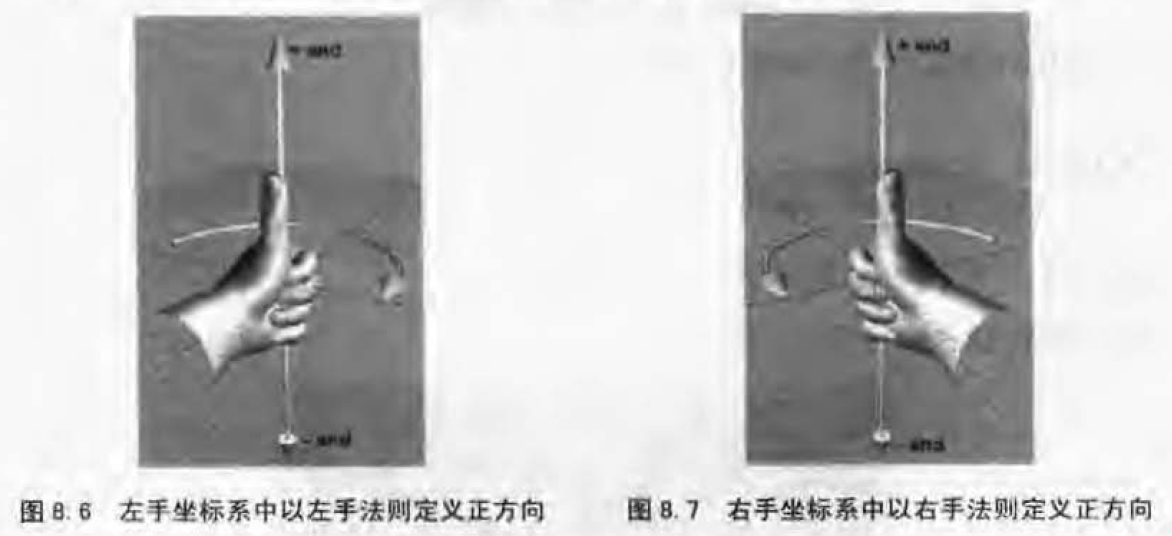
旋转的正负方向的判定规则：左手法则和右手法则。

• 左手法则
  • 左手坐标系中定义旋转方向的规则
  • 伸出左手，四指握拳，大拇指指向旋转轴的正方向，四指握拳方向就是正方向
• 右手法则
  • 右手坐标系中定义旋转方向的规则
  • 类似左手法则，左手换右手

绕x轴的旋转矩阵

绕y轴的旋转矩阵

绕z轴的旋转矩阵

绕任意轴的旋转矩阵

3D的旋转矩阵，那就需要确定3个坐标轴（基向量），这样就化简为了求绕轴旋转后的向量的问题。
问题模型如下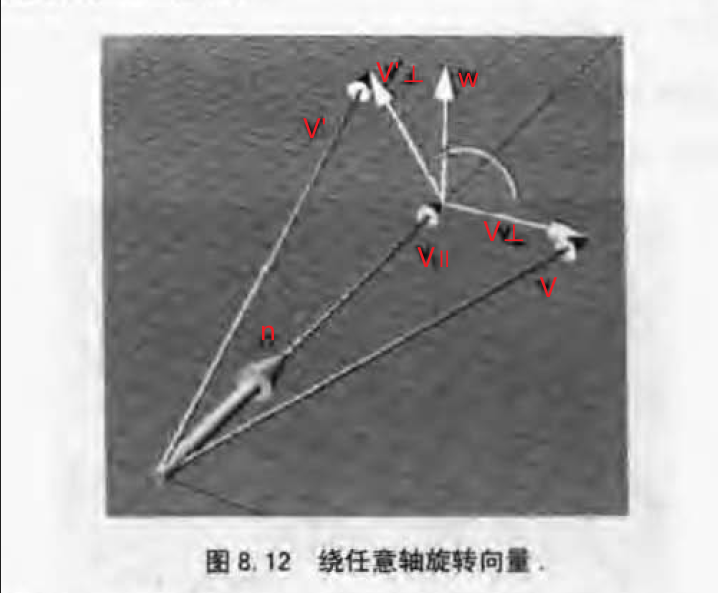

已知：

求：

根据上面学习的向量点乘投影计算：

代入公式：


获取旋转后的x轴基向量**
为了便于书写，我们以列向量的方式相乘。
。将

同上理，我们可以获得

注意，这里是用的列向量相乘，我们最终换成行向量，当然你也可以不用这么做，最终得到：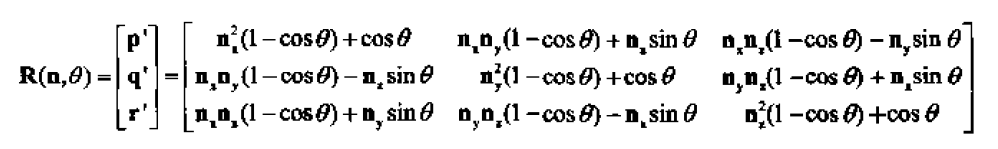

函数返回绕任意轴n旋转θ角度后得到的旋转矩阵。

二、缩放

1、沿坐标轴的缩放矩阵

最简单的缩放，沿着每个坐标轴应用单独的缩放因子


3D同理，

2、沿任意轴的缩放矩阵

和求3D旋转矩阵一样的方法，我们可以求任意向量沿n轴缩放后得到的新向量公式，问题的数学模型如下：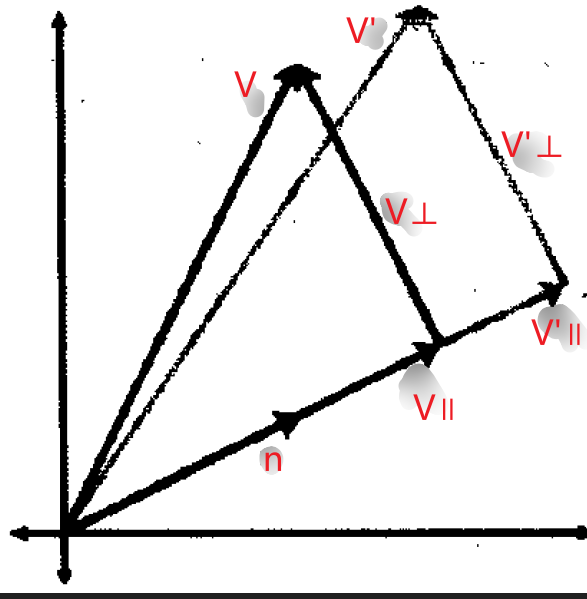

。

同理，

最终得到返回沿任意轴n缩放k倍的2D缩放矩阵的函数：

同理，返回沿任意轴n缩放k倍的3D缩放矩阵函数如下：

三、正交投影

我们先学习更简单的正交投影，后面再学习透视投影。
正交投影，也可以叫平行投影。所有点都被拉平至垂直的轴/平面，降维操作。
比如一个茶壶照在墙壁上。
有一个重要特征：不管物体位置的远近，投影的大小都等于物体实际大小。

1、向坐标轴/平面的投影

向X轴投影的2D矩阵
向y轴投影的2D矩阵
向xy平面投影的3D矩阵
向xz平面投影的3D矩阵
向yz平面投影的3D矩阵

2、向任意轴/平面的投影

咱不考虑平移，所有轴/平面必须经过原点，通过使该方向的缩放因子为0能导出该方向的投影矩阵。根据上面的缩放矩阵有：
向任意直线投影的2D矩阵

向任意平面投影的3D矩阵

四、镜像（反射）

缩放矩阵的缩放因子设置为-1即可达到镜像效果。
沿任意轴镜像的2D矩阵

沿任意平面镜像的3D矩阵

五、切变

非均匀拉伸（扭曲变化），面积和体积不发生变化。基本思想是一个坐标x因子+加到另一个坐标上。
如，得到如下图切变：

x坐标根据y坐标切变：

y坐标根据x坐标切变：
x、y坐标根据z坐标切变：

y、z坐标根据x坐标切变：

x、z坐标根据y坐标切变

六、变换组合

世界中有一个任意方向、任意位置的物体，我们要把它渲染到任意方向、任意位置的摄像机中，必须将物体顶点从物体坐标系变换到世界坐标系再变换到摄像机坐标系。其数学变换总结如下：

物体有很多顶点，变换计算需要循环很多次，但是矩阵变换都是相同的，因为变换效果都是相同的，所以我们可以将矩阵变换的乘法提出到循环外进行计算，这样可以省去大量的矩阵计算。