训练题：矩阵路径

题目：http://t.cn/A62ObxiQ

  • 时间复杂度：O(3kMN)，k为字符串长度
  • 空间复杂度：O(k) ```cpp

bool exist( vector> &board, string word ) { const auto countRow = board.size(); const auto countCol = board[0].size(); const auto wordSize = word.size(); for( int i = 0; i < countRow; ++i ) { for( int j = 0; j < countCol; ++j ) { if( dfs( board, word, countRow, countCol, wordSize, 0, i, j ) ) { return true; } } } return false; }

bool dfs( vector> &board, const string &word, const int &countRow, const int &countCol, const int &wordSize, const int &start, int i, int j ) { if( start == wordSize ) { return true; } if( i == countRow || i < 0 ) { return false; } if( j == countCol || j < 0 ) { return false; } if( board[i][j] != word[start] || board[i][j] == ‘*’ ) { return false; }

  1. char shit = board[i][j];
  2. board[i][j] = '*';
  3. if( dfs( board, word, countRow, countCol, wordSize, start + 1, i + 1, j ) ) { return true; }
  4. if( dfs( board, word, countRow, countCol, wordSize, start + 1, i - 1, j ) ) { return true; }
  5. if( dfs( board, word, countRow, countCol, wordSize, start + 1, i, j + 1 ) ) { return true; }
  6. if( dfs( board, word, countRow, countCol, wordSize, start + 1, i, j - 1 ) ) { return true; }
  7. board[i][j] = shit;
  8. return false;

}

  1. <a name="pMpfj"></a>
  2. # 训练题：顺时针打印矩阵
  3. 题目：[http://t.cn/A6GkjcYi](http://t.cn/A6GkjcYi)
  4. <a name="caKLL"></a>
  5. ## 方法一：模拟法
  7.    - 时间复杂度：O(m*n)
  8.    - 空间复杂度：O(m*n)
  10. 模拟法，模拟顺时针的过程，递归模拟。
  11. ```cpp
  13. vector<int> spiralOrder( vector<vector<int>> &matrix )
  14. {
  15.     if( matrix.empty() ) { return {}; }
  17.     const auto countRow = matrix.size();
  18.     const auto countCol = matrix[0].size();
  20.     // 0：水平往右遍历
  21.     // 1：垂直往下遍历
  22.     // 2：水平往左遍历
  23.     // 3：垂直往上遍历
  24.     char direction      = 0;
  26.     vector<int> ret;
  27.     ret.reserve( countRow * countCol );
  29.     // 保存已经遍历的元素
  30.     vector<vector<bool>> visited( countRow, vector<bool>( countCol, false ) );
  32.     _print( matrix, visited, ret, countRow, countCol, direction, 0, 0 );
  33.     return ret;
  34. }
  36. bool _print( vector<vector<int>> &matrix, vector<vector<bool>> &visited, vector<int> &container, const int &countRow, const int &countCol, char &direction, int i, int j )
  37. {
  38.     // 索引已经越界或者已经被访问过了
  39.     if( j >= countCol || j < 0 || i >= countRow || i < 0 || visited[i][j] ) { return false; }
  41.     // 记录访问元素
  42.     container.push_back( matrix[i][j] );
  43.     visited[i][j] = true;
  45.     // 先尝试继续相同方向的访问，如果失败了就切换到下一个方向尝试。
  46.     if( direction % 4 == 0 && !_print( matrix, visited, container, countRow, countCol, direction, i, j + 1 ) ) { ++direction %= 4; }
  47.     if( direction % 4 == 1 && !_print( matrix, visited, container, countRow, countCol, direction, i + 1, j ) ) { ++direction %= 4; }
  48.     if( direction % 4 == 2 && !_print( matrix, visited, container, countRow, countCol, direction, i, j - 1 ) ) { ++direction %= 4; }
  49.     if( direction % 4 == 3 && !_print( matrix, visited, container, countRow, countCol, direction, i - 1, j ) ) { ++direction %= 4; }
  50.     if( direction % 4 == 0 && !_print( matrix, visited, container, countRow, countCol, direction, i, j + 1 ) ) { ++direction %= 4; }
  52.     return true;
  53. }

方法二：层遍历

  • 时间复杂度：O(m*n)
  • 空间复杂度：O(1)

从外层往内层遍历，依次打印每层的上、右、下、左。

  2. vector<int> spiralOrder( vector<vector<int>> &matrix )
  3. {
  4.     if( matrix.empty() ) { return {}; }
  6.     const auto countRow = matrix.size();
  7.     const auto countCol = matrix[0].size();
  9.     // 记录当前的层索引
  10.     char left   = 0;                
  11.     char right  = countCol - 1;        
  12.     char top    = 0;
  13.     char bottom = countRow - 1;
  15.     vector<int> ret;
  16.     ret.reserve( countRow * countCol );
  18.     while( true )
  19.     {
  20.         for( int tmp = left; tmp <= right; ++tmp ) { ret.push_back( matrix[top][tmp] ); }
  21.         if( ++top > bottom ) { break; }
  23.         for( int tmp = top; tmp <= bottom; ++tmp ) { ret.push_back( matrix[tmp][right] ); }
  24.         if( --right < left ) { break; }
  27.         for( int tmp = right; tmp >= left; --tmp ) { ret.push_back( matrix[bottom][tmp] ); }
  28.         if( --bottom < top ) { break; }
  30.         for( int tmp = bottom; tmp >= top; --tmp ) { ret.push_back( matrix[tmp][left] ); }
  31.         if( ++left > right ) { break; }
  32.     }
  34.     return ret;
  35. }

训练题：旋转矩阵

题目：http://t.cn/A6Zekoeu

方法一

  • nums[i][j]，旋转之后，到了nums[j][n - i - 1]的位置。

  • 用一个相同大小的辅助数组保存旋转后的矩阵

  • 时间复杂度：O（N）

  • 空间复杂度：O（N）

    方法二：模拟旋转

  • 时间复杂度：O（N）

  • 空间复杂度：O（1）

以nums[0][0]元素为例，旋转后到了右上角，这时如果我们再将右上角这个被覆盖之前的元素再旋转到右下角，以此类推，总共旋转4次，最后又旋转到了nums[0][0]，这时我们就完成了四个角元素的旋转。我们称这个为一个循环循环。
以下图描述了n分别为奇数和偶数时，我们可以对这4个部分的每个元素进行一个旋转循环就完成了整个矩阵的旋转。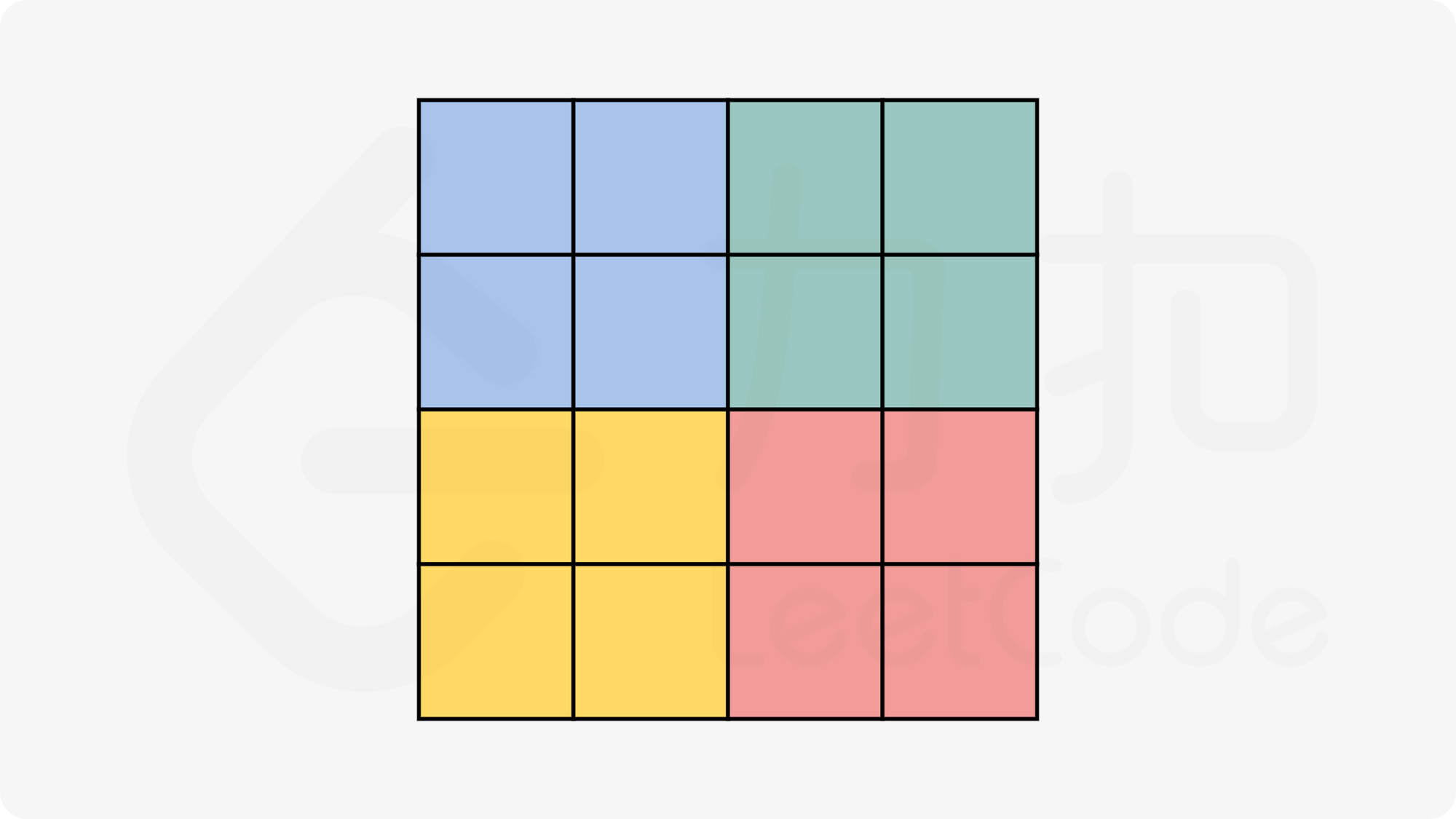
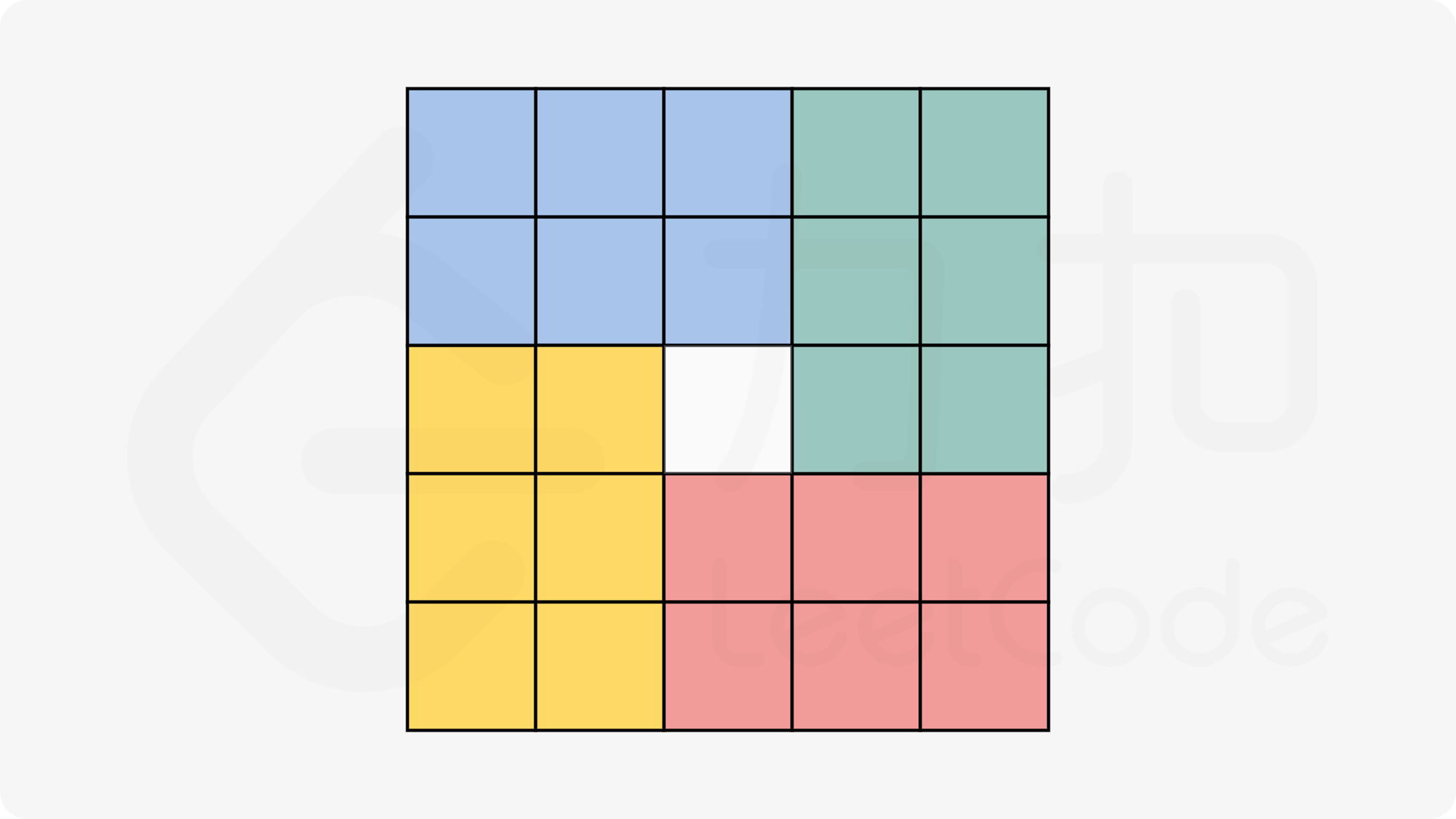
算法训练_矩阵、图 - 图1算法训练_矩阵、图 - 图2

  2. void rotate(vector<vector<int>>& matrix) {
  3.     if(matrix.size() < 2) return;
  5.     const auto size = matrix.size();
  7.     int startI = 0, startJ = 0, nextVal = 0, tmp;
  8.     int row = 0, col = 0;
  10.     if(size & 0x1){
  11.         row = (size - 1) >> 1;
  12.         col = (size + 1) >> 1;
  13.     }
  14.     else row = col = size >> 1;
  16.     for(int i = 0; i < row; ++i){
  17.         for(int j = 0; j < col; ++j){
  19.             // 一个旋转循环
  21.             startI = i, startJ = j;
  22.             nextVal = matrix[i][j];
  23.             while(true) {
  24.                 tmp    = startI;
  25.                 startI = startJ;
  26.                 startJ = size - tmp - 1;
  28.                 tmp = matrix[startI][startJ];
  29.                 matrix[startI][startJ] = nextVal;
  30.                 nextVal = tmp;
  31.                 if(startI == i && startJ == j) break;
  32.             }
  33.         }
  34.     }
  35. }

方法二：翻转代替旋转

  • 时间复杂度：O（N）
  • 空间复杂度：O（1）

旋转90° = 上下翻转 + 主对角线翻转。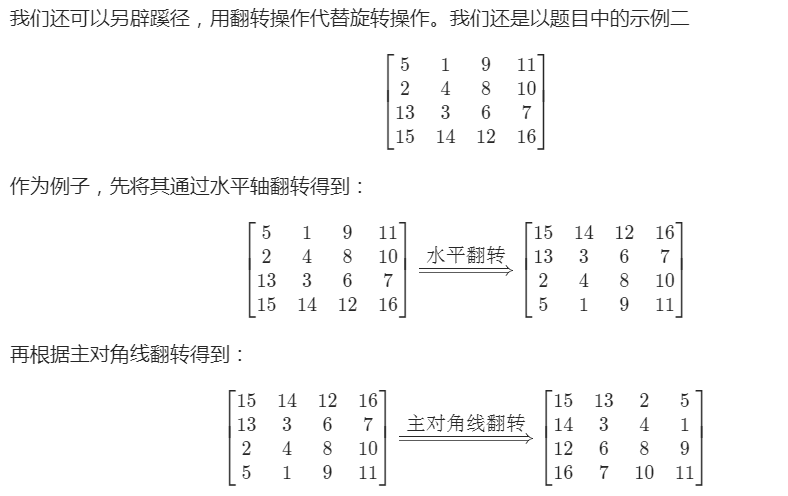
image.png

  2. void rotate(vector<vector<int>>& matrix) {
  3.     if(matrix.size() < 2) return;
  5.     const auto size = matrix.size();
  6.     const auto size_2 = (size >> 1);
  8.     // 上下翻转
  9.     for(int row = 0; row < size_2; ++row){
  10.         for(int col = 0; col < size; ++col)
  11.             std::swap(matrix[row][col],matrix[size - 1 - row][col]);
  12.     }
  14.     // 主对角线翻转一次
  15.     for(int row = 0; row < size; ++row){
  16.         for(int col = row + 1; col < size; ++col)
  17.             std::swap(matrix[row][col], matrix[col][row]);
  18.     }
  19. }

训练题：矩阵找数

题目：http://t.cn/A624BDfp

方法一：二叉搜索树

将矩阵逆时针旋转45°就是一个二叉搜索树。左节点<父节点<右节点。
我们从根节点（右上角位置）开始遍历查找，

  2. bool findNumberIn2DArray(vector<vector<int>>& matrix, int target) {
  3.     if( matrix.empty() || matrix[0].empty() ) { return false; }
  5.     const auto n = matrix.size();
  7.     for( int i = 0, j = matrix[0].size()-1; i < n && j >=0; )
  8.     {
  9.         if( matrix[i][j] > target ) { --j; }
  10.         else if( matrix[i][j] < target ) { ++i; }
  11.         else { return true; }
  12.     }
  13.     return false;
  14. }

方法二：同理

既然可以右上角，那也可以左下角。本质一样，只不过方向别扭。

  2. bool findNumberIn2DArray(vector<vector<int>>& matrix, int target) {
  3.     if( matrix.empty() || matrix[0].empty() ) { return false; }
  4.     const auto m = matrix[0].size();
  5.     for( int i = matrix.size() - 1, j = 0; i >= 0 && j < m; )
  6.     {
  7.         if( matrix[i][j] > target ) { --i; }
  8.         else if( matrix[i][j] < target ) { ++j; }
  9.         else { return true; }
  10.     }
  11.     return false;
  12. }