一、参考资料

• http://www.songho.ca/opengl/gl_projectionmatrix.html

投影（矩阵变换）是将3D转化2D的核心过程，可以把这个过程想象成这样：

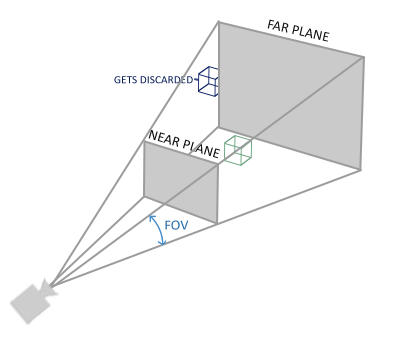
把摄像机比作人的眼睛，它决定了我们看向何处，还有看的方位，举个例子，我们躺在床上看天花板的灯，头在床头、头在床尾，还有横躺着看，在我们眼里灯好像旋转了一样。

六个面分别是：上下、左右、远近平面（Near/Far Plane）
眼睛所能看到的范围是近平面（Near Plane）、远平面（Far Plane）、上平面（Top Plane）、下平面（Bottom Plane）、左平面（Left Plane）、右平面（Right Plane）包围的的空间，叫做视景体（View Volume）、视体（viewing frustum）、平截头体（Frustum）、或者视锥。在视景体范围之外的物体，我们是看不到的（视野有限，被裁剪掉）。

物体成像在近平面（NearPlane）上，物体模型的顶点和眼睛的连线相交于近平面上的一点，该点就是顶点在我们眼睛里的成像。

有两种投影变换效果，正交投影（Ortho Projection）和透视投影（Perspective Projection）。这两种变换用于不同的场景。

二、正交投影（Ortho Projection）

也叫正射投影，Orthographic Projection Matrix。
正交投影的视景体是长方体形状。物体模型的顶点是以垂直于近平面的方向，投影到近平面。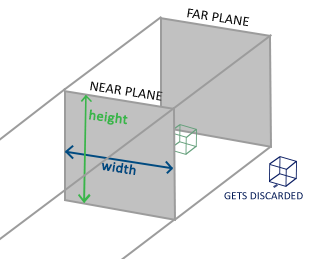

最终的投影效果是：不管物体位置的远近，物体的投影（成像）大小都是物体的实际大小，这会造成很不真实的感觉。比如你看很远和很近的人都是一样大。适用于一些没有远近概念的场景，要表现物体真实大小的场景，比如：

• 2D游戏
• 几何图形展示

  三、透视投影（Perspective Projection）

  透视投影的视景体，我们一般叫做平截头体，就像一个削了顶的金字塔形状。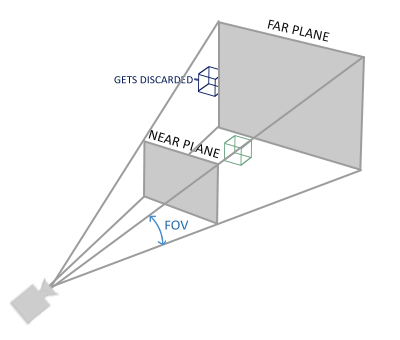
  
  FOV（Filed of View），视野，在投影矩阵构建函数中的参数，一般设置为，可以达到比较真实的效果。
  投影效果最显著的特征就是近大远小（远的物体，在x、y、z方向上都会被一定程度的压缩），叫做透视缩略，符合人类的视觉模型。
  一般用于3D模拟。
  

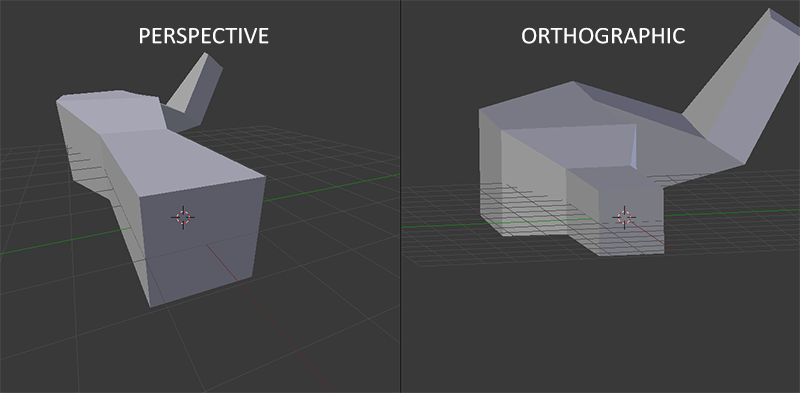
下图展示了正交投影和透视投影的投影效果。

四、求解投影矩阵

（一）透视投影矩阵

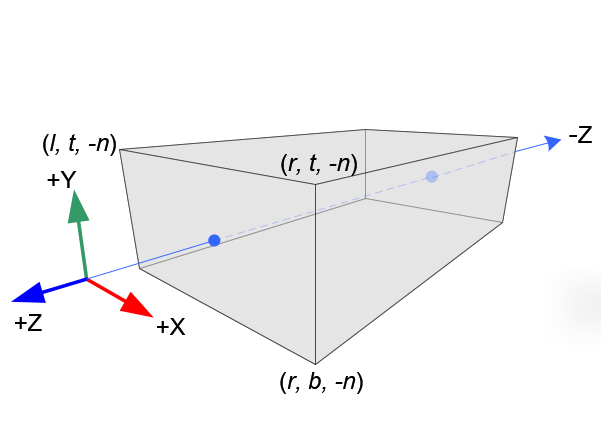
坐标系为观察（视图）坐标系，摄像机位置在坐标系原点，摄像机朝向-Z轴方向。
视景体是一个平截头体（削了顶的金字塔）。
。
。
近平面方程：
远平面方程：

设观察空间（View Space）的某点坐标为，这是投影矩阵上一步的视图变换输出的坐标，投影到近平面上的投影坐标为。
下面两图分别是视景体俯视/侧视图：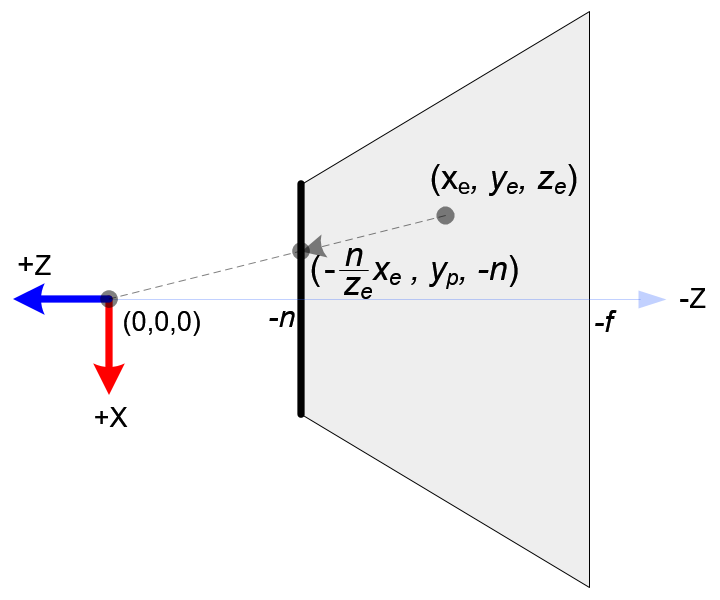

根据相似三角形关系有：

为了让投影坐标可以灵活映射到指定大小的显示区域（视口，ViewPort）上，科学家们想到一个很好的办法，在中间加入一个适配环节（归一化），就是说提出一个标准设备坐标（NDC，Normal Device Coordinates）的概念，将显示区域的坐标设定在的范围，即显示区域的左下角坐标为，右上角坐标为。用数学来表达就是：
，有，其中为线性函数，且有：


我们可以求出如下：

代入等式1、2，有：

设裁剪坐标（先别管为啥叫裁剪），投影矩阵，

令（等式4.5），我们现在要从结果逆一步步推出矩阵的结构，这个裁剪坐标就是投影变换后的结果，然后我们需要再将裁剪坐标转换成坐标，我们从等式3、4的结果中令

则有

我们可以用齐次坐标的第四个分量来保存一个数据，令，有：

我们可以逆向推出矩阵的一部分：

仔细查看等式5、6，结合矩阵与向量乘法特性，我们又可以逆推出矩阵的一部分：

我们还需要解出矩阵的第三行，我们可以填充假设变量，如下：

根据矩阵与向量乘法规则，有：

我们可以知道，对于视景体内任意点，它的x、y坐标的值不应该影响到投影后坐标的z值，所以，有：

然后有

根据等式7、8，为了保持计算的统一，显然我们很容易联想到：，将等式12代入，有：

我们知道，，且有：

时，。
时，。

分别代入等式13，同时我们可以令有：

解二元一次方程，我们可以得到：，，代入等式13得到：


同上面等式9的逆推技巧，我们可以令，则有：

，我们可以逆推出矩阵的元素：

至此，我们已经推算出针对一般情况的投影矩阵：

。
。
近平面方程：
远平面方程：

设，NDC坐标，
观察空间（View Space）任意某点坐标的齐次坐标，
裁剪坐标的齐次坐标，有：

，

假如视景体的坐标是对称的，即，投影矩阵可简化为：

深度值函数

我们知道NDC坐标的z坐标值其实就是后续深度测试（Depth Test）要用到的深度值（Depth）
回到上面的等式14，我们有：

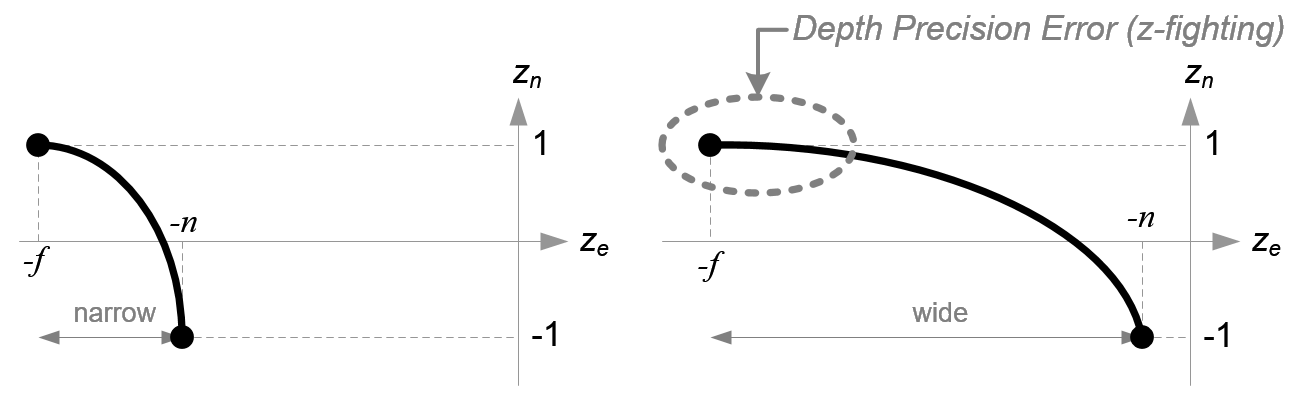
我们可以看到观察空间的点的z坐标和深度值depth之间并不是线性函数，根据该函数的曲线分布特性我们知道，当ze越靠近近平面，深度值有更好的精度，而越靠近远平面，精度越低。如果远近平面的距离越大，即的范围越大，在靠近远平面的地方越容易发生Z冲突（Z-fighting，在靠近远平面的点投影变换后得到的深度值的差异非常小，如果数据值超过了支持的精度，则会认为这两个深度值相等）。我们应该尽可能地的缩小的范围，如下图解释：

（二）正交投影矩阵

坐标系为观察（视图）坐标系，摄像机位置在坐标系原点，摄像机朝向-Z轴方向。
视景体为一个长方体。
。
。
近平面方程：
远平面方程：

视景体内的点是垂直投影到近平面上，因此我们有：
，很显然z坐标也应该是线性映射关系，我们可以令。

同上透视投影矩阵求解过程中关于投影坐标与NDC坐标之间的映射关系，我们有：

，有如下关系：

其中为线性函数，且有：

我们可以求出如下：

将投影坐标替换成被投影的点的坐标（观察坐标），有

同上面等式9的推理，我们可以推出裁剪坐标、正交投影矩阵、观察坐标之间的关系：

其中。

同样的，如果视景体的坐标是对称的，即，则正交投影矩阵结构如下：