- 数学定义
- 一个向量是一个数组(数字列表)。
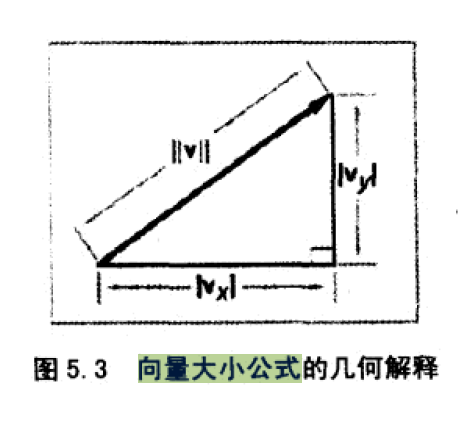
- 几何定义
- 一个向量是一个有大小和方向的有向线段。
- 大小
- 向量的长度(模),非负 。
- 维度
- 向量包含的“数”的数目。
标量,是对数值的技术称谓,强调的是数值。
位移、速度是向量,长度和速率是标量。
一、表示形式
1、数学形式
一般用x、y、z、w来分别表示2D、3D、4D向量的第1、2、3、4个分量的下标。**
2、几何形式
二、零向量
每一维都是0,大小为0,没有方向。
三、负向量
1、几何意义
对一个向量取负的几何意义是得到一个大小相等,反向相反的向量。
四、向量大小
各分量平方和的平方根。
2、几何意义
五、标准化向量
大小为1的向量,也叫单位向量、法线。只关注方向,不关注大小。
3、几何意义
2D环境中,如果以原点为尾画一个单位向量,那么向量的头将接触到圆心在原点的单位圆,3D环境中,将接触到圆心在原点的单位球。
六、向量运算
线性代数是专门研究向量的数学分支,关注的是向量的数学意义。
3D数学关注向量的几何意义。
如线性代数只讲向量和矩阵的乘法运算步骤,却不会讲向量乘以矩阵可以实现坐标空间变换。
0、向量+标量
数学上没有定义向量与标量的加减运算,但是很多数学库为了方便,在代码上支持这样的操作。
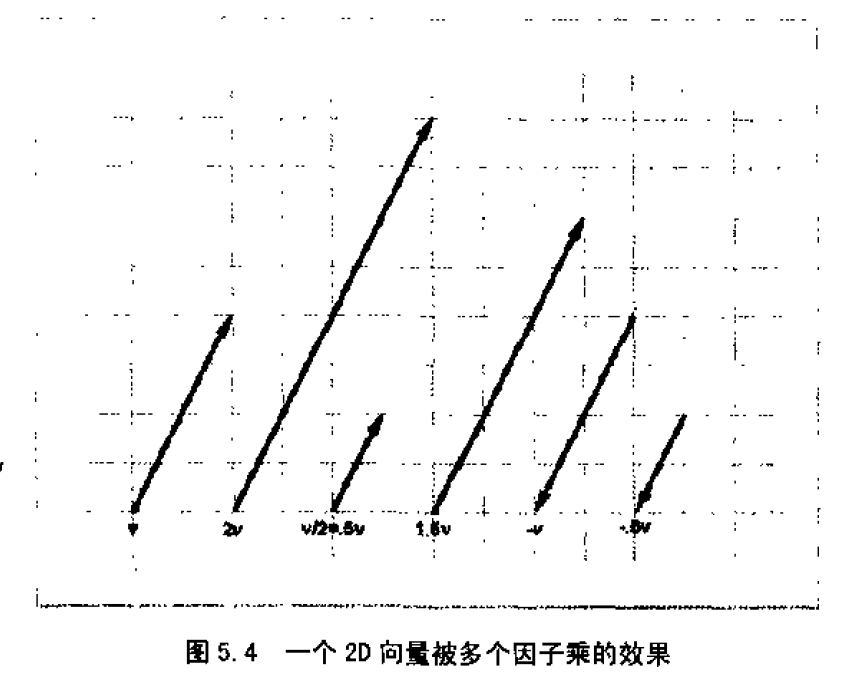
1、标量 x 向量
标量不能与向量相加,但是能相乘,乘的顺序不重要,乘号可以省略。
注意
- 标量与向量相乘,不需要写乘号。
- 标量不能除以向量,向量不能除以向量
- 负向量就是
几何意义
2、向量 ± 向量
向量的维度相同,可以相加减。
减法解释为加负向量。
注意
- 不同维度不能相加减。
- 向量加法满足交换律,减法不能。
几何意义
“三角形法则”。从下图可以看出,加法符合交换律,减法不符合。
点击查看【processon】
点击查看【processon】
根据三角形法则,向量可以被解释为与轴平行的位移序列。如矩阵,在数学上的解释为:
,在几何上的解释:向右1个单位,再向下3个单位,再向前4个单位。
七、距离公式
两点间的距离等于其中一个点到另外一个点的向量的长度。则求a、b两点间距离的过程如下:八、向量点乘
乘法符号用号,不可省略。得到的结果是一个标量。
1、几何意义:判断相似度
向量点乘的结果描述了两个向量的“相似”程度,结果越大,两向量越接近。向量接近就是大小和方向的接近。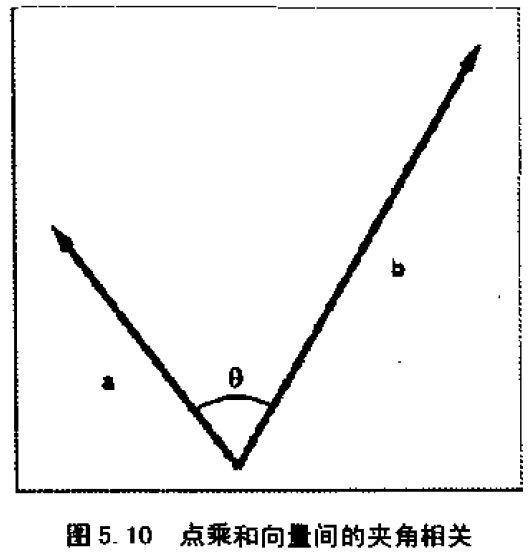
**
2、几何意义:判断夹角类型
| a · b(向量点乘) | 夹角θ类型 | 几何意义 |
|---|---|---|
| > 0 | 锐角 | a、b向量,方向基本相同 |
| = 0 | 直角 | a、b向量正交 |
| < 0 | 钝角 | a、b向量,方向基本相反 |
从上表可知,正交时,点乘为零,而零向量与所有向量相乘=0,所以零向量与所有向量正交。
实际应用场景:一个向量与平面的法向量平行,这是还需要确定向量与法向量是否同向。**
3、几何意义:向量投影

九、向量叉乘
乘法符号用表示,不能省略,也叫叉积,仅可用于3D向量。
点乘得到标量,叉乘得到向量且不满足交换律。
向量和标量之间没有叉乘。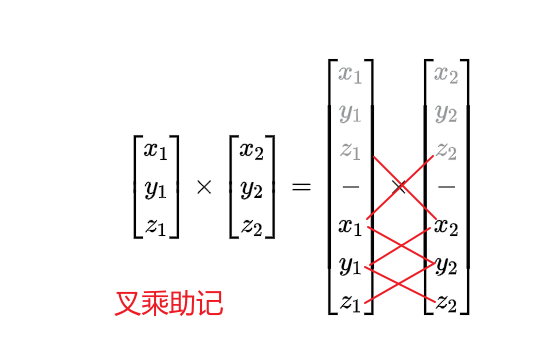
1、优先级
乘法在加减法之前,叉乘先于点乘。称作三重积。
,不满足交换律。
,满足反交换律
,不满足结合律
2、几何意义:得到垂直向量
3、几何意义:叉乘大小=面积
叉乘得到的向量的大小,等于a、b为边的平行四边形的面积。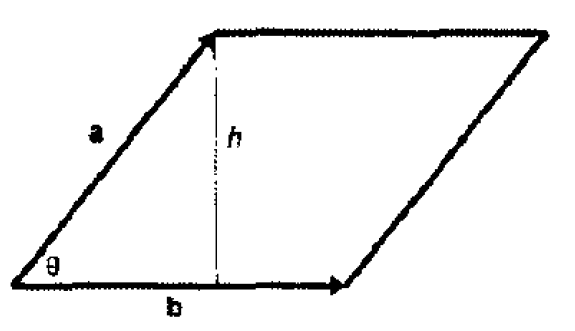
叉乘认为,零向量平行于任意向量。
**
4、几何意义:法向量是否指向你
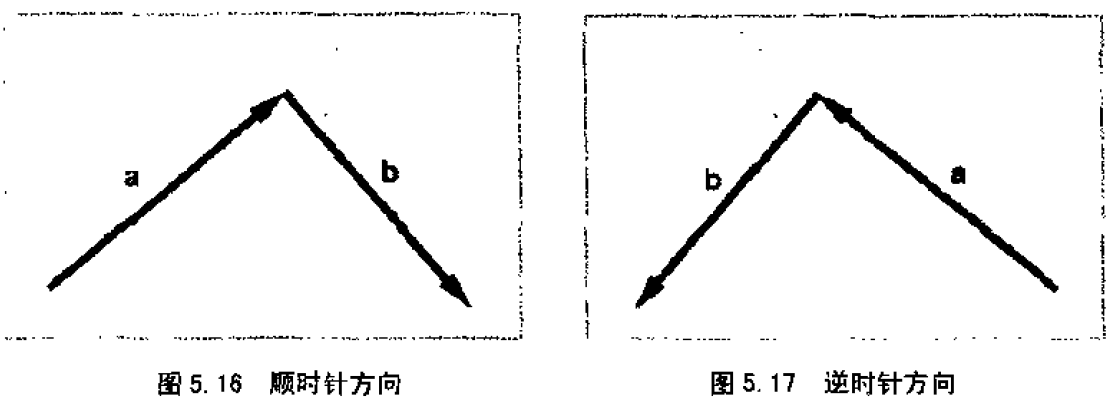
在左手坐标系中,a、b呈顺时针方向,向量指向你,反之远离你。
在右手坐标系中,a、b呈逆时针方向,向量指向你,反之指向你。
**
5、实践应用
十、向量数学公式
加粗的是向量,普通的是标量,只存在向量时,向量不加粗。
,向量乘以标量,标量相当于缩放因子。
,向量大小非负
,向量加法的三角形法则