一、检索

有n组记录：(k, I)，(k, I)，……，(k, I)
给定关键码K，检索就是找到记录(k, I)，是的k = K。
所以检索，就是查找定位。

1、检索已排序数组

顺序检索：挨个挨个找。
二分法检索。
字典检索/插值检索：根据被检索的关键码的分布知识，估算接下来往哪里找，比如“查字典”。

2、自组织线性表

记录的访问概率随着时间变化，自组织线性表就是为了解决这些问题。
每访问一次记录，自组织线性表就会适当地修改记录顺序，这种就叫启发式，常见的启发式规则：
1、计数法：为每个记录保存访问次数，类似“LFU”最不频繁使用法，但是这并不能体现访问概率随着时间变化，因为计数法认为访问多的以后一直也访问多。
2、移至前端法：访问了一次就排在最前面。类似LRU，最近最少使用法。
3、转置transpose：被访问一次，记录就和前一条记录交换位置。

优势是，不需要对记录进行排序，也不需要额外空间。

3、集合的检索

确定记录是否在集合中。
位向量bit vector、位图bitmap：有bit来表示是否存在。

集合A - B 等价于 A & ~B

签名文件：signature file，用一个bit vecot来表示文件文档中出现的关键字。

4、散列方法

根据关键码值，直接访问表。
散列hashing，把key映射到表的位置，来访问记录。它的函数叫散列函数hash function，h表示，存放的记录叫散列表（hash table，HT）。散列表的一个位置称为槽slot，槽数量用M表示，则散列就是：
对于任意关键码值K，有 0 <= h(K) <= M，HT[ i ] = K
使用于集合，不适用于范围搜索，最适合“如果有的话，哪条记录的关键码是K”

把记录映射到槽，越均匀越好，就是每个槽概率相同，也就是散列冲突概率最小。

散列冲突，就是h(K) == h(K)。

关键码值的分布直接影响散列函数的设计。

  1. //散列函数例子
  2. //散列效果很差，因为只考虑了x的低4bit，这样很容易导致散列冲突。
  3. //此时M = 16，所以M的大小对散列的好坏也很关键。
  4. int h(int x){
  5.     return (x % 16);
  6. }
  8. //这是个很好的字符串散列函数
  9. int h(char *x){
  10.     int i, sum;
  11.     for(sum = 0, i = 0; x[i] != '\0'; i++)
  12.         sum += (int)x[i]
  13.     return (sum % i);
  14. }
  16. //更好的字符串散列函数，ELFhash
  17. //适合任意长的字符串，效果都很好，每个字符的作用都相同。
  18. int ELFhash( char* key){
  19.     unsigned long h = 0;
  20.     while(*key){
  21.         h = (h << 4) + *key++;
  22.         unsigned long g = h & 0xF0000000L;
  23.         if(g) h ^= g >> 24;
  24.         h &= ~g;
  25.     }
  26.     return h % M;
  27. }

散列冲突解决：开散列方法

散列冲突解决：开散列方法（单链方法）和闭散列方法（开地址方法）。
开散列方法：冲突记录存储在表外。
闭散列方法：冲突记录存储在表内另一个槽。

每个槽定义为链表表头，每个槽存储一条记录和一个指向链表其余部分的指针。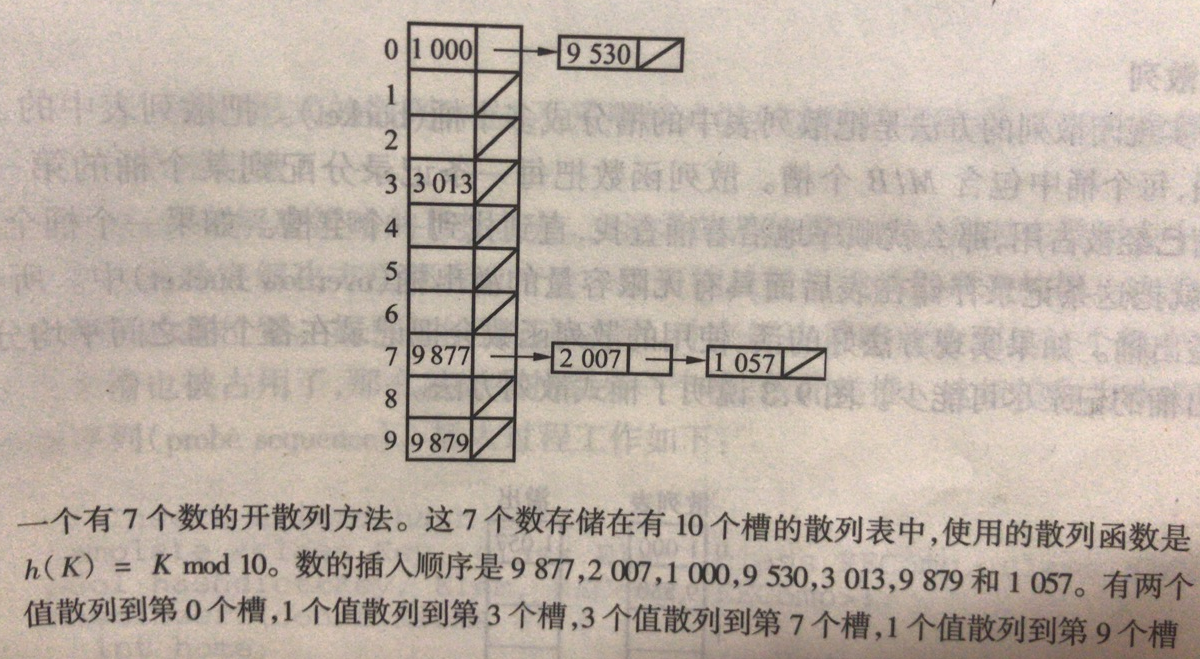
image.png
散列表放在主存中，链表也在主存中，用开散列方法最合适。如果是在磁盘，会有多次I/O，抵消了散列优势。

散列冲突解决：闭散列方法

桶式散列：“物理数组”

M个槽，分到B个桶里。还有一个溢出桶，无限容量。先往桶里插，满了都插入到溢出桶。
image.png
改进：把关键码散列到基位置，就像没有桶一样，然后在所在桶遍历，是否有空槽。如一条记录散列到slot 5，桶大小为8，第一个桶包含0~7个槽，则冲突解决过程就是：5、6、7、0、1、2、3、4。
非常适合磁盘散列，把桶设置为block大小，桶满了才进行IO操作。

线性探查：“逻辑数组”

冲突解决的过程就是在找下一个槽，可以想象成有一个“逻辑数组”包含所有的槽，这个数组的首位置是散列的基位置home，下一个位置是home+offset，而offset = p(k，i)，k是关键码值，i是这个逻辑数组的第几个槽。如home的下一个位置就是home + p(k, 1)。
上面的这个函数就叫probe function探查函数。简单的探查函数可以是：
p(K, i) = i
home：基位置（散列值）
pos：可以插入的槽位置
K：关键值码
i：偏移home的第 i 个槽
p(K, i)：探查函数
M：槽数量
散列值为home的记录K的插槽位置是：
pos = (home + p(K, i)) % M
从这个等式我们知道，探查函数是根本。

  1. template<class Key, class Elem, class KEComp, class EEComp>
  2. bool hashInsert(const Elem& e){
  3.     int home;
  4.     int pos = home = h(getkey(e));
  6.     //找到“逻辑数组”的第一个空位置
  7.     for(int i = 1; !(EEComp::eq(EMPTY, HT[pos])); i++){        
  8.         pos = (home + p(getkey(e), i)) % M;            //pos位置不空，就找下一个位置。
  9.         if(EEComp::eq(e, HT[pos])) return false;    //记录相同冲突，就不插入了。
  10.     }
  11.     HT[pos] = e;    // 找到了第一个空位置。
  12.     return true;
  13. }
  15. //hash查找是否有K的记录，
  16. //按照上面线性探查的理解，就是从头遍历“逻辑数组”查找，找到返回记录的值。
  17. bool hashsearch(const Key& K, Elem& e) const{
  18.     int home;
  19.     int pos = home = h(K);
  20.     for(int i = 1; !KEComp::eq(K, HT[pos]) && !EEComp::eq(EMPTY, HT[pos]); i++)
  21.         pos = (home + p(K, i)) % M;
  22.     if(KEComp::eq(K, HT[pos])){
  23.         e = HT[pos];
  24.         return true;
  25.     }
  26.     return false;
  27. }

线性探查散列不均匀问题

可能散列不均匀！，每个槽的散列概率不均匀。这个问题叫基本聚集primary clustering。如下图：
探查函数p(K, i) = i。
造成问题的本质原因是因为两个不同的K，探查序列相同，就和散列相同是相类似的效果，应该要让不同的K，产生的探查序列也不同。更术语的话就是探查函数p的变量太少。改进的过程其实就是改进探查函数的过程。
image.png
方法一：伪随机探查
p(K, i) = Perm[i - 1]
Perm是一个数组，长度M - 1，保存的是1~M-1数的随机排列。
方法二：二次探查
p(K, i) = i
方法一二还是有问题，因为没有引入K变量，导致如果K相同，home起点就相同，探查序列就完全相同。
方法三：双散列法
p(K, i) = i * h(K)

字典ADT（散列表实现）

  1. template<class Key, class Elem, class KEComp, class EEComp>
  2. class hashdict : public Dictionary<Key, Elem, KEComp, EEComp>{
  3. private:
  4.     Elem* HT;        //哈希表HT（数组）
  5.     int M;            //slot的总数量，HT的size
  6.     int currcnt;    //HT当前的元素数量
  7.     Elem EMPTY;        //用户自定义一个空值。
  8.     int p(Key k, int i) const { return i };        //线性探查的探查函数
  9.     int h(int x) const { return x % M };        //整形的散列函数
  10.     int h(char* x) const;                        //字符串的散列函数
  11.     bool hashInsert(const Elem&);                //哈希插入
  12.     bool hashSearch(const Key &, Elem&) const;    //哈希查找
  13. public:
  14.     hashdict(int sz, Elem e);
  15.     ~hashdict();
  16.     void clear();    //清空字典
  17.     bool insert(const Elem& e);                //插入元素
  18.     bool remove(const Key& K, Elem& e);        //删除K的元素，保存到e
  19.     bool removeAny(Elem& e);                //删除HT表中第一个非空元素
  20.     bool find(const Key& K, Elem& e) const;    //查找K值的元素
  21.     int size();        //字典当前元素数量
  23. //以下是函数实现
  24. private:
  25.     int h(char* x) const {        //前面例子中的字符串散列桉树
  26.         int i, sum;
  27.         for(sum = 0;i = 0; x[i] != '\0'; i++)
  28.             sum += (int) x[i];
  29.         return (sum % M);
  30.     }
  32. public:
  33.     hashdict(int sz, Elem selfDefineEmpty){
  34.         M = sz;
  35.         EMPTY = e;
  36.         currcnt = 0;
  37.         HT = new Elem[sz];
  38.         for(int i = 0; i < M; i++) HT[i] = EMPTY;
  39.     }
  40.     ~hashdict(){ delete[] HT; }
  41.     void clear(){
  42.         for(int i = 0; i < M; i++) HT[i] = EMPTY;
  43.         currcnt = 0;
  44.     }
  45.     bool insert(const Elem& e){
  46.         if(currcnt == M) return false;
  47.         if(hashInsert(e)){
  48.             currcnt++;
  49.             return true;
  50.         }
  51.         else return false;
  52.     }
  53.     bool remove(const Key& K, Elem& e){}
  54.     bool removeAny(Elem& e){    // 删除HT表中第一个非空元素
  55.         for(int i = 0; i < M; i++){
  56.             if(!EEComp::eq(EMPTY, HT[i])){
  57.                 e = HT[i];
  58.                 HT[i] = EMPTY;
  59.                 currcnt--;
  60.                 return true;
  61.             }
  62.         }
  63.         return false;
  64.     }
  65.     bool find(const Key& K, Elem& e) const{
  66.         return hashSearch(K, e);
  67.     }
  68.     int size(){
  69.         return currcnt;
  70.     }
  71. }

闭散列方法性能分析

插入、检索不成功的代价相同（访问次数）。
删除、检索成功的代价相同（访问次数）。
负载因子α = N / M，N是记录数，M是HT大小，反应填充程度，越大，散列冲突越可能。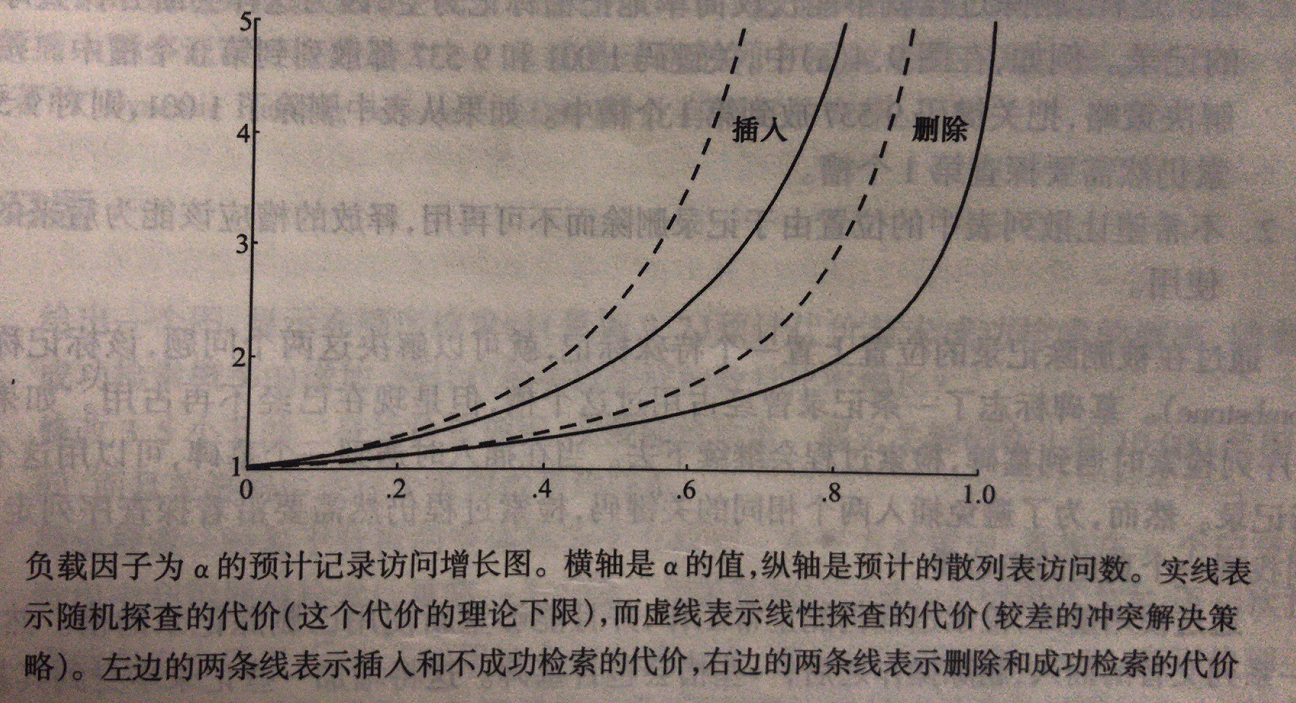
image.png
线性探查比随机探查，代价增长更快
删除和不成功检索的代价增长更快。
散列表半满之前，性能都非常好，超过之后，性能急剧下降。α=0.5最好。

改进优化

1、每当检索到记录不在基位置，就把基位置和前一条记录交换。
2、删除一条记录时，注意：
1、不能影响后续检索，就是你这里空了，不代表继续探查下去就没有了。
2、删除后槽要能继续使用。
解决办法：被删除槽置一个标记（墓碑tombstone），查找的时候检索到了，还有继续往下检索。插入的时候检索到了，可以插入记录，并取消标记。

但是随时使用次数增加，墓碑增多，探查序列也会变长，考虑解决办法：
1、删除一条记录，局部重组：后面记录交换到此槽上。
2、定时重组：把记录全部重新插入到散列表。

二、索引技术

散列擅长解决：
插入
删除
查找单个记录
散列不擅长：
范围查找（关键码值是一个范围）
输入顺序文件：按记录进入系统的顺序，把记录存储在磁盘中。
索引：indexing，把一个关键码与数据记录位置相关联的过程。
索引文件：[关键码值，记录指针]，指向记录在文件中的位置，通过指针可以直接访问到记录。
主码：primary key，记录唯一标识。
主码索引：[主码，记录指针]，指向记录在文件中的位置，通过指针可以直接访问到记录。
辅码：secondary key，不能唯一标识，不同记录辅码可能相同。
辅码索引：[辅码，主码]，如[工资，ID]。

1、线性索引

索引文件内容是：【关键码值，指针】线性存储，指针可能是指向记录位置（即可以直接访问记录），也可能是指向主码位置（在主码索引文件中的位置）。
索引是单一的一个文件，不便于数据更新。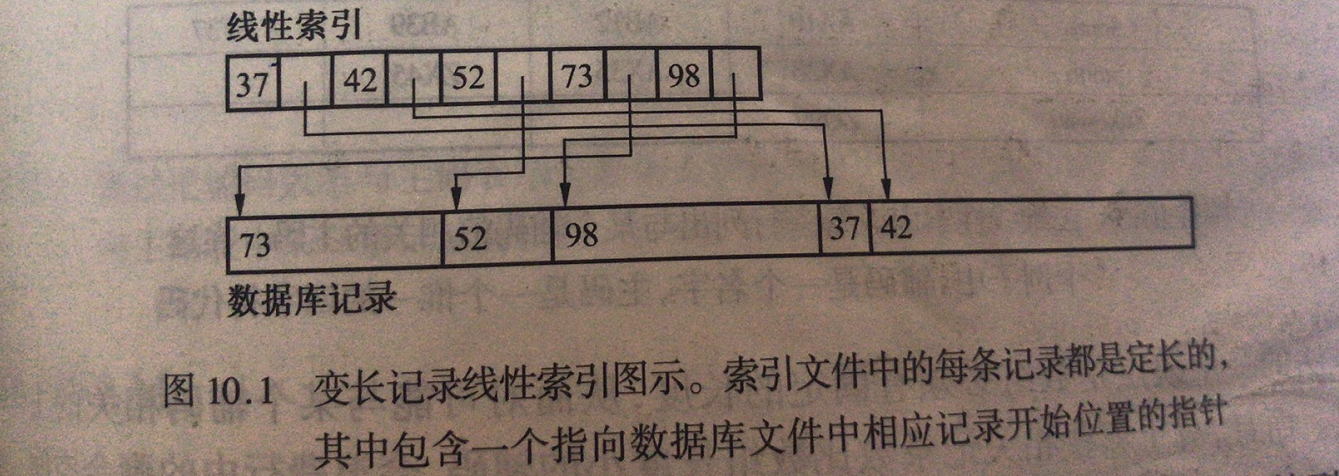
image.png
问题：记录太多，索引文件也会很大。

1.1 二级索引

记录太多，索引文件也很大，就针对索引文件再来个索引，索引文件在磁盘中，二级索引在主存中。二级索引文件内容可以是：[每次磁盘块的首个关键码值]，这样可以直接读取这个索引文件块到主存中。
image.png
缺点：
插入删除记录，因为是数组，很多索引记录要移动。
相同辅码值的多条不同记录，对应也有相同多个索引记录，辅码字段占空间。

1.2 二维线性索引

image.png
缺点：辅码相关联的主码可能没那么多，造成主码字段空间的浪费。

1.3 倒排表

image.png

2、ISAM（线性索引改进）

把索引文件分割成多个文件。
image.png
针对有限次插入删除，很有效。
问题：时间就了，系统溢出区数据增多，检索变慢。
解决：定期重新索引。

3、树形索引

十二、线性表和数组高级技术
十三、高级树结构
十四、分析技术
十六、计算限制