算法实践：https://github.com/JackieLong/algorithms/tree/main/algorithms/algorithms/inner_sort

一、概述

常见内排序算法如下：

排序算法	时间复杂度		复杂度（空间）	排序方式	稳定性
	平均	最坏
冒泡排序	O(n)	O(n)	O(1)	原地	稳定
选择排序	O(n)	O(n)	O(1)	原地	不稳定
插入排序	O(n)	O(n)	O(1)	原地	稳定
Shell排序	O(n*logn)	O(n)差不多	O(1)	原地	不稳定
归并排序	O(n*logn)	O(n*logn)	O(n)	非原地	稳定
快速排序	O(n*logn)	O(n)	O(logn)	原地	不稳定
堆排序	O(n*logn)	O(nlogn)	O(1)	原地	不稳定

原地：指占用常数内存。
三种时间复杂度
- O(n)：选择、冒泡、插入
  - 大数据表现很差，插入排序相对最好，小规模数据用插入排序最好，数据规模>1000，希尔排序比O(n)排序好的多。
- O(nlogn)：快速排序、堆排序、归并排序。
- O(n)：基数排序、桶排序。

希尔排序的时间复杂度非常难分析，在O（n）到O（n）之间，普遍认为最好是O（n）。

高级一点的排序，时间复杂度低，不稳定。
低级一点的排序算法，时间复杂度高，稳定。

改进的快速排序最出色。

任何一种基于比较的算法，都需要至少O(n*log n)的时间代价。

二、算法稳定性

“相等”元素的前后位置关系不会改变，少了这部分交换操作开销，比如比较函数加入=等号则变得不稳定。
意义：排序元素是一个有多属性的复杂对象，且排序前的顺序已存在意义，如果需要在排序之后仍保持有原排序意义，则需要使用稳定排序算法，比如对一组商品排序（价格和销量），先按销量升序排序，然后再按价格升序排序，如果使用稳定排序算法，则第二次排序之后的结果是价格相同的产品仍然是销量升序排序。
排序算法的稳定性并不固定，都和具体实现有关，比如冒泡算法” 数据结构与算法_内排序 - 图1 “改成” 数据结构与算法_内排序 - 图2 “，就变成不稳定排序，不稳定排序同样可以改成稳定排序。

二、交换排序

1、插入排序

将数列看成前/后两半部分

前：已排序序列，初始是只有一个第一个数
后：待插入前半部分的原始序列。初始是除了前的剩余部分。

“插入”过程：将“后”的首位（“前”的末位的下一位），“左移”到“合适”位置。

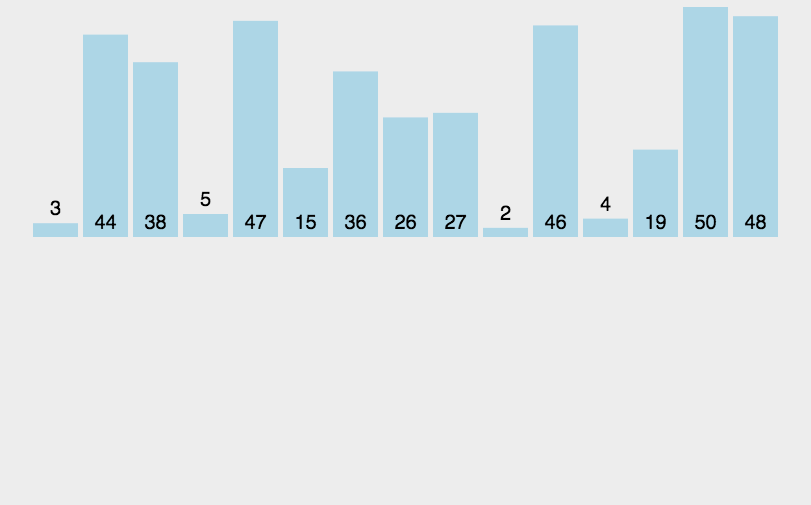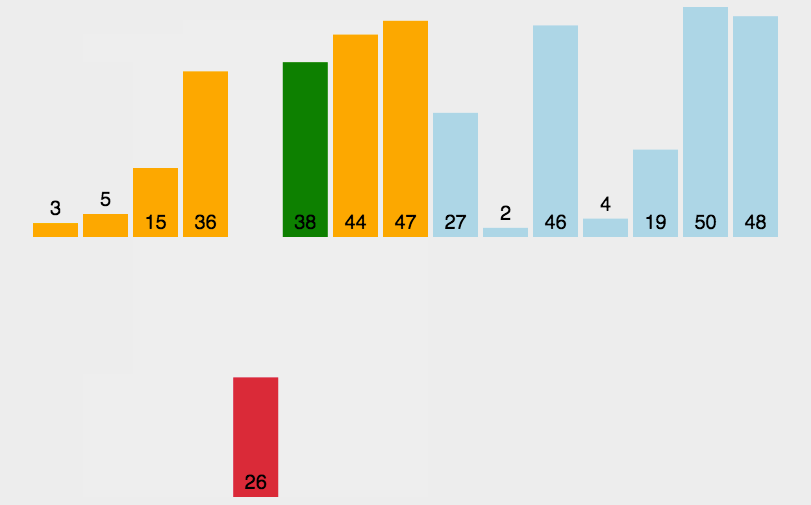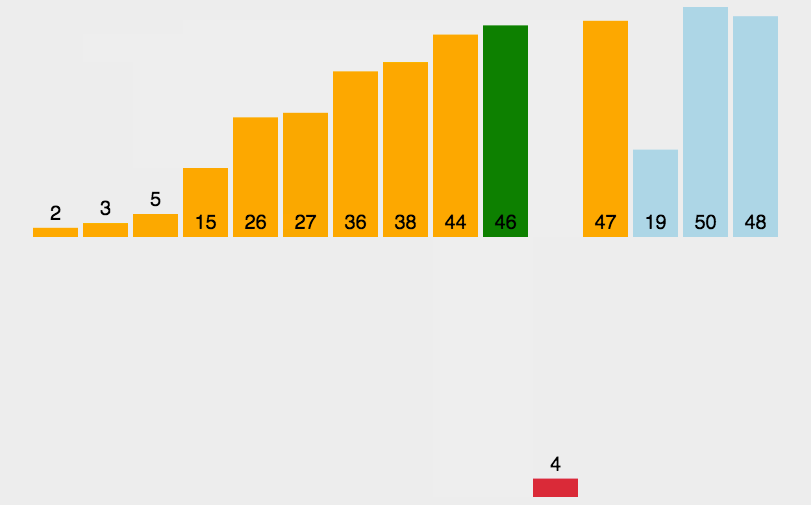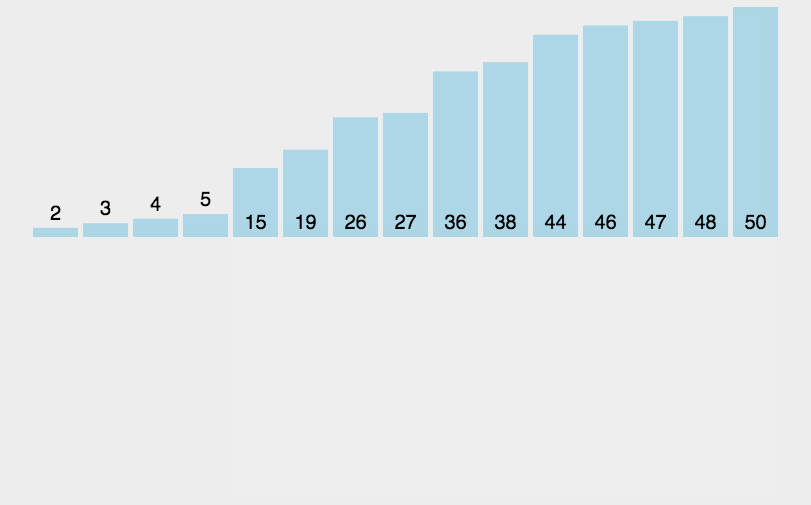
数据结构与算法_内排序 - 图3


template<class T, class Comp>
void InnerSortAlgorithm::insert_sort(T t[], int len, Comp comp) 
{
    if( len <= 1 ) { return; }
    // |------前--------| 目标  |---------后--------—|
    // t[0], ..., t[i-1], t[i], t[i+1], ..., t[len-1]
    // 每一次循环，就是将i插入前半部分中。前半部分只有1个时，其实就是有序的，因此i从1开始。
    for( int i = 1; i < len; i++ )
    {
        // j循环就是将t[i]“左移”到“合适”位置的过程。
        for( int j = i; j >= 1 && comp( t[j], t[j - 1] ); j-- )
        {
            // comp( t[j], t[j - 1] )不满足时，已经移动到了合适位置，就不需要再交换了。
            std::swap( t[j], t[j - 1] );
        }
    }
}

优化

交换太多，完全可以先找到位置，再进行交换。


vector<int> sortArray(vector<int>& nums) {
    if(nums.size() < 2) return nums;
    const auto size = static_cast<int>(nums.size());
    for(int i = 1, j, tmpNum; i < size; ++i){     
        tmpNum = nums[i];
        // 第i个元素（tmpNum）插入到[0, i-1]序列中。
        // 从i-1位置开始将所有大于i元素的元素后移一位。
        for(j = i - 1; j >= 0 && tmpNum < nums[j]; --j) nums[j+1] = nums[j];
        nums[j+1] = tmpNum;
    }
    return nums;
}

2、冒泡排序

将数列分成前/后半部分：
前：原始序列
后：已排序序列，里面的值都是数列中的最值。

冒泡过程：将“前”中的最值数，“右移”到“后”的首位的前面。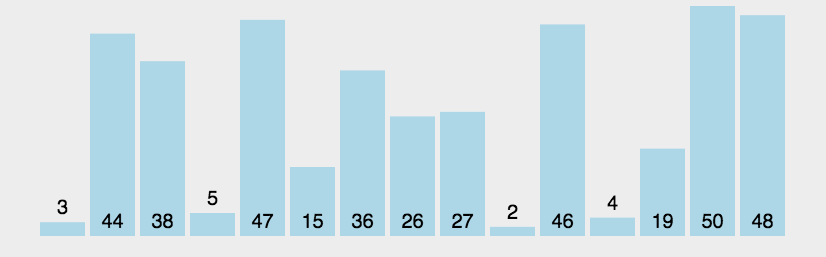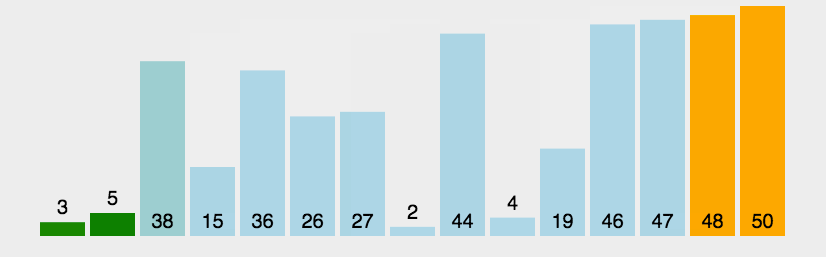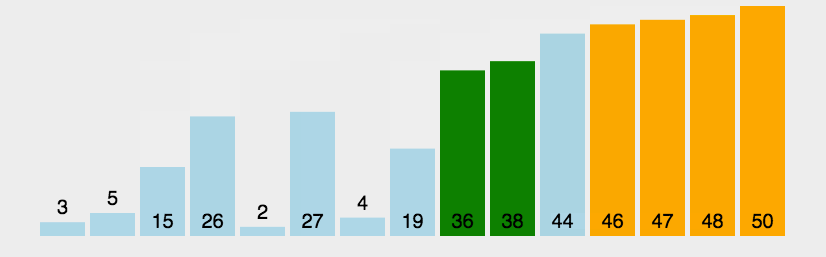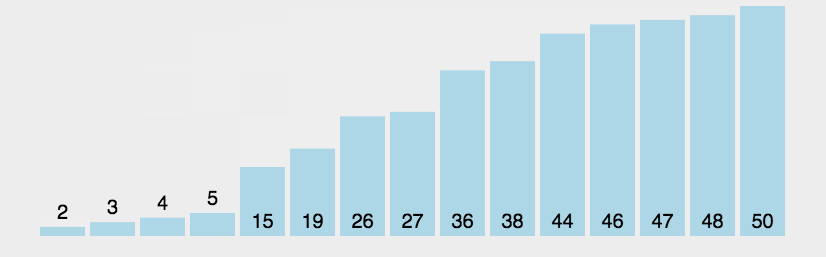


template<class T, class Comp>
void InnerSortAlgorithm::bubble_sort( T t[], const int &len, Comp comp )
{
    if( len <= 1 ) { return; }
    // |---------前---------| |----------后---------—|
    // t[0], ..., t[len-1-i], t[len-i], ..., t[len-1]
    // 一个i循环，就右移了一个最值到“后”中，只需右移len-1个，最后一个自然就是第一个。
    for( int i = 0; i < len - 1; i++ )
    {
        // 前的范围：[0, len - 1 - i]
        for( int j = 0; j < len - 1 - i; j++ )
        {
            if( !comp( t[j], t[j + 1] ) ) { std::swap( t[j], t[j + 1] ); }
        }
    }
}

优化一

如果上一轮没有发生交换，则说明序列已经有序，无需继续往下排序。


vector<int> sortArray(vector<int>& nums) {
    if(nums.size() < 2) return nums;
    const auto size = static_cast<int>(nums.size());
    // swapped表示上一轮循环是否发生交换，如果没有，则表示序列已经有序，无需再往下。
    bool swapped = true;
    for(int i = 0; i < size - 1; ++i){
        if(!swapped) break;
        swapped = false;
        for(int j = 0; j < size - 1 - i; ++j )
            if(nums[j] > nums[j+1]) {
                swap(nums[j], nums[j+1]);
                swapped = true;
            }
    }
    return nums;
}

优化二

记录最后一个交换索引，在此之后序列都是已经有序，无需判断。


vector<int> sortArray(vector<int>& nums) {
    if(nums.size() < 2) return nums;
    const auto size     = static_cast<int>(nums.size());
    bool swapped        = true;            // 中间变量，记录当前轮是否发生过交换，没有则表示整个数列已经有序。
    int swappedIdx      = -1;            // 中间变量，用于记录最后一个发生交换的索引。
    int lastUnsortedIdx = size - 1;        // 最后一个未排序的索引，也就是最后一次发生交换的第一个索引。
    while(swapped){                        // 如果上一轮没有发生交换，则表示序列已经有序
        swapped = false;
        for(int i = 0; i < lastUnsortedIdx; ++i){
            if(nums[i] > nums[i+1]){
                swap(nums[i], nums[i+1]);
                swapped = true;
                swappedIdx = i;        // 记录最后一次发生交换的第一个索引
            }
        }
        lastUnsortedIdx = swappedIdx;
    }
    return nums;
}

3、选择排序

将数列分成前/后半部分：
前：已排序序列，初始时，为空。
后：原始序列，初始时，为整个序列。

“选择”过程：将“后”中最“大”/“小”元素，放到前的末尾。
数据结构与算法_内排序 - 图5


template<class T, class Comp>
void InnerSortAlgorithm::selection_sort( T t[], const int &len, Comp comp )
{
    if( len <= 1 ) { return; }
    // 用于保存当前找到的最“大”/“小”值的索引，可以减少交换操作
    int targetIdx = -1;
    // |-------前-------| |----------后--------------|
    // t[0], ..., t[i-1], t[i], t[i+1], ..., t[len-1]
    for( int i = 0; i < len - 1; i++ )
    {
        targetIdx = i;        // t[i]
        // 找到“后”中的最值，保存到targetIdx
        for( int j = i + 1; j < len; j++ ) 
            if( !comp( t[targetIdx], t[j] ) ) { targetIdx = j; }
        // 将最值交换到t[i]，然后，t[i]归入“前”，“后”-1
        if( targetIdx != i ) { std::swap( t[i], t[targetIdx] ); }
    }
}

优化


vector<int> sortArray(vector<int>& nums) {
    if(nums.size() < 2) return nums;
    const auto size = static_cast<int>(nums.size());
    const auto size2 = size >> 1;
    // 每一轮循环都找出最大值和最小值，最大值放最后，最小值放最前，这样循环次数缩减为一半。
    for(int i = 0, idxMin, idxMax; i < size2; ++i){
        idxMin = idxMax = i;
        for(int j = i + 1; j < size - i; ++j){
            if(nums[j] < nums[idxMin]) idxMin = j;
            else if(nums[idxMax] < nums[j]) idxMax = j;
        }
        if(idxMin == idxMax) break;             // 最大值和最小值相等说明后面的元素全部相同，无需再排序。
        swap(nums[i], nums[idxMin]);            // 将最小值替换到最前面
        if(idxMax == i) idxMax = idxMin;        // 如果刚好是i，那最大值其实已经替换成idxmin那里了，要把idxMax更新到idxMin上。
        swap(nums[idxMax], nums[size-1-i]);     // 将最大值替换到最后面
    }
    return nums;
}

表现最稳定的排序算法之一，因为无论什么数据进去都是O(n2)的时间复杂度，所以用到它的时候，数据规模越小越好。唯一的好处可能就是不占用额外的内存空间了。理论上讲，选择排序可能也是平时排序一般人想到的最多的排序方法了吧。

三、希尔排序

1959年Shell发明，第一个突破O(n2)的排序算法，是插入排序的改进版。它与插入排序的不同之处在于，它会优先比较距离较远的元素，又叫缩小增量排序。
在实践中很少用到了。

算法描述

选择一个递减的增量序列：t，t，…，t，tk=1，进行k趟插入排序。
第i趟排序，将序列分割成若干元素跨度=t的子序列，分别进行插入排序。
- 第k躺排序，对整个序列进行插入排序。


// *************************************************
// 增量插入排序（插入排序的变型）
// 对下面数列进行插入排序：
// t[incr*0], t[incr*1], t[incr*2], ..., t[incr*n]
// 其中，incr*n<len 且 incr*(n+1)>=len
// *************************************************
template<class T, class Comp>
void _insert_sort( T t[], const int &len, const int &incr, Comp comp )
{
    // i=incr，相当于普通版本中的i=1，即第2个开始。
    for( int i = incr; i < len; i += incr )
    {
        for( int j = i; j >= incr && comp( t[j], t[j - incr] ); j -= incr )
        { std::swap( t[j], t[j - incr] ); }
    }
}
template<class T, class Comp>
void InnerSortAlgorithm::shell_sort( T t[], const int &len, Comp comp )
{
    // ************************************************************************************
    // 获取一系列的incr增量，最简单的做法就是/2递减，比如对100个数排序，则增量依次如下；
    // 50, 25, 12, 6, 3, 1
    // 注意，最后一个必须是1，即普通版本的插入排序，进行一次完全的排序。
    // ************************************************************************************
    std::vector<int> increments;
    increments.reserve( len >> 1 + 1 );
    for( int incr = len >> 1; incr > 0; incr = incr >> 1 )
    { increments.push_back( incr ); }
    for( auto &incr : increments )
    {
        // 假设有10个数，且incr=4，则分别以下子数列进行增量插入排序：
        // 1、t[0], t[4], t[8]
        // 2、t[1], t[5], t[9]
        // 3、t[2], t[6], t[10]
        // 4、t[3], t[7]
        for( int start = 0; start < incr; start++ )
        { _insert_sort( t + start, len - start, incr, comp ); }
    }
}

四、快速排序

BST通过根节点root把左右子树分割，且左子树<= 根 <= 右子树。如果再对左右子树这样分下去？快速借鉴了这个原理叫“分治法”divide and conquer，找一个pivot把一块数分成左右两份，左边 < pivot < 右边，pivot刚好在中间。

1、获取pivot（基准）
- 可以取序列中间的那个元素。
2、排序，使得左<=pivot<=右。
- 代码实现
  - pivot靠边：将pivot交换至末尾
  - 排序：对[0~n-2]序列，派两个人A（左）、B（右）从两头往中间进行检查，A遇到>pivot的元素就停止，B遇到<pivot的元素也停止，然后交换AB所在位置的元素，然后AB继续靠扰。
  - pivot复位：将B所在位置元素与pivot交换。
3、分别对左、右重复1、2。

数据结构与算法_内排序 - 图7


template<class T, class Comp>
void InnerSortAlgorithm::quick_sort( T t[], const int &len, Comp comp )
{
    // quick_sort_n是一个递归版本的快排
    quick_sort_n<T, Comp>( t, 0, len - 1, comp );
}
// ************************************************
// 对数组t的[start, end]闭区间的数进行快排
// ************************************************
template<class T, class Comp>
void InnerSortAlgorithm::quick_sort_n( T t[], const int &start, const int &end, Comp comp )
{
    // 0/1个数，不需要排序，直接返回。
    if( start >= end ) { return; }
    // 找到一个pivot，然后放到最尾部
    std::swap( t[findPivot( start, end )], t[end] );
    // 对数组t[start, end-1]闭区间范围的数进行partition分区，t[end]就是pivot
    // 使得left partition < pivot，right partition >= pivot。
    // 并返回first index of right partition。
    //
    // |----- < pivot----|  |--- >= pivot ---|   |pivot|
    // t[start], ..., t[l], t[r], ..., t[end-1], t[end]
    // 
    int k = partition<T, Comp>( t, start - 1, end, t[end], comp );
    // |----- < pivot----|  |pivot|  |--- >= pivot ---|   
    // t[start], ..., t[l], t[end], ..., t[end-1], t[r]
    //    start         l     k                    end
    std::swap( t[end], t[k] );
    // 对子区域：t[start], ..., t[l]，进行快排
    quick_sort_n<T, Comp>( t, start, k - 1, comp );
    // 对子区域：..., t[end-1], t[r]，进行快排
    quick_sort_n<T, Comp>( t, k + 1, end, comp );
}
// 获得start，end之间的pivot，这里就是取中间。
int InnerSortAlgorithm::findPivot( const int &start, const int &end )
{
    return ( start + end ) / 2;
}
// ************************************************
// 对数组t[start, end)左闭右开区间范围的数进行partition分区
//
// 使得对于所有left partition的数，comp(left, pivotVal)始终成立
// 使得对于所有right partition的数，comp(right, pivotVal)始终不成立
// 举个例子，若comp = 
// [](const int& a, const int& b){
//     return a < b;
// }
// 则left都<pivot，right>=pivot。
// 若改成return a <= b;，则left都<= pivot，right > pivot。
//
// 并返回first index of right partition。
// ************************************************
template<class T, class Comp>
int InnerSortAlgorithm::partition( T t[], const int &start, const int &end, const T &pivotVal, Comp comp )
{
    while( true )
    {
        while( ++start != end && comp( t[start], pivotVal ) );
        while( --end != start && !comp( t[end], pivotVal ) );
        if( start < end ) { std::swap( t[start], t[end] ); }
        else { break; }
    }
    return start;
}

改进

适合大规模数据量，小规模的可以考虑交换排序；
不“分治”小于9的子序，改为改插入排序。
栈代替递归：减少函数调用，当存储的信息不大时。
五、归并排序
```cpp

//对A数组left到right范围元素进行排序。 template void mergesort(Elem A[], Elem temp[], int left, int right){

if(left == right) return;    //不需要归并1个元素数组，
// 归并少于THRESHOLD个元素的数组，直接用插入排序更快。
if((right - left) <= THRESHOLD){
    执行插入排序
    return;
}
int mid = (left + right) >> 1;
// 先对左右两半部分分别进行归并排序
mergesort<Elem, Comp>(A, temp, left, mid);        //对左半部分归并
mergesort<Elem, Comp>(A, temp, mid + 1, right);    //对右半部分归并
// A：   [0, 10, 20, 30,| 0, 1, 2, 3]
// temp：[0, 10, 20, 30,| 3, 2, 1, 0]
for(int i = left; i <= mid; i++) { temp[i] = A[i]; }
for( int i = right; i >= mid + 1; i-- ) { copyArr[mid + right + 1 - i] = arr[i]; }
// A：   [<k> 0, 10, 20, 30,| 0, 1, 2, 3    ]
// temp：[<i> 0, 10, 20, 30,| 3, 2, 1, 0 <j>]
for(int i = left, j = right, k = left; k <= right; k++){
    if(Comp::lt(temp[i] , temp[j])) A[k] = temp[i++];
    else A[k] = temp[j--];
}

}

<a name="sOpc5"></a>
# 六、堆排序
要排序的数直接在一个数组A中全部给定了，这个时候进行建堆就非常简单，排序的过程就是删除根节点的过程，更准确的来讲，是把根节点与堆尾节点对换，再把新的根节点“下沉”来保持堆的结构。
![](https://cdn.nlark.com/yuque/0/2021/gif/461452/1615788162940-f9e36f5b-41b0-448f-8812-e40c7e74ebfc.gif#align=left&display=inline&height=364&margin=%5Bobject%20Object%5D&originHeight=364&originWidth=547&size=0&status=done&style=none&width=547)
```cpp
vector<int> MySort( vector<int> &arr )
{
    if( arr.size() < 2 ) { return arr; }
    Heap heap( arr );
    while( !heap.empty() ) { heap.pop(); }
    return arr;
}
class Heap
{
    public:
    Heap( vector<int> &arr );
    void pop();
    bool empty();
    private:
    void siftDown( const int & );
    int leftChild( const int & );
    int rightChild( const int & );
    bool leaf( const int & );
    private:
    vector<int> &_data;
    int _dataSize;
};
Heap::Heap( vector<int> &arr )
    : _data( arr )
    , _dataSize( arr.size() )
{
    for( int i = ( arr.size() >> 1 ) - 1; i >= 0; i-- ) { siftDown( i ); }
}
void Heap::pop()
{
    if( _dataSize )
    {
        std::swap( _data[0], _data[_dataSize - 1] );
        _dataSize--;
        siftDown( 0 );
    }
}
bool Heap::empty() return _dataSize == 0;
void Heap::siftDown( const int &index )
{
    if( !leaf( index ) )
    {
        int maxChild = leftChild( index );
        int rightchild = rightChild( index );
        if( rightchild < _dataSize && _data[maxChild] < _data[rightchild] )
        {
            maxChild = rightchild;
        }
        if( _data[index] < _data[maxChild] )
        {
            std::swap( _data[maxChild], _data[index] );
            siftDown( maxChild );
        }
    }
}
int Heap::leftChild( const int &index ) return ( index << 1 ) + 1;
int Heap::rightChild( const int &index ) return ( index << 1 ) + 2;
bool Heap::leaf( const int &index ) return index > ( ( _dataSize >> 1 ) - 1 );

性能分析
建堆需要O(n)，1次removemax需要O(log n)，总共需要n次removemax，
因此总代价是O(nlog n)。平均、最佳、最差都是这个。
找出第K大的数，需要时间O(n) + kO(log n) 也就是O(n + k * log n)。

上面算法是建立在数全部已知，且为数不多的情况。
堆更适合外排序。

数据结构与算法_内排序