训练题：复杂链表拷贝

题目：http://t.cn/A6qbIzAu

方法一：递归+哈希

  • 时间复杂度：O（n）
  • 空间复杂度：O（n） ```cpp

Node copyRandomList(Node head) { if(!head) return head;

  1. unordered_map<Node*, Node*> info;
  3. return _copy(info, head);

}

Node _copy(unordered_map<Node, Node>& info, Node node){ if(!node) return nullptr;

  1. Node* copy_node = nullptr;
  2. if(info.count(node)) copy_node = info[node];
  3. else{
  4.     copy_node = copyNode(node);
  5.     info[node] = copy_node;
  6. }
  8. if(!node->random) copy_node->random = nullptr;
  9. else
  10. {
  11.     if(!info.count(node->random)) info[node->random] = copyNode(node->random);
  12.     copy_node->random = info[node->random];
  13. }
  15. copy_node->next = _copy(info, node->next);
  17. return copy_node;

}

Node copyNode(Node node) { if(!node) return nullptr; return new Node(node->val); }

  1. <a name="5lft7"></a>
  2. ## 方法二：迭代+哈希
  4. - 时间复杂度：O（n）
  5. - 空间复杂度：O（n）
  6. ```cpp
  8. Node* copyRandomList(Node* head) {
  9.     if(!head) return head;
  11.     unordered_map<Node*, Node*> info;
  13.     Node copyHead(1), *copyHeadPtr = &copyHead;
  14.     for(Node* node = head; node; node = node->next){
  16.         if(!info.count(node)) info[node] = new Node(node->val);;
  18.         copyHeadPtr->next = info[node];
  19.         copyHeadPtr = copyHeadPtr->next;
  21.         if(!node->random) copyHeadPtr->random = nullptr;
  22.         else{
  23.             if(!info.count(node->random)) info[node->random] = new Node(node->random->val);
  24.             copyHeadPtr->random = info[node->random];
  25.         }
  26.     }
  28.     return copyHead.next;
  29. }

方法三

  • 时间复杂度：O（n）
  • 空间复杂度：O（1） ```cpp

Node copyRandomList(Node head) { if(!head) return head;

  1. Node* node = nullptr, *tmpNode = nullptr;
  3. // 第一步，在原链表每个节点后插入拷贝的节点
  4. // 原链表：node1->node2->node3
  5. // 新链表：node1->copy1->node2->copy2->node3->copy3
  6. for(node = head, tmpNode = nullptr; node; node = tmpNode->next){
  7.     tmpNode = new Node(node->val);
  8.     tmpNode->next = node->next;
  9.     node->next = tmpNode;
  10. }
  12. // 为每个copy node赋值random
  13. // 在新链表中，任意node的next就是它的copy node
  14. for(node = head; node; node = node->next->next){
  15.     if(node->random) node->next->random = node->random->next;
  16. }
  18. // 链表：node1->copy1->node2->copy2->node3->copy3
  19. // 拆分成两个链表：
  20. // 链表1：node1->node2->node3
  21. // 链表2：copy1->copy2->copy3
  22. Node* ret = head->next;
  23. for(node = head, tmpNode = head->next; tmpNode->next;){
  24.     node->next = tmpNode->next;
  25.     node = node->next;
  26.     tmpNode->next = node->next;
  27.     tmpNode = tmpNode->next;
  28. }
  29. node->next = nullptr;
  31. return ret;

}

  1. <a name="1XsV0"></a>
  2. # 训练题：删除链表节点
  3. 题目：[http://t.cn/A6VqjZ1i](http://t.cn/A6VqjZ1i)
  4. ```cpp
  6. ListNode* deleteNode(ListNode* head, int val) {
  7.     if( !head ) { return head; }
  8.     if( head->val == val) { return head->next; }
  10.     ListNode* tmpHead = head, *tmpPre = nullptr;
  12.     for( ; tmpHead && tmpHead->val != val; tmpPre = tmpHead, tmpHead = tmpHead->next ); 
  14.     if( tmpHead ) tmpPre->next = tmpHead->next;
  15.     return head;
  16. }

训练题：逆序打印链表

题目：http://t.cn/A62bSlA8

方法一：递归

  2. vector<int> reversePrint( ListNode* head )
  3. {
  4.     vector<int> shit;
  5.     int count = 0;
  7.     for( ListNode* node = head; node; node = node->next, ++count );
  8.     shit.reserve( count );
  10.     return _reverse( head, shit );
  11. }
  13. vector<int> &_reverse( ListNode* head, vector<int> &container )
  14. {
  15.     if( !head ) { return container; }
  16.     _reverse( head->next, container );
  17.     container.push_back( head->val );
  18.     return container;
  19. }

方法二：迭代（栈）

  2. vector<int> reversePrint(ListNode* head) {
  3.     stack<int> shit;
  4.     int count = 0;
  6.     for( count = 0; head; head = head->next, ++count ) { shit.push( head->val ); }
  8.     vector<int> ret;
  9.     ret.reserve( count );
  10.     for( ; !shit.empty(); shit.pop() ) { ret.push_back( shit.top() ); }
  12.     return ret;
  13. }

训练题：合并链表

场景一：合并两个有序链表

题目：http://t.cn/A6VzAxiN

方法一：迭代

  • 时间复杂度：O(n+m)
  • 空间复杂度：O(1) ```cpp

ListNode mergeTwoLists(ListNode l1, ListNode* l2) { if( !l1 ) { return l2; } if( !l2 ) { return l1; }

  1. // newHead是合并后的表头
  2. // tail是当前迭代过程中的表尾
  3. // tmpNode是l1和l2迭代过程中更小的表头。
  4. // 每一次迭代去取更小的表头，该链表表土也相应位移
  5. ListNode* newHead = nullptr, *tail = nullptr, *tmpNode = nullptr;
  7. while( l1 && l2 )
  8. {
  9.     // 第一步取更小的节点
  10.     if( l1->val < l2->val )
  11.     {
  12.         tmpNode = l1;
  13.         l1 = l1->next;
  14.     }
  15.     else
  16.     {
  17.         tmpNode = l2;
  18.         l2 = l2->next;
  19.     }
  21.     // 第二步，拼接到newHead~tail构成的链表的尾部。
  22.     if( !newHead )
  23.     {
  24.         newHead = tail = tmpNode;
  25.     }
  26.     else
  27.     {
  28.         tail->next = tmpNode;
  29.         tail = tmpNode;
  30.     }
  31. }
  33. if( !l1 ) { tail->next = l2; }    // l1比l2短，直接接上剩余的l2部分
  34. if( !l2 ) { tail->next = l1; }    // 同理
  36. return newHead;

}

  1. <a name="rtATP"></a>
  2. ### 方法二：递归
  3. 时间复杂度：O（n+m）<br />空间复杂度：O（n+m），递归栈空间<br />既然可以迭代，就可以考虑递归
  4. ```cpp
  6. // 先去l1和l2更小的表头，比如是l1
  7. // 则接下来合并l1->next和l2即可，并让l1->next = 新合并的表头即可。
  8. ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
  9.     if( !l1 ) { return l2; }
  10.     if( !l2 ) { return l1; }
  12.     if( l1->val < l2->val )
  13.     {
  14.         l1->next = mergeTwoLists( l1->next, l2 );
  15.         return l1;
  16.     }
  17.     else
  18.     {
  19.         l2->next = mergeTwoLists( l1, l2->next );
  20.         return l2;
  21.     }
  22. }

场景二：合并K个链表

题目：http://t.cn/EAeXgtU

方法一：顺序合并

  • 时间复杂度：O(k2n)
  • 空间复杂度：O(1) ```cpp

ListNode mergeKLists( vector<ListNode> &lists ) { ListNode* head = nullptr; for( auto list : lists ) { head = mergeTwoLists( head, list ); } return head; }

  1. <a name="cQpI8"></a>
  2. ### 方法二：分治合并（递归）
  3. 归并排序的分治思想。
  5. - 时间复杂度：O(kn x logk)
  6. - 空间复杂度：O(log k)
  7. ```cpp
  9. ListNode* mergeKLists(vector<ListNode*>& lists) {
  10.     if(lists.empty()) return nullptr;
  11.     if(lists.size() == 1) return lists[0];
  13.     return merge(lists, 0, lists.size() - 1);
  14. }
  16. ListNode* merge(vector<ListNode*>& lists, int left, int right){
  17.     if(right <= left) return lists[left];
  19.     int mid = left + ((right - left) >> 1);
  21.     ListNode* node1 = merge(lists, left, mid);    
  22.     ListNode* node2 = merge(lists, mid+1, right);
  24.     return mergeTwoLists(node1, node2);
  25. }
  27. ListNode* mergeTwoLists(ListNode* listNode1, ListNode* listNode2){
  28.     if(!listNode1) return listNode2;
  29.     if(!listNode2) return listNode1;
  31.     if(listNode1->val < listNode2->val){
  32.         listNode1->next = mergeTwoLists(listNode1->next, listNode2);
  33.         return listNode1;
  34.     }
  36.     listNode2->next = mergeTwoLists(listNode1, listNode2->next);
  37.     return listNode2;
  38. }

方法三：分治合并（迭代）

有递归，就可以再考虑迭代，这里我们可以借助队列queue实现。

  2. ListNode* mergeKLists( vector<ListNode*> &lists )
  3. {
  4.     if( lists.empty() ) { return nullptr; }
  5.     if( lists.size() == 1 ) { return lists[0]; }
  7.     queue<ListNode*> q;
  9.     for( auto shit : lists ) if( shit ) { q.push( shit ); }
  10. 、
  11.     // 每次迭代去两个出来合并，在插入队列尾部。
  12.     for( ListNode* node1 = nullptr, *node2 = nullptr; q.size() > 1 ; )
  13.     {
  14.         node1 = q.front();
  15.         q.pop();
  16.         node2 = q.front();
  17.         q.pop();
  18.         q.push( mergeTwoLists( node1, node2 ) );
  19.     }
  20.     if( q.empty() ) { return nullptr; }
  21.     return q.front();
  22. }

方法四：优先队列

  2. struct SHIT
  3. {
  4.     ListNode* node;
  6.     SHIT() = default;
  7.     SHIT( ListNode* n ) : node( n ) {}
  9.     bool operator<( const SHIT &shit1 ) const
  10.     {
  11.         return node->val > shit1.node->val;
  12.     }
  13. };
  15. ListNode* mergeKLists( vector<ListNode*> &lists )
  16. {
  17.     priority_queue<SHIT> pq;
  19.     ListNode head;
  21.     for( auto shit : lists ) if( shit ) { pq.push( shit ); }
  23.     for( ListNode* tail = &head; !pq.empty(); )
  24.     {
  25.         SHIT shit = pq.top();
  26.         pq.pop();
  28.         tail->next = shit.node;
  29.         tail = tail->next;
  31.         if( shit.node->next ) { pq.push( shit.node->next ); }
  32.     }
  34.     return head.next;
  35. }

方法五：普通迭代

时间复杂度：O(k2n)
空间复杂度：O(1)

  2. ListNode* mergeKLists( vector<ListNode*> &lists )
  3. {
  4.     if( lists.empty() ) { return nullptr; }
  5.     if( lists.size() == 1 ) { return lists[0]; }
  7.     short tmpIdx      = -1;
  8.     ListNode  head;
  9.     ListNode* tail    = &head;
  10.     ListNode* tmpNode = nullptr;
  12.     for( auto it = lists.begin(); it != lists.end(); )
  13.     {
  14.         if( !*it ) { it = lists.erase( it ); }
  15.         else { ++it; }
  16.     }
  18.     while( !lists.empty() )
  19.     {
  20.         for( short idx = 0, size = lists.size(); idx < size; ++idx )
  21.         {
  22.             if( lists[idx] )
  23.             {
  24.                 if( !tmpNode || ( tmpNode && lists[idx]->val < tmpNode->val ) )
  25.                 {
  26.                     tmpIdx = idx;
  27.                     tmpNode = lists[tmpIdx];
  28.                 }
  29.             }
  30.         }
  32.         if( !lists[tmpIdx]->next ) { lists.erase( lists.begin() + tmpIdx ); }
  33.         else { lists[tmpIdx] = lists[tmpIdx]->next; }
  35.         tail->next = tmpNode;
  36.         tail       = tail->next;
  37.         tmpNode    = nullptr;
  38.     }
  40.     return head.next;
  41. }

训练题：翻转链表

情形一：整个翻转

题目：http://t.cn/A6cFDmo9

方法一：容器逆序

  2. // 方法一：C++ STL容器的逆序
  3. // 时间复杂度：O(n)
  4. // 空间复杂度：O(n)
  5. ListNode* ReverseList( ListNode* pHead )
  6. {
  7.     if( !pHead || !pHead->next ) { return pHead; }
  9.     vector<ListNode*> vNodes;
  10.     while( pHead )
  11.     {
  12.         vNodes.push_back( pHead );
  13.         pHead = pHead->next;
  14.     }
  16.     // 将容器逆序
  17.     reverse( vNodes.begin(), vNodes.end() );
  19.     for( int i = 1; i < vNodes.size(); i++ )
  20.     {
  21.         vNodes[i - 1]->next = vNodes[i];
  22.     }
  23.     vNodes.back()->next = nullptr;
  25.     return vNodes[0];
  26. }

方法二：栈

  2. // 方法二：栈的特性，先入栈，再弹栈。每次弹栈，插入链表尾部。
  3. // 时间复杂度：O(n)
  4. // 空间复杂度：O(n)
  5. ListNode* ReverseList( ListNode* pHead )
  6. {
  7.     if( !pHead || !pHead->next ) return pHead;
  9.     stack<ListNode*> stackNodes;
  10.     while( pHead )
  11.     {
  12.         stackNodes.push( pHead );
  13.         pHead = pHead->next;
  14.     }
  16.     pHead         = stackNodes.top();
  17.     ListNode* cur = pHead;
  18.     stackNodes.pop();
  19.     while( !stackNodes.empty() )
  20.     {
  21.         cur->next = stackNodes.top();
  22.         cur = cur->next;
  23.         stackNodes.pop();
  24.     }
  25.     cur->next = nullptr;
  26.     return pHead;
  27. }

方法三：递归一

  1. // 
  2. // 递归方法一：
  3. // 设某个递归过程中，链表结构如下： * -> * -> cur -> next -> * -> ...
  4. // 递归子过程：
  5. //        1、翻转next起始的链表部分。
  6. //        2、翻转后，next为表尾，将cur接到next之后
  7. // 结果如下：* -> * -> cur <- next <- * <- ...
  8. //
  9. // 整个递归过程是从后往前进行逆序
  10. //
  11. // 时间复杂度：O(n)
  12. // 空间复杂度：O(n)
  13. ListNode* ReverseList( ListNode* pHead )
  14. {
  15.     // 递归终止条件
  16.     if( !pHead || !pHead->next ) { return pHead; }  // 空链表或者只有1个节点。
  18.     // 递归子过程：翻转head链表，就先翻转head->next链表，然后将head放到翻转后的结尾即可。
  19.     ListNode* reverseNode = ReverseList_3( next );  // 翻转后：表头reverseNode，表尾next
  21.     // 将head放到表尾next后面
  22.     pHead->next->next  = pHead;
  23.     pHead->next = nullptr;
  25.     return reverseNode;
  26. }

方法四：递归二

  2. // 递归方法二：当然就是从前往后进行逆序
  3. // 设某个递归过程中，链表结构如下： * <- * <- cur -> next -> * -> ...
  4. // 其中cur往左部分为已逆序部分，next之后部分为链表的原始部分
  5. // 递归一次之后：* <- * <- cur <- next -> * -> ...
  7. // 时间复杂度：O(n)
  8. // 空间复杂度：O(n)
  9. ListNode* ReverseList( ListNode* pHead )
  10. {
  11.     if( !pHead || !pHead->next ) { return pHead; }
  13.     ListNode* nextNode = pHead->next;
  14.     pHead->next        = nullptr;
  16.     // 此时的pHead为首的链表是已逆序链表
  17.     // 而nextNode则为pHead在原链表中的next节点
  18.     return _ReverseList( pHead, nextNode );        // 尾递归，性能比普通递归要好一点
  19. }
  21. // 以curNode为首的链表是已逆序链表
  22. // nextNode为curNode在原链表中的next节点
  23. // 这里要做的就是把nextNode插入逆序链表中，使得其还是逆序，非常简单，
  24. // nextNode->next = curNode即可。则nextNode又是一个逆序链表
  25. ListNode* _ReverseList( ListNode* curNode, ListNode* nextNode )
  26. {
  27.     if( !nextNode ) { return curNode; }
  28.     ListNode* newNextNode = nextNode->next;
  29.     nextNode->next        = curNode;
  30.     return _ReverseList( nextNode, newNextNode );
  31. }

方法五：迭代

  2. // 方法五：其实就是用迭代代替递归过程。
  3. // 时间复杂度：O(n)
  4. // 空间复杂度：O(1)
  5. ListNode* ReverseList( ListNode* pHead )
  6. {
  7.     if( !pHead || !pHead->next ) { return pHead; }
  9.     // pReverseHead    逆序链表的表头
  10.     // pHead        当前迭代的节点
  11.     // tmpNext        下一节点
  12.     // 把pHead插入到pReverseHead的表头，pHead又是一个逆序链表。
  13.     // tmpNext保存了下一节点，然后继续下一个迭代。
  14.     ListNode* pReverseHead = nullptr;
  15.     ListNode* tmpNext      = nullptr;
  16.     while( pHead )
  17.     {
  18.         tmpNext      = pHead->next;
  19.         pHead->next  = pReverseHead;
  20.         pReverseHead = pHead;
  21.         pHead        = tmpNext;
  22.     }
  23.     return pReverseHead;
  24. }

情形二：k个一组翻转

题目：http://t.cn/A6VzVlse

方法一：栈

  2. ListNode* reverseKGroup( ListNode* head, int k )
  3. {
  4.     // k = 0 / 1时，返回原数组
  5.     // head为空或者只有1个元素时，返回原数组
  6.     if( k < 2 || !head || !head->next ) { return head; }    
  8.     ListNode* newHead         = nullptr;    // 新链表的表头
  9.     ListNode* tmpNodeStack    = nullptr;    // 栈遍历的tmpNode
  10.     ListNode* tail            = nullptr;    // 新链表的表尾
  11.     ListNode* oldHead          = nullptr;    // 在栈中原链表顺序的表头，即栈底元素
  13.     stack<ListNode*> s;                        // 栈
  15.     for( ListNode* tmpNode = head; tmpNode; )
  16.     {
  17.         oldHead = tmpNode;
  19.         while( s.size() < k && tmpNode )    // 每次压栈k个元素
  20.         {
  21.             s.push( tmpNode );
  22.             tmpNode = tmpNode->next;
  23.         }
  25.         if( s.size() == k )                    // 压满，则全部弹栈，构成newHead为表头，tail为表尾的新链表
  26.         {
  27.             while( !s.empty() )
  28.             {
  29.                 tmpNodeStack = s.top();
  30.                 s.pop();
  32.                 if( !newHead ) { newHead = tmpNodeStack; }
  34.                 if( !tail ) { tail = tmpNodeStack; }
  35.                 else
  36.                 {
  37.                     tail->next = tmpNodeStack;
  38.                     tail = tail->next;
  39.                 }
  40.             }
  41.             tail->next = nullptr;
  42.         }
  43.         else if(!s.empty())                    // 栈中元素不够k个，按原链表顺序。
  44.         {
  45.             if( !newHead ) { newHead = head; }                        // 整个链表的数量都小于K个，链表原样输出
  46.             else if( oldHead && tail ) { tail->next = oldHead; }    // 将栈中的链表部分的头部oldHead接入到新链表表尾tail
  47.         }
  48.     }
  50.     return newHead;
  51. }

方法二：递归

  2. ListNode* reverseKGroup( ListNode* head, int k )
  3. {
  4.     // k = 0 / 1时，返回原数组
  5.     // head为空或者只有1个元素时，返回原数组
  6.     if( k < 2 || !head || !head->next ) { return head; }
  8.     ListNode* tail = head;
  9.     for( int i = 0; i < k ; i++ )
  10.     {
  11.         if( !tail ) { return head; }
  12.         tail = tail->next;
  13.     }
  15.     // 链表初始状态
  16.     // |---------k----------|
  17.     // head, ..., tail1, tail, ...
  19.     // 翻转[head, tail)左闭右开区间，返回的表头tail1
  20.     // |---------k----------|
  21.     // tail1, ..., head, tail, ...
  22.     ListNode* newHead = reverse( head, tail );
  24.     // 在翻转[tail, ...)区间，令head->next等于其表头
  25.     head->next = reverseKGroup( tail, k );
  27.     return newHead;
  28. }
  30. // 翻转链表：head, ..., tail1, tail
  31. // 得到结果：tail1, ..., head, tail
  32. // 返回tail1
  33. ListNode* reverse( ListNode* head, ListNode* tail )
  34. {
  35.     if( head == tail ) { return head; }
  37.     ListNode* pre = nullptr, *next = nullptr;
  38.     while( head != tail )
  39.     {
  40.         next = head->next;
  41.         head->next = pre;
  42.         pre = head;
  43.         head = next;
  44.     }
  45.     return pre;
  46. }

训练题：链表环

题目：http://t.cn/A6VZ6gl2

方法一：快慢指针

  • 时间复杂度：O(n)
  • 空间复杂度：O(1) ```cpp

bool hasCycle(ListNode *head) { if( !head || !head->next || !head->next->next ) { return false; }

  1. for(ListNode* slow = head, *fast = head; fast && fast->next;){
  2.     if( slow ) slow = slow->next;
  3.     fast = fast->next->next;
  4.     if(slow == fast) return true;
  5. }
  7. return false;

}

  1. <a name="7yMPm"></a>
  2. ## 方法二：set集合
  4. - 时间复杂度：O(n)
  5. - 空间复杂度：O(n)
  6. ```cpp
  8. // 将所有节点记录到集合中，如果有重复，则包含环。
  9. bool hasCycle(ListNode *head) {
  10.     set<ListNode*> s;
  11.     while(head){
  12.         if(s.count(head)) return true;
  13.         s.insert(head);
  14.         head = head->next;
  15.     }
  16.     return false;
  17. }

方法三：删除表头

  • 时间复杂度：O(n)
  • 空间复杂度：O(1) ```cpp

bool hasCycle(ListNode *head) {

  1. // 迭代删除表头head，且令head->next = head
  2. // 若没有环，则表会被全部删除
  3. // 若有环，则最终会出现head == head->next
  4. for(ListNode* tmpNode = nullptr; head;)
  5. {
  6.     if( head && head == head->next ) { return head; }
  7.     tmpNode = head->next;
  8.     head->next = head;
  9.     head = tmpNode;
  10. }
  11. return false;

}

  1. <a name="8ssuZ"></a>
  2. # 训练题：倒数第K节点
  3. 题目：[http://t.cn/A6VZCfdr](http://t.cn/A6VZCfdr)
  4. <a name="xv1Al"></a>
  5. ## 情形一：找出倒数第K节点
  6. <a name="SLaJi"></a>
  7. ### 方法一：统计链表长度
  9. - 时间复杂度：O(n) + O(n-k)
  10. - 空间复杂度：O(1)
  11. ```cpp
  13. ListNode* FindKthToTail(ListNode* pHead, int k) {
  14.     if( k <= 0 ) { return nullptr; }
  16.     int count = 0;
  17.     for(ListNode* tmp = pHead; tmp; tmp = tmp->next, ++count);
  19.     if(count < k) return nullptr;
  21.     int n_k = count - k;
  22.     for(ListNode* tmp = pHead;; n_k--, tmp = tmp->next){
  23.         if(!n_k) return tmp;
  24.     }
  25. }

方法二：双指针

  • 时间复杂度：O(n)
  • 空间复杂度：O(1) ```cpp

ListNode FindKthToTail(ListNode pHead, int k) { if( k— <= 0 ) { return nullptr; }

  1. // first和second之间距离相隔K个节点，当first到达链表尾部，second即是倒数第K个节点
  2. ListNode* first = pHead, *second = pHead;
  3. while( k-- && first ) { first = first->next; }
  5. if( !first ) { return nullptr; }    // 链表没有K个节点，返回空。
  7. while( first->next )
  8. {
  9.     first  = first->next;
  10.     second = second->next;
  11. }
  12. return second;

}

  1. <a name="1PAiW"></a>
  2. ## 情形二：删除倒数第K节点
  3. <a name="85eAN"></a>
  4. ### 方法一：统计链表长度
  5. 原理同上面方法一。
  6. <a name="Fpup3"></a>
  7. ### 方法二：双指针
  8. ```cpp
  10. ListNode* removeNthFromEnd(ListNode* head, int n) {
  12.     // first和second之间距离相隔K个节点，当first到达链表尾部，second即是倒数第K个节点
  13.     // beforeSecond是second之前的节点
  14.     ListNode* first = head, *second = head, *beforeSecond = nullptr;
  16.     while( n-- > 1 ) { first = first->next; }
  18.     while( first->next )
  19.     {
  20.         first = first->next;
  21.         beforeSecond = second;
  22.         second = second->next;
  23.     }
  25.     if( !beforeSecond ) { head = head->next; }        // 删除的是表头
  26.     else { beforeSecond->next = second->next; }        // 删除非表头
  28.     return head;
  29. }

训练题：链表环入口

题目：http://t.cn/A6VZN4eu

方法一：集合set

  • 时间复杂度：O(n)
  • 空间复杂度：O(n) ```cpp

ListNode detectCycle(ListNode head) { set s; while( head ) { if( s.count( head ) ) { return head; } s.insert( head ); head = head->next; } return head; }

  1. <a name="fGR4u"></a>
  2. ## 方法二：删除链表头
  4. - 时间复杂度：O(n)
  5. - 空间复杂度：O(1)
  6. ```cpp
  8. ListNode *detectCycle(ListNode *head) {
  9.     // 迭代删除表头head，且令head->next = head
  10.     // 若没有环，则表会被全部删除
  11.     // 若有环，则最终会出现head == head->next
  12.     for( ListNode* tmpNode = nullptr; head; )
  13.     {
  14.         if( head && head == head->next ) { return head; }
  15.         tmpNode = head->next;
  16.         head->next = head;
  17.         head = tmpNode;
  18.     }
  19.     return nullptr;
  20. }

方法三：快慢指针

  • 时间复杂度：O(n)
  • 空间复杂度：O(1)

算法训练_链表 - 图1
算法训练_链表 - 图2

结论：slow指针从Y开始走一圈之内就会被fast指针追上。
证明：设slow指针在Y位置时，fast指针在Z位置，从Z顺时针到Y的距离为c，我们想象fast指针“追赶”slow指针，slow每走一步，之间的距离就会减少1，也就是说slow从Y位置走c步，fast指针就追赶上了slow，显然c<=b+c，得证。

因此n1=0，有a=(b+c)*n2-b。这句话用现实意义表达就是：

设有有两个速度一样的指针（一次移动一个节点）p1、p2，p1从X出发，p2从Z顺时针出发，当p1到达Y时，走过的路程为a，此时p2也到达了Y。（先转n2圈，然后再（逆时针）回退距离b）。

综上，两个速度一样的指针，一个从链表头出发，一个从快慢指针的相遇点出发，最终会在环入口相遇。

  2. ListNode *detectCycle(ListNode *head) {
  3.     if( !head || !head->next || !head->next->next ) { return nullptr; }
  5.     // 快慢指针找到环
  6.     for( ListNode* slow = head, *fast = head; fast && fast->next; )
  7.     {
  8.         if( slow ) { slow = slow->next; }
  9.         fast = fast->next->next;
  10.         if( slow == fast ) // 有环。
  11.         {
  12.             slow = head;
  13.             for(; slow != fast; slow = slow->next, fast = fast->next);
  14.             return slow;
  15.         }
  16.     }
  17.     return nullptr;
  18. }

训练题：链表公共节点

题目：http://t.cn/A6VA4ArJ

方法一：set集合

  2. ListNode* FindFirstCommonNode( ListNode* pHead1, ListNode* pHead2 )
  3. {
  4.         if( !pHead1 || !pHead2 ) { return nullptr; }
  6.         set<ListNode*> dataSet;
  8.         // 从两个表头同时开始遍历，保存到set中，一旦发现已存在，则表示找到第一公共节点
  9.         while( pHead1 || pHead2 )
  10.         {
  11.             if( pHead1 )
  12.             {
  13.                 if( dataSet.count( pHead1 ) ) { return pHead1; }
  14.                 dataSet.insert( pHead1 );
  15.                 pHead1 = pHead1->next;
  16.             }
  17.             if( pHead2 )
  18.             {
  19.                 if( dataSet.count( pHead2 ) ) { return pHead2; }
  20.                 dataSet.insert( pHead2 );
  21.                 pHead2 = pHead2->next;
  22.             }
  23.         }
  24.         return nullptr;
  25. }

方法二：移动到相同长度位置

  2. struct ListNode* FindFirstCommonNode( struct ListNode* pHead1, struct ListNode* pHead2 )
  3. {
  4.     if( !pHead1 || !pHead2 ) { return nullptr; }
  6.     // 链表长度
  7.     const auto len1 = findListLength( pHead1 );
  8.     const auto len2 = findListLength( pHead2 );
  10.     // 将长的链表头移动到和短链表头长度一样的地方。
  11.     if( len1 != len2 )
  12.     {
  13.         if( len1 > len2 ) { pHead1 = walkStep( pHead1, len1 - len2 ); }
  14.         else { pHead2 = walkStep( pHead2, len2 - len1 ); }
  15.     }
  17.     // 然后同时移动，这两个表头必定会在公共节点相遇
  18.     for( ; pHead1; pHead1 = pHead1->next, pHead2 = pHead2->next )
  19.     {
  20.         if( pHead1 == pHead2 ) { return pHead1; }
  21.     }
  22.     return nullptr;
  23. }
  25. int findListLength( struct ListNode* pHead1 )
  26. {
  27.     if( !pHead1 ) { return 0; }
  28.     int sum = 0;
  29.     while( ( ++sum ) && ( pHead1 = pHead1->next ) );
  30.     return sum;
  31. }
  32. struct ListNode* walkStep( struct ListNode* pHead1, int step )
  33. {
  34.     while( step-- ) { pHead1 = pHead1->next; }
  35.     return pHead1;
  36. }

方法三：构造相同长度链表

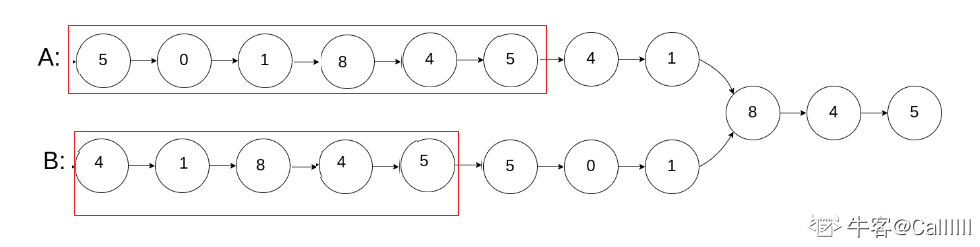
算法训练_链表 - 图3

  2. ListNode* FindFirstCommonNode( ListNode* pHead1, ListNode* pHead2) {
  3.     if( !pHead1 || !pHead2 ) { return nullptr; }
  5.     ListNode* node1 = pHead2, *node2 = pHead1;
  6.     while( node1 != node2 )
  7.     {
  8.         node1 = node1 ? node1->next : pHead1;
  9.         node2 = node2 ? node2->next : pHead2;
  10.     }
  11.     return node1;
  12. }

训练题：链表相加

题目：http://t.cn/A6VAJ1hk

方法一：栈

数字相加，最好从最低位开始加，因此最好从链表的表尾逆序。我们想到的第一个办法是借助栈来实现链表的逆序

  2. ListNode* addInList( ListNode* head1, ListNode* head2 )
  3. {
  4.     if( !head1 ) { return head2; }
  5.     if( !head2 ) { return head1; }
  7.     // 两个栈分别保存，然后不断弹栈依次相加，做到从低位往高位依次相加的顺序。
  8.     // 我们将结果保存到较长的链表中，如果最后还有一个进位，则用较短链表的一个节点接上。
  9.     stack<ListNode*> set1, set2;
  10.     stack<ListNode*> *bigSet = &set1, *smallSet = &set2;    // bigSet指向更长链表的栈
  11.     ListNode* headLong    = head1;        // 指向更长链表的表头
  12.     ListNode* backupNode = nullptr;        // 指向更短链表的表尾，用于最高相加之后还有1个进位时，需再加一个节点。
  14.     for( ListNode* node1 = head1; node1; node1 = node1->next ) { set1.push( node1 ); }
  15.     for( ListNode* node2 = head2; node2; node2 = node2->next ) { set2.push( node2 ); }
  17.     if( set1.size() < set2.size() )
  18.     {
  19.         bigSet     = &set2;
  20.         smallSet   = &set1;
  21.         headLong    = head2;
  22.         backupNode = smallSet->top();
  23.     }
  25.     int carry = 0;        //进位，1/0
  27.     // 先根据更短链表进行遍历，然后将结果保存到更长的链表中
  28.     for( int tmp = 0; !smallSet->empty(); smallSet->pop(), bigSet->pop() )
  29.     {
  30.         tmp = bigSet->top()->val + smallSet->top()->val + carry;
  31.         bigSet->top()->val = tmp % 10;
  32.         carry = tmp / 10;
  33.     }
  35.     // 再遍历更长的链表
  36.     for( int tmp = 0; !bigSet->empty(); bigSet->pop() )
  37.     {
  38.         tmp = bigSet->top()->val + carry;
  39.         bigSet->top()->val = tmp % 10;
  40.         carry = tmp / 10;
  41.     }
  43.     // 最后还有一个进位，需额外接入一个节点到更长链表的表头。
  44.     if( carry )
  45.     {
  46.         backupNode->val = 1;
  47.         backupNode->next = headLong;
  48.         headLong = backupNode;
  49.     }
  50.     return headLong;
  51. }

方法二：翻转链表

除了借助栈，我们还可以自己先翻转链表，然后再翻转回来。

  2. // 翻转链表
  3. ListNode* reverseList( ListNode* head, int &count )
  4. {
  5.     count = 0;
  6.     ListNode* pre = nullptr;
  7.     ListNode* next = !head ? head : head->next;
  8.     while( head )
  9.     {
  10.         ++count;
  11.         head->next = pre;
  12.         pre = head;
  13.         head = next;
  14.         if( next ) { next = next->next; }
  15.     }
  16.     return pre;
  17. }
  19. ListNode* addInList( ListNode* head1, ListNode* head2 )
  20. {
  21.     if( !head1 ) { return head2; }
  22.     if( !head2 ) { return head1; }
  23.     if( head1 == head2 ) { return nullptr; }
  25.     ListNode* backupNode = head2;        // 同上，一个备份节点，用于最后还有1个进位的情况
  26.     ListNode* rHeadLong1 = nullptr;        // 翻转后的更长链表的表头
  27.     int  count1 = 0, count2 = 0;        // 用于判断哪个链表更长
  28.     int  carry           = 0;            // 进位
  29.     auto rHeadLong2      = rHeadLong1 = reverseList( head1, count1 );    // 翻转后更长的链表表头
  30.     auto rHeadShort      = reverseList( head2, count2 );                // 翻转后更短的链表表头
  32.     if( count1 < count2 )
  33.     {
  34.         std::swap( rHeadLong2, rHeadShort );
  35.         rHeadLong1 = rHeadLong2;
  36.         backupNode = head1;
  37.     }
  39.     // 先遍历更短的链表
  40.     for( int tmp = 0; rHeadShort; rHeadLong2 = rHeadLong2->next, rHeadShort = rHeadShort->next )
  41.     {
  42.         tmp             = rHeadLong2->val + rHeadShort->val + carry;
  43.         rHeadLong2->val = tmp % 10;
  44.         carry           = tmp / 10;
  45.     }
  47.     // 再遍历更长的链表
  48.     for( int tmp = 0; rHeadLong2; rHeadLong2 = rHeadLong2->next )
  49.     {
  50.         tmp             = rHeadLong2->val + carry;
  51.         rHeadLong2->val = tmp % 10;
  52.         carry           = tmp / 10;
  53.     }
  55.     // 遍历完成将更长的链表再翻转
  56.     rHeadLong1 = reverseList( rHeadLong1, count1 );
  58.     // 最后还有一个进位的情况
  59.     if( carry )
  60.     {
  61.         backupNode->val  = 1;
  62.         backupNode->next = rHeadLong1;
  63.         rHeadLong1 = backupNode;
  64.     }
  66.     return rHeadLong1;
  67. }

训练题：LRU机制

题目：https://leetcode-cn.com/problems/lru-cache/

  2. // 双向链表
  3. class DoubleLinkNode{
  4. public:
  5.     DoubleLinkNode() = default;
  6.     virtual ~DoubleLinkNode() = default;
  8.     DoubleLinkNode(const int& key, const int& val, DoubleLinkNode* pre = nullptr, DoubleLinkNode* next = nullptr)
  9.         : key(key)
  10.         , val(val)
  11.         , pre(pre)
  12.         , next(next) {}
  13. public:
  14.     int val;
  15.     int key;
  16.     DoubleLinkNode* pre;
  17.     DoubleLinkNode* next;
  18. };
  20. class LRUCache {
  21. public:
  22.     LRUCache(int capacity)
  23.     : _capacity(max(capacity, 1))
  24.     , _tail(nullptr){}
  26.     int get(int key) {
  27.         if(!dataContainer.count(key)) return -1;    // 数据不存在
  28.         dataUsed(key);                                // 使用过了，将其放在链表尾部
  29.         return dataContainer[key]->val;                
  30.     }
  32.     void put(int key, int value) {
  33.         if(dataContainer.count(key)) {
  34.             dataContainer[key]->val = value;
  35.             dataUsed(key);                            // 使用过了，将其放在链表尾部
  36.         }
  37.         else {
  38.             if(dataContainer.size() == _capacity) handleOverload();        // 超载，清除链表首元素，也就是最远未使用元素
  39.             dataContainer[key] = new DoubleLinkNode(key, value);        // 创建数据节点
  40.             dataAdded(key);                                                // 放在链表尾部，这是最近使用过的元素
  41.         }
  42.     }
  44. private:
  46.     // 数据超载，清除最远未使用元素，也就是链表首部的元素
  47.     void handleOverload(){
  48.         if(!_head.next) return;
  51.         DoubleLinkNode* nodeToDel = _head.next;        // 要删除的元素
  52.         DoubleLinkNode* next = nodeToDel->next;        // 该元素的next元素
  54.         // 衔接删除节点后的链表
  55.         _head.next = next;
  56.         if(next) next->pre = &_head;
  58.         dataContainer.erase(nodeToDel->key);        // 清除数据
  60.         if(_tail == nodeToDel) _tail = nullptr;        // 删除的刚好是尾部元素，即双向链表只有一个元素
  62.         delete nodeToDel;                            // 别忘了释放内存
  63.     }
  65.     // 添加了数据，应在双向链表尾部添加该元素
  66.     void dataAdded(const int& key){
  67.         DoubleLinkNode* tmpNode = dataContainer[key];
  69.         if(!_tail){
  70.             _tail = tmpNode;
  71.             _head.next = _tail;
  72.             _tail->pre = &_head;
  73.             _tail->next = nullptr;
  74.             return;
  75.         }
  77.         _tail->next = tmpNode;
  78.         tmpNode->pre = _tail;
  79.         tmpNode->next = nullptr;
  80.         _tail = tmpNode;
  81.     }
  83.     // 数据使用过，则将该数据对应的节点放到链表尾部
  84.     void dataUsed(const int& key){
  85.         DoubleLinkNode* tmpNode = dataContainer[key];
  87.         if(tmpNode == _tail) return; 
  89.         DoubleLinkNode* pre = tmpNode->pre;
  90.         DoubleLinkNode* next = tmpNode->next;
  91.         pre->next = next;
  92.         if(next) next->pre = pre;
  94.         _tail->next = tmpNode;
  95.         tmpNode->pre = _tail;
  96.         tmpNode->next = nullptr;
  97.         _tail = tmpNode;
  98.     }
  100. private:
  101.     int _capacity;            // 数据容量，超过则需要删除最远未使用元素
  103.     // 双向链表，越往后则表示数据是越近被访问，即首元素为最远未使用元素。
  104.     DoubleLinkNode  _head;    // 链表虚拟首部，一直存在，_head->next才是首元素
  105.     DoubleLinkNode* _tail;    // 链表尾部，方便尾部添加
  107.     // 数据容器
  108.     std::unordered_map<int, DoubleLinkNode*> dataContainer;
  109. };