一、矩阵形式
- 优点
- 缺点
二、欧拉角
三、四元数

位置其实本质就是位移（向量），因为不存绝对坐标来描述位置，都是通过一个特定的参考系来描述，即通过描述坐标原点位移了多少到达该位置。
方位也可以一样理解，不存在绝对方位，都是通过一个“单位/源”方位通过一定的旋转到达新方位，这个旋转的量就是角位移。方向（direction），方位（orientation）。
方位的本质是角位移。
位置 + 位移 = 新位置
方位 + 角位移 = 新方位

方位的描述有以下几种方法：

矩阵形式
欧拉角
四元数
一、矩阵形式
方位就是老方位通过旋转（变换）得到，很自然地想到使用矩阵（变换）。阶矩阵的3个行向量，就是用其他坐标系表示新坐标系的三个基向量。
我们通过一个坐标系到另一个坐标系的变换来确定一个方位。矩阵就是这个变换的具体细节。
旋转矩阵是正交的，所以矩阵转置即可求得逆转换。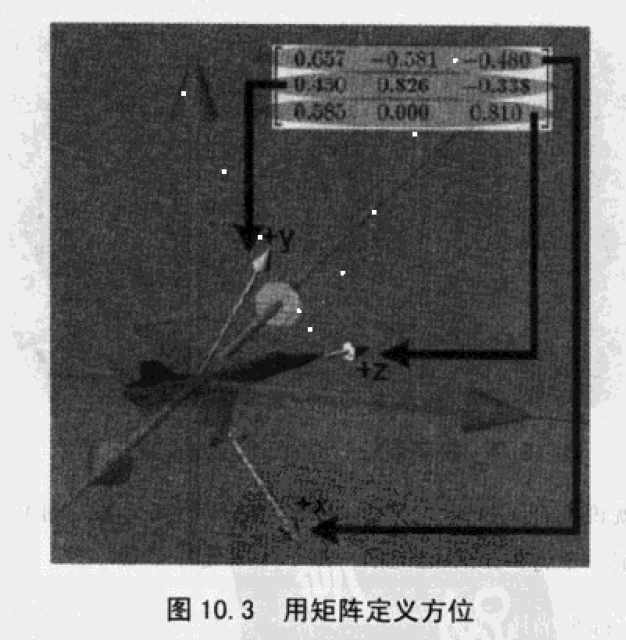

优点
矩阵是一种非常直接的描述方位的形式。

可以立即进行向量的旋转。
图形API只接受矩阵参数。
支持方位嵌套
- 矩阵乘法性质决定了，通过
很容易得到“逆”方位
- 因为旋转矩阵是“正交”的，所以通过矩阵转置即可得到矩阵的逆，也就是说：
- 缺点
数据冗余
- 理论上只需要3个数就能确定方位，矩阵实际上使用了9个数，造成内存的浪费。
难于使用
- 矩阵对于人类并不直观，人脑更擅长理解角度。
“病态矩阵”
- 矩阵使用9个数，其实只有3个数是必需的。也就是说，矩阵带有六阶冗余。描述方位的矩阵必须满足6个限制条件。必须是正交矩阵即，行必须是单位向量，必须互相垂直。随机的9个数，很可能就不满足，导致问题。出现原因如下：
  - 矩阵还可能包含缩放、切变或镜像的操作，这些操作会对物体的“方位” 产生什么影响呢？确实，对此没有一个清晰的定义。任何非正交的矩阵都不是一个定义良好的旋转矩阵。虽然镜像矩阵也是正交的，但它不是有效的旋转矩阵。
  - 可能从外部数据源获得“坏”数据。例如，使用物理数据获取设备（如动作捕捉器）时，捕获过程中可能产生错误。许多建模包就是因为会产生病态矩阵而变得声名狼藉。
  - 可能因为浮点数的舍入错误产生“坏”数据。例如，对一个方位作大量的加运算，这在允许人们手动控制物体方位的游戏中是很常见的。由于浮点精度的限制，大量的矩阵乘法最终可能导致病态矩阵。这种现象称作“矩阵蠕变”。矩阵正交化能解决矩阵蠕变的问题
    二、欧拉角
    欧拉角思想：，这里的x、y、z轴可以是任意的三个轴任意顺序，最典型的还是笛卡尔坐标系并按一定顺序组成的旋转序列。
    heading-pitch-bank
    这是最常用的约定。
    基本思想：
    1、
    2、物体起始在“标准”方位：物体坐标轴与惯性坐标轴对齐。
    3、通过heading旋转+pitch旋转+bank旋转，到达指定方位。
    具体过程：
    1、坐标空间约定
    选择左手坐标系：+x向右，+y向上，+z向前。
    从坐标轴的正方向往原点看，顺时针方向旋转为正向旋转。
    2、heading旋转：绕物体坐标系的y轴旋转量。
    3、pitch旋转：绕物体坐标系的x轴旋转量。
    4、bank旋转：绕物体坐标的z轴的旋转量。
    注意，是绕物体坐标系旋转，不是惯性坐标系，每旋转一次，物体坐标系都发生变化。
    
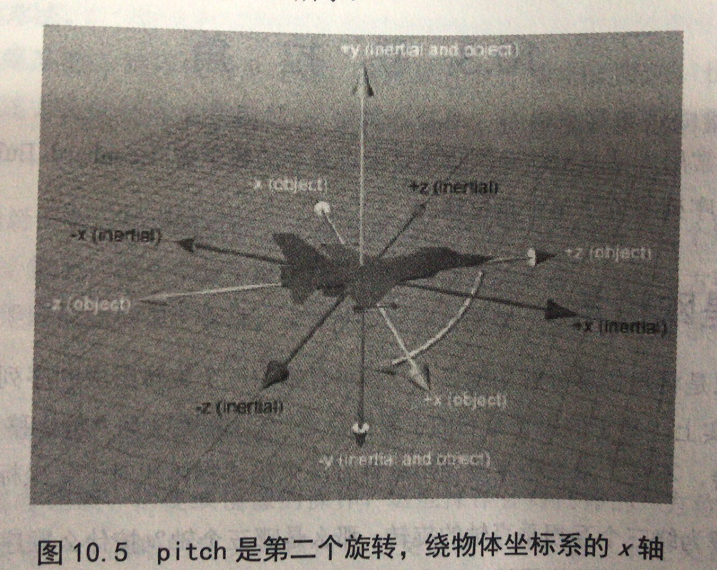
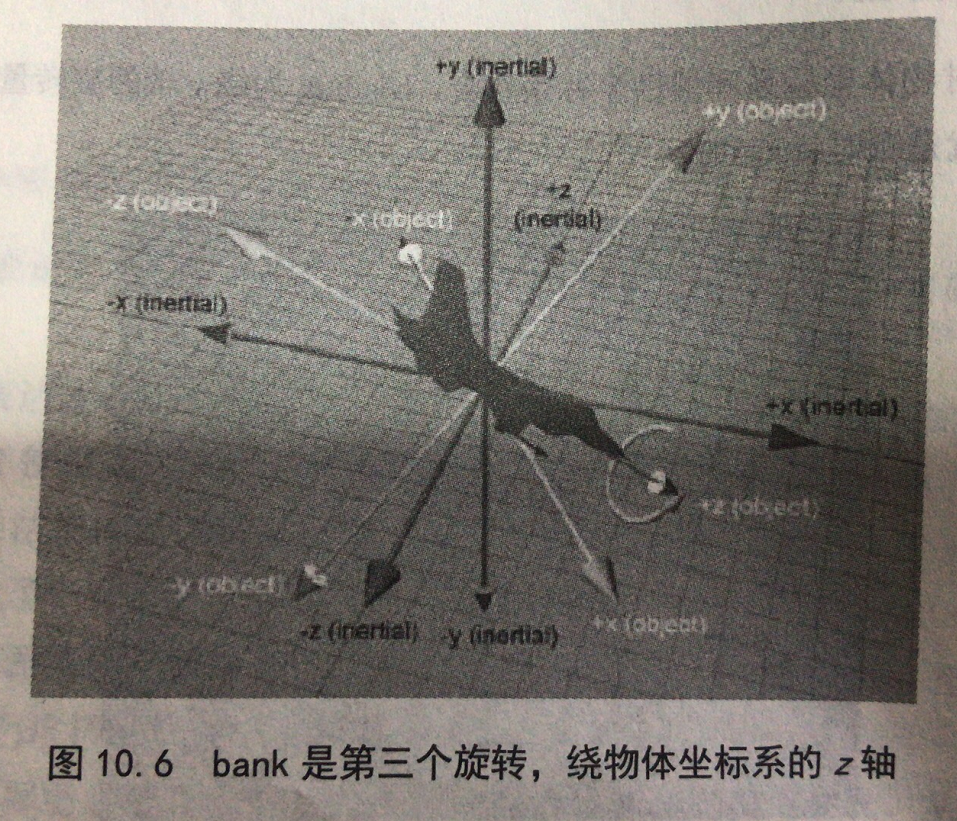
    约定
    heading-pitch-bank系统并不是唯一的欧拉角系统，绕任意三个互相垂直轴的任意旋转序列都能定义一个方位。所以多种选择导致了欧拉角约定的多样性。
    1、heading-pitch-bank系统有多个名称，不同名称对应不同约定，比如roll-pitch-yaw，基本等价于bank-pitch-heading，它定义了向量从物体坐标系变换到惯性坐标系的旋转顺序。
    2、任意三个垂直轴都能作为旋转轴，笛卡尔坐标轴最有意义。
    3、决定每个旋转的正方向时不一定必须遵守左手或右手法则。例如，完全可以定义pitch的正方向是向上的，并且这种定义方法非常常见。
    4、旋转的顺序可以调整，这并不重要。但是heading-pitch-bank最实用。heading绕y轴旋转，在实践中就是在“地面”转。
    优点
    易于理解和使用
    只用了三个数，而且都是角度，对于人脑来说非常容易理解。
    表达方式也很简单，三个数，考虑内存的话，这个最省内存。
    任意数值都合法
    这三个数取任意值都能构成合法欧拉角，只不过可能不是正确的欧拉角。
    缺点
    表达方式不唯一
    同一个方位，可以有很多表达方式，这样就会有这样一个问题“这两组欧拉角是表示相同方位吗？”
    三个角度互相不独立
    比如pitch 135°=heading 180°+pitch 45°+bank 180°。解决办法是限制数值范围：