多边形网格就是一个多边形列表,三角网格就是全部由三角形组成的多边形网格。任意多边形可以分解为三角形。
多边形/三角网格在图形学和建模中广泛使用,用来模拟复杂物体的表面。
一、表示形式
简单表示
多边形网格本质就是一个多边形列表,所以直接用数组来表示三角形网格。
struct Triangle{ // 三个顶点构成三角形Vector3 p[3]; // 三个顶点的坐标}struct TriangleMesh{int count; // 三角形数量Triangle *trilist; // 三角形列表}
这种表示方法只有顶点信息,并没有包含三角形都和其他三角形共享边的信息。有效的三角网格需要存储三类信息:
- 顶点表
- 每个顶点
- 3D坐标
- 附加数据
- 纹理映射坐标
- 表面法向量
- 光照值
- 每个顶点
- 三角形表
- 每个三角形
- 3个顶点的索引,顺序很重要,用于确定正反面。
- 表面法向量(预先计算)
- 表面属性(纹理映射) ```cpp struct Vertex { // 顶点级信息 Vector3 p; // 顶点的3D坐标 …… // 附加数据,如纹理映射坐标,表面法向量,光照值等 }
- 每个三角形
struct Triangle { // 三角形级的信息 int vertex[3]; // 顶点列表 …… // 附加数据,如法向量、材质信息。 }
struct TriangleMesh{ // 索引三角网格 int vertexCount; // 顶点数 Vertex *vertexList; // 顶点表,包含了顶点的索引信息。
int triangleCount; // 三角形数Triangle *triangleList; // 三角形表
}; ``` 总结起来就是,顶点表保存所有的顶点,三角形表构建这些顶点的“三角关系”。
改进
简单的索引三角网格对基本应用已经足够,但还可以改进实现更加高效的操作。主要问题是没有显示表达邻接信息,必须从三角形列表中搜索,既然这样,我们干脆改成保存边信息,而不是顶点信息:
- 边列表
- 每条边:两个顶点
- 三角形表
- 每个三角形:三条边索引
称为“winged edge”模型。
大多数图形卡并不直接支持索引三角网。渲染三角形时,一般是将三个顶点同时提交。这样,共享顶点会多次提交,三角形用到一次就提交一次。许多API和硬件支持特殊的三角网格式以减少传输量。基本思想是排序点和面,使得显存中已有的三角形不需要再次传输。共有三种方案:
- 顶点缓存
- 三角带
- 三角扇
顶点缓存
GPU缓存一小部分最近使用的顶点,当API要发送顶点时,先检测缓存是否命中,没有命中才发送顶点,并更新缓存。这是底层优化,高级应用代码不需要考虑缓存问题。
善用缓存,可能使发送到显卡的顶点数降低到平均每三角形少于一个。三角带
三角带是一个三角形列表,其中每个三角形都与前一个三角形共享一边。
注意顶点列出的顺序使得每三个连续的点都能构成一个三角形。
顶点顺序在顺时针和逆时针间不断变换,某些平台上,需要指出第一个三角形的顶点顺序,而有些平台上顺序是固定的。
最佳情况下,三角带可用n+2个顶点存储n个面,n很大时,每个三角形平均发送一个顶点。
有些网格是三角带无法表达的。
三个以上三角形共享的顶点依然要被发送多次。
如果用三角带来表示一个三角网格,需要的顶点数目为:
为了使顶点数尽量少,应该使三角带数目越少长度越长越好,因为初始的三角带需要3个顶点,而后续是一个顶点对应一个三角形。
另外建立三角带需要时间:
所以三角带数目越少越好,长度越长越好。
我们可以使用退化三角形(面积=0)来连接多个三角形,从而使整个网格置于一个连续的三角带中。如下: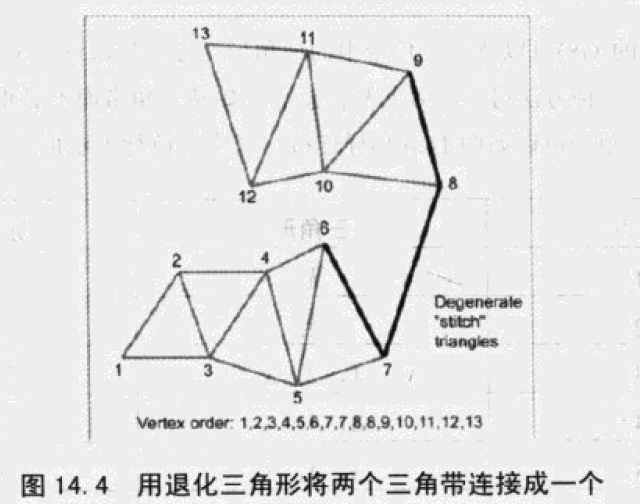
三角带顶点顺序为:
1,2,3,4,5,6,7,7,8,8,9,10,11,12,13
这符合我们每三个连续顶点表示一个三角形的约定。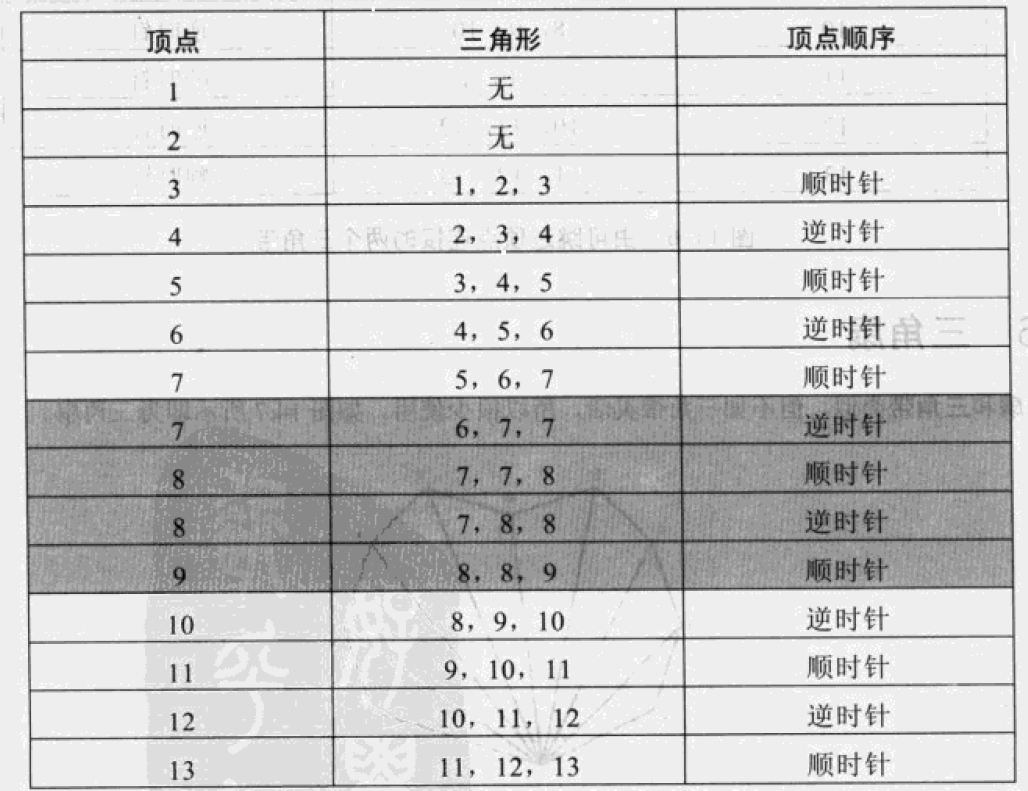
部分硬件可以跳过三角带中的三角形,根据以上情况,结果将如下: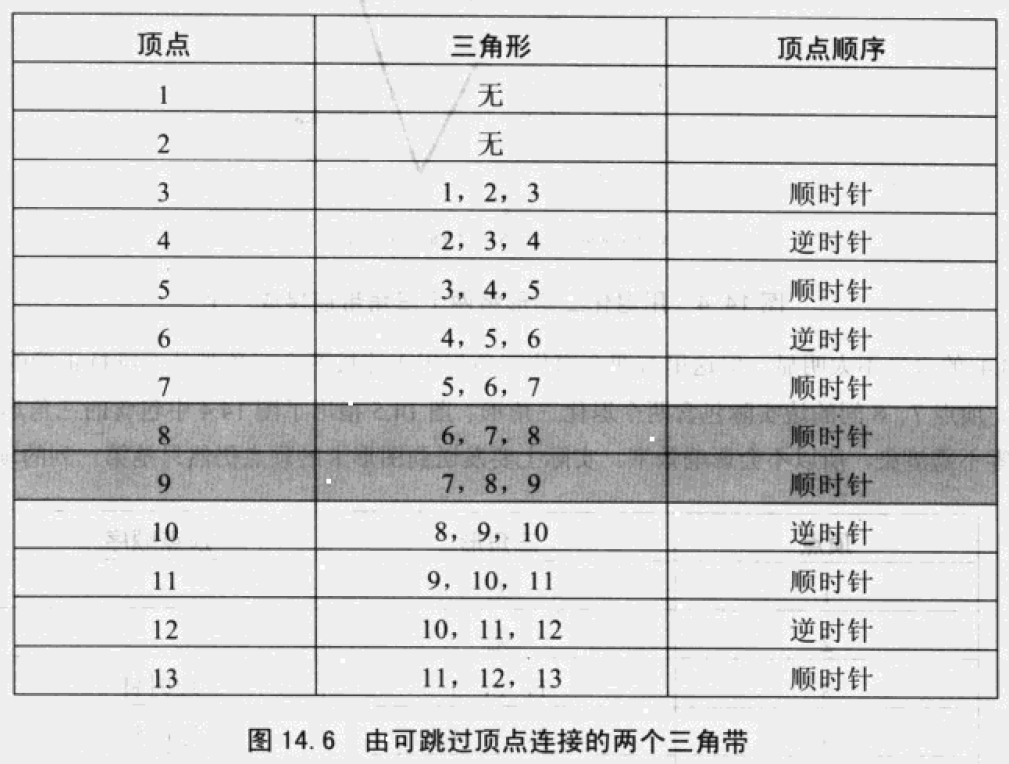
顶点8、9的三角形被置位为“不必绘制”。
三角扇
三角扇和三角带类似,但不如三角带灵活,所以很少使用。
三角扇使用n+2个顶点存储n个面,和三角带相同。但是,第一个顶点必须为所有三角形共享,所以实践中不太经常能找到大型三角扇应用的场合。并且,三角扇不能象三角带那样连接。所以,三角扇只能在特殊场合应用,对一般应用来说,三角带更灵活。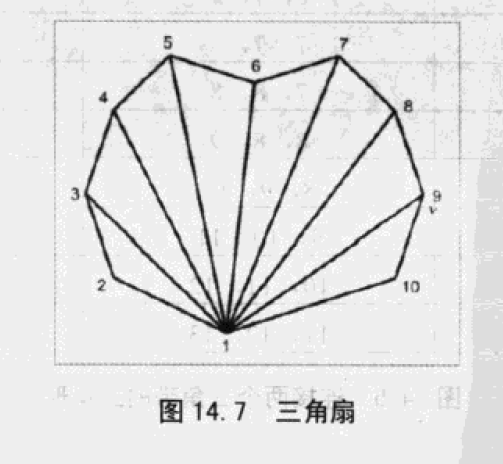
二、额外信息
1、纹理映射坐标
纹理映射是将位图(称作“纹理图”或简称“纹理”)贴到多边形表面的过程。
对多边形中每个需要渲染的像素都要计算2D级理映射坐标,这些坐标用以索引纹理图,从而为相应像素着色。
通常,在顶点保存纹理映射坐标,三角形面中其余各点的坐标通过插值进行计算。
2、表面法向量
在实际应用中,网格上的点都需要一个表面法向量,作用是:
- 计算光照
- 进行背面剔除
- 模拟粒子在表面弹跳效果
- 通过只考虑正面而加速碰撞检测
3、光照值
常由定点维护,常用于沿表面的插值,如Gourand着色(逐顶点计算光照)

