一、字典Dictionary

ADT

  1. template<class Key, class Elem, class KEComp, class EEComp>
  2. class Dictionary{
  3. public:
  4.     virtual void clear() = 0;    //重新初始化
  5.     virtual bool insert(const Elem&) = 0;            //插入一个元素
  6.     virtual bool remove(const Key&, Elem&) = 0;        //根据key删除元素
  8.     //按照自定义规则删除一个元素，循环执行则最终会清空字典。
  9.     virtual bool removeAny(Elem&) = 0;                
  11.     virtual bool find(const Key&, Elem&) const = 0;    //根据key查找元素
  12.     virtual int size() = 0;                            //元素总个数
  13. }

1、字典（无序顺序表）

  1. template<class Key, class Elem, class KEComp, class KKComp>
  2. class UALdict : public Dictionary<Key, Elem, KEComp, KKComp>{
  3. private:
  4.     AList<Elem>* list;
  5. public:
  6.     UALdict(int size = DefaultListSize){
  7.         list = new AList<Elem>(size);
  8.     }
  9.     ~UALdict(){
  10.         delete list;
  11.     }
  12.     void clear(){
  13.         list.clear();
  14.     }
  15.     bool insert(const Elem& elem){
  16.         return list->append(elem);
  17.     }
  18.     bool remove(const Key& key, Elem& elem){
  19.         for(list->setStart(); list->getValue(e); list->next()){
  20.             if(KEComp::eq(K, e)){
  21.                 list->remove(e);
  22.                 return true;
  23.             }
  24.         }
  25.         return false;
  26.     }
  28.     //删除尾部元素
  29.     bool removeAny(Elem& e){
  30.         if(size() == 0) return false;
  31.         list->setEnd();
  32.         list->prev();
  33.         list->remove(e);
  34.         return true;
  35.     }
  36.     bool find(const Key& key, Elem& e){
  37.         for(list->setStart(); list->getValue(e); list->next()){
  38.             if(KEComp::eq(K, e)){
  39.                 return true;
  40.              }
  41.          }
  42.          return false;
  43.     }
  44.     int size(){
  45.         return list->leftLength() + list->rightLength();
  46.     }
  47. }

2、字典（有序顺序表）

  1. template<class Key, class Elem, class KEComp, class KKComp, class EEComp>
  2. class SALdict : public Dictionary<Key, Elem, KEComp, KKComp, EEComp>{
  3. private:
  4.     AList<Elem>* list;
  5. public:
  6.     SALdict(int size = DefaultListSize){
  7.         list = new AList<Elem>(size);
  8.     }
  9.     ~SALdict(){
  10.         delete list;
  11.     }
  12.     void clear(){
  13.         list.clear();
  14.     }
  15.     bool insert(const Elem& elem){
  16.         return list->insert(elem);
  17.     }
  18.     bool remove(const Key& key, Elem& elem){
  19.         for(list->setStart(); list->getValue(e); list->next()){
  20.             if(KEComp::eq(K, e)){
  21.                 list->remove(e);
  22.                 return true;
  23.             }
  24.         }
  25.         return false;
  26.     }
  28.     //删除尾部元素
  29.     bool removeAny(Elem& e){
  30.         if(size() == 0) return false;
  31.         list->setEnd();
  32.         list->prev();
  33.         list->remove(e);
  34.         return true;
  35.     }
  36.     //可以用上面无序一样的，但因为是有序，可以用二分查找
  37.     bool find(const Key& key, Elem& e){
  38.         int l = -1;
  39.         int r = list->leftLength() + list->rightLength();
  40.         while((l + 1) != r){
  41.             int i = (l + r) / 2;
  42.             list->setPos(i);
  43.             list->getValue(e);
  44.             if(KEComp::lt(K, e)) r = i;
  45.             else if(KEComp::eq(K, e)) return true;
  46.             else if(KEComp::lt(K, e)) l = i;
  47.         }
  48.         return false;
  49.     }
  50.     int size(){
  51.         return list->leftLength() + list->rightLength();
  52.     }
  53. }

二、栈Stack

在一端进行插入/删除的线性表，LIFO后进先出。
何必限制一端进行插入删除？
受限制的功能往往意味着更低的实现成本，而这些功能又刚好满足。

ADT

  1. template<class Elem>
  2. class Stack<Elem>{
  3. public:
  4.     virtual void clear() = 0;        //重新初始化
  5.     virtual bool push(const Elem& elem) = 0;    //入栈
  6.     virtual bool pop(Elem& elem) = 0;            //出栈
  7.     virtual bool topValue(Elem& elem) = 0;        //栈顶值
  8.     virtual int length() const = 0;                //当前栈大小
  9. }

1、顺序栈

  1. template<class Elem>
  2. class AStack<Elem> : public Stack<Elem>{
  3. private:
  4.     int size;    //当前栈大小
  5.     int top;    //栈顶位置，0表示栈空
  6.     Elem *listArray;    //栈空间：数组
  7. public:
  8.     AStack(int s = DefaultListSize){
  9.         listArray = new Elem[s];
  10.         size = s;
  11.         top = 0;
  12.     }
  13.     ~AStack(){
  14.         size  = top = 0;
  15.         delete[] listArray;
  16.     }
  17.     void clear(){
  18.         top = 0;
  19.     }
  20.     bool push(const Elem& elem){
  21.         if(top == size) return false;
  22.         listArray[top++] = elem;
  23.         return true;
  24.     }
  25.     bool pop(Elem& elem){
  26.         if(top == 0) return false;
  27.         elem = listArray[--top];
  28.         return true;
  29.     }
  30.     bool topValue(Elem& elem){
  31.         if(top == 0) return false;
  32.         elem = listArray[top-1];
  33.         return true;
  34.     }
  35.     int length() const{
  36.         return top;
  37.     }
  38. }

2、链式栈

  1. template<class Elem>
  2. class LStack : public Stack<Elem>{
  3. private:
  4.     Link<Elem>* top;
  5.     int size;    //当前栈大小
  6. public:
  7.     LStack(int s = DefaultListSize){
  8.         top = NULL;
  9.         size = 0;
  10.     }
  11.     ~LStack(){
  12.         clear();
  13.     }
  14.     void clear(){
  15.         Link<Elem>* temp = NULL;
  16.         while(top != NULL){
  17.             temp = top;
  18.             top = top->next;
  19.             delete temp;
  20.         }
  21.         size = 0;
  22.     }
  23.     bool push(const Elem& elem){
  24.         top = new Link<Elem>(elem, top);
  25.         size++;
  26.         return true;
  27.     }
  28.     bool pop(Elem& elem){
  29.         if(top == NULL) return false;
  30.         elem = top->element;
  31.         top = top->next;
  32.         Link<Elem>* temp = top->next;
  33.         delete top;
  34.         top = temp;
  35.         size --;
  36.         return true;
  37.     }
  38.     bool topValue(Elem& elem){
  39.         if(top == NULL) return false;
  40.         elem = top->element;
  41.         return true;
  42.     }
  43.     int length() const{
  44.         return size;
  45.     }    
  46. }

3、顺序栈和链式栈比较

栈使用率不满时，顺序栈空间浪费。
链式栈有链接域，占空间，压栈入栈有内存分配，频繁的操作性能更低。
顺序栈的有数组的单向延伸性，两个栈，可以考虑一个数组，从两头往中间插入数据。

栈代替递归：汉诺塔

前面汉诺塔的递归算法用栈替换：

  1. enum TOHop { DOMVE, DOTOH };
  3. class TOHobj{
  4. public:
  5.     TOHop op;
  6.     int num;
  7.     Pole start, goal, temp;
  9.     TOHobj(int num, Pole s, Pole g, Pole t){
  10.         op = DOTOH;
  11.         num = num;
  12.         start = s;
  13.         goal = g;
  14.         temp = t;
  15.     }
  16.     TOHobj(Pole s, Pole g){
  17.         op = DOMOVE;
  18.         start = s;
  19.         goal = g;
  20.     }
  21. }
  23. void TOH(int num, Pole start, Pole goal, Pole temp, Stack<TOHobj*>& stack){
  24.     stack.push(TOHobj(num, start, goal, temp));
  25.     TOHobj *t;
  26.     while(stack.pop(t)){
  27.         if(t->op == DOMOVE){
  28.             move(t->start, t->goal);
  29.         }
  30.         else if(t->num > 0){
  31.             int num = t->num;
  32.             Pole temp = t->temp;
  33.             Pole goal = t->goal;
  34.             Pole start = t->start;
  35.             //压栈的顺序和调用顺序是相反的，所以下面三句也应该要反。
  36.             stack.push(new THOobj(num - 1, temp, goal, start));
  37.             stack.push(new THOobj(start, goal));
  38.             stack.push(new THOobj(num - 1, start, temp, goal));
  39.         }
  40.         delete t;
  41.     }
  42. }

三、队列Queue

队尾插入，队首删除的线性表。注意不是队首插入！！！

ADT

  1. template<class Elem>
  2. class Queue{
  3. public:
  4.     virtual void clear() = 0;    //重新初始化
  5.     virtual bool enqueue(const Elem&) = 0;
  6.     virtual bool dequeue(Elem&) = 0;
  7.     virtual bool frontValue(Elem&) const = 0;
  8.     virtual length() const = 0;        //当前队列长度
  9. }

1、（顺序）队列

1、直接用数组的话，入队/出队会引起所有成员移动位置，性能会非常低。
2、队列数据放在数组中间，想法很好，性能很好，但是大小受限。
3、“环形”数组实现，不是数组真的环形，是以在队列位置mod模除队列长度来取数组地址。
4、队列长度n，数组长度必须是n+1，才好区分队列空和满的情况；当然也可以通过计数的方式。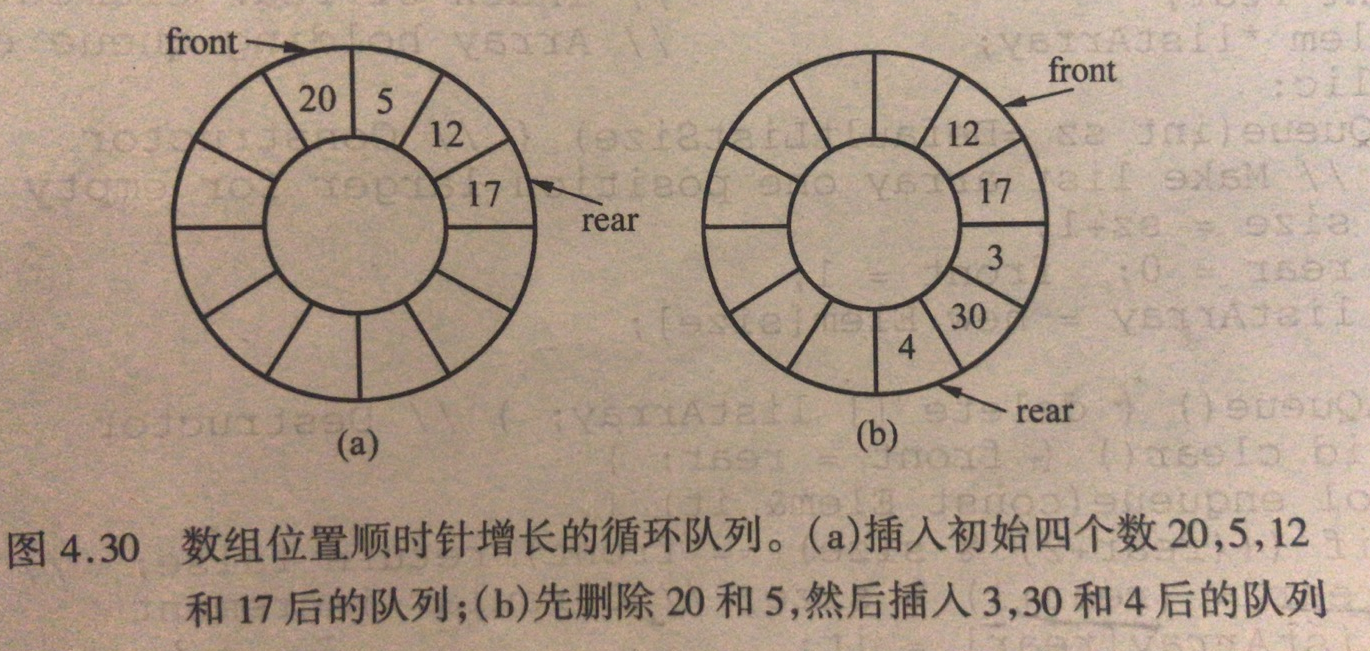
image.png
认真理解上图中文字。

  1. template<class Elem>
  2. class AQueue : public Queue<Elem>{
  3. private:
  4.     int size;        //队列空间大小 + 1
  5.     int front;        //队首
  6.     int rear;        //队尾
  7.     Elem *listArray;    //队列空间
  8. public:
  9.     AQueue(int size = DefaultListSize){
  10.         this->size = size + 1;
  11.         front = 1;    //第一个元素从位置1开始插入
  12.         rear = 0;
  13.         listArray = new Elem[size + 1];
  14.     }
  15.     ~AQueue(){
  16.         delete[] listArray;
  17.     }
  18.     void clear(){
  19.         front = rear;
  20.     }
  21.     bool enqueue(const Elem& elem){
  22.         if ((rear + 2) % size == front) return false;
  23.         rear = (rear + 1) % size;
  24.         listArray[rear] = elem;
  25.         return true;
  26.     }
  27.     bool dequeue(Elem& elem){
  28.         if(length() == 0) return false;
  29.         elem = listArray[front];
  30.         front = (front + 1) % size;
  31.         return true;
  32.     }
  33.     bool frontValue(Elem& elem) const{
  34.         if(length() == 0) return false;
  35.         elem = listArray[front];
  36.         return true;
  37.     }
  38.     virtual int length() const{
  39.         return ((rear + size) - front + 1) % size;
  40.     }
  41. }

2、（链式）队列

  1. template<class Elem>
  2. class LQueue : public Queue<Elem>{
  3. private:
  4.     Link<Elem> *front;    //队首
  5.     Link<Elem> *rear;    //队尾
  6.     int size;    //当前队列长度
  7. public:
  8.     LQueue(int size = DefaultListSize){
  9.         front = NULL;
  10.         rear = NULL;
  11.         size = 0;
  12.     }
  13.     ~LQueue(){
  14.         clear();
  15.     }
  16.     void clear(){
  17.         Link<Elem> *temp = NULL;
  18.         while(front != NULL){
  19.             rear = front;
  20.             front = front->next;
  21.             delete rear;
  22.         }
  23.         rear = NULL;
  24.         size = 0;
  25.     }
  26.     bool enqueue(const Elem& elem){
  27.         if(size == 0){
  28.             front = rear = new Link<Elem>(elem, NULL);
  29.         }
  30.         else{
  31.             rear->next = new Link<Elem>(elem, NULL);
  32.             rear = rear->next;
  33.         }
  34.         size++;
  35.         return true;
  36.     }
  37.     bool dequeue(Elem& elem) const {
  38.         if(size == 0) return false;
  39.         elem = front->element;
  40.         Link<Elem>* temp = front;
  41.         front = front->next;
  42.         if(front == NULL) rear = NULL;
  43.         delete temp;
  44.         size --;
  45.         return true;
  46.     }
  47.     bool frontValue(Elem& elem) const {
  48.         if(size == 0) return false;
  49.         elem = front->element;
  50.         return true;
  51.     }
  52.     int length() const{
  53.         return size;
  54.     }
  55. }