OpenGL其中的一个主要工作是将3D坐标转化为屏幕上的2D像素坐标（离散的）。期间进行复杂的矩阵变换，OpenGL将这个复杂的过程分成几个子过程，每个过程完成特定的计算工作。

OpenGL_坐标变换（Transform） - 图1

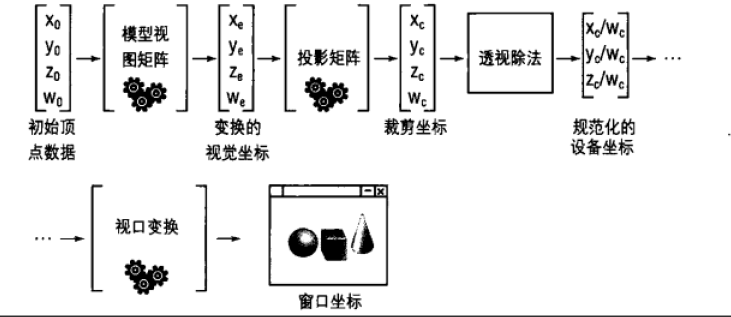
对应代码如下：


// ************************************************
// ************ 顶 点 着 色 器
// ************************************************
#version 330 core
layout(location = 0) in vec3 pos;        // 顶点局部坐标(在模型中的坐标)
uniform mat4 modelMatrix;                // 模型矩阵
uniform mat4 viewMatrix;                // 视图矩阵
uniform mat4 projectionMatrix;            // 投影矩阵
void main()
{
    vec3  localPos = pos;                // 局部空间（模型空间）坐标
    float w           = 1.0;                   // w分量（x、y、z、w）
    vec4  posVec4  = vec4(localPos, w);    // 转换成4D齐次坐标（用4D向量表示3D坐标）
    vec4  posInWorld  = modelMatrix      * posVec4;            // 模型矩阵变换，得到世界坐标
    vec4  posInCamera = viewMatrix       * posInWorld;        // 视图矩阵变换，得到视图坐标
    vec4  clippingPos = projectionMatrix * posInCamera;        // 投影矩阵变换，得到裁剪坐标
    gl_Position = clippingPos;            // 顶点着色器输出裁剪坐标，用于后续高效裁剪。
}

我们对上面代码中的每一步都进行见详细的解释。

一、局部空间

#version 330 core
layout(location = 0) in vec3 pos;        // 顶点局部坐标(在模型中的坐标)
......
void main()
{
    vec3  localPos = pos;                // 局部空间坐标
    ......
}

就是指物体本地坐标系，也可以叫模型空间。
这个坐标系由模型设计者定义，比如我们使用建模软件（比如Blender）创建一个立方体模型。最简单的情况，我们在建模的时候可以定义坐标系的原点在立方体中心位置，坐标轴分别垂直立方体的两个面，则：


// 立方体的8个顶点的坐标分别是：
//        0.5, -0.5,  0.5    右下角-前
//        0.5,  0.5,  0.5    右上角-前
//       -0.5,  0.5,  0.5    左上角-前
//        -0.5, -0.5,  0.5    左下角-前
//         0.5, -0.5, -0.5    右下角-后
//         0.5,  0.5, -0.5    右上角-后
//        -0.5,  0.5, -0.5    左上角-后
//        -0.5, -0.5, -0.5    左下角-后

二、4D齐次坐标与齐次矩阵

#version 330 core
layout(location = 0) in vec3 pos;        // 顶点局部坐标(在模型中的坐标)
......
void main()
{
    float w          = 1.0;                // w分量（x、y、z、w）
    vec4  posVec4 = vec4(localPos, w);    // 转换成4D齐次坐标（用4D向量表示3D坐标）
    ......
}

将3D坐标转换成4D齐次坐标表示，目的是为了能使用4x4齐次矩阵进行平移变换（沿x、y、z轴方向移动）。
w = 1.0时，表示平移变换生效。
w = 0.0时，将没有平移变换效果，4x4齐次矩阵的变换效果就等同于它左上角3x3矩阵部分的线性变换。
这有什么意义？比如单位法向量只关注方向，无需考虑位置，所以单位法向量的变换无需考虑平移，可以令w=0.0。

三、模型矩阵变换（Model Matrix）

顶点在世界坐标系中的变换（旋转、缩放、平移等），顶点初始位置在世界坐标系原点。


// modelMatrix:    模型矩阵
// posVec4:        4D齐次坐标
// posInWorld:    世界坐标（其实就是所有模型的顶点都在同一个坐标系中）
vec4 posInWorld = modelMatrix * posVec4;        // 模型矩阵变换

将所有模型各自模型空间下的局部坐标统一变换到ModelMatrix定义的坐标系中（世界坐标系）。
模型的初始位置：模型的局部坐标系的原点在世界坐标系的原点位置。
右乘ModelMatrix矩阵，相当于模型在世界坐标系中进行各种变换：

平移变换：移动模型到指定位置
缩放变换：放大或者缩小模型
旋转变换：绕任意轴旋转任意角度
镜像变换：把模型变成镜子里的镜像（左手和右手调换了）
。。变换

总结这一步的工作就是，将模型全部放好位置。

下面代码是如何构建模型矩阵：


glm::mat4 modelMatrix( 1.0f );      // 注意，必须初始化为单位矩阵，而不是零矩阵
// 平移效果
modelMatrix = glm::translate( modelMatrix, glm::vec3(5.0f,        // 在x方向的位移
                                                     6.0f,        // 在y方向的位移
                                                     7.0f ) );    // 在z方向的位移
// 旋转效果
modelMatrix = glm::rotate( modelMatrix,
                          glm::radians( 90.0f ),            // 旋转90°
                          glm::vec3(0.0f, 1.0f, 0.0f ) );    // 绕的旋转轴
// 缩放效果
modelMatrix = glm::scale( modelMatrix,
                         glm::vec3( 0.5f, 0.6f, 0.7f ) );    // 分辨在xyz方向上的缩放因子
// 最终得到的矩阵的变换效果就是：先平移，再旋转，最后缩放变换。注意顺序不能变动。

四、视图矩阵变换（View Matrix）


// viewMatrix:        视图矩阵
// posInWorld:        世界坐标
// posInCamera:        摄像机坐标系中的坐标
vec4  posInCamera = viewMatrix * posInWorld;
// 将世界坐标全部变换到viewMatrix定义的坐标系中（摄像机坐标系）。
// 通俗理解就是直播摄影师肩扛着摄像机，找了一个位置拍这些放好的模型。而我们通过屏幕实时观看了拍摄画面。

将世界坐标转换到ViewMatrix定义的坐标系中（摄像机坐标系）。
摄像机坐标系定义如下：

原点：摄像机位置。
轴正方向：摄像机的“正右方”方向。
Y轴正方向：摄像机的“正上方”方向。
Z轴正方向：摄像机的“正后方”方向。

总结这一步的工作，就是确定观察角度。

顺便说一句，在第一人称视角游戏中，我们的视角是不断变化的，因此这个视图矩阵也是不断在改变的。

下面代码是如何构建视图矩阵：


// 待完成

五、投影矩阵变换（Projection Matrix）


// projectionMatrix:    投影矩阵
// posInCamera:            摄像机坐标系中的顶点坐标
// clipPos:                裁剪坐标，叫裁剪坐标的原因是，这个坐标非常容易判断是否需要被裁剪。
vec4  clipPos = projectionMatrix * posInCamera;
// 裁剪坐标，特征如下：
// 令，clipPos = (x, y, z, w)，若满足以下三个条件，
// 则clipPos在projectionMatrix定义的视景体（View Volume）内部：
// 1、-w <= x <= w
// 2、-w <= y <= w
// 3、-w <= z <= w
// 还要一个重要特性，随着posInCamera.z值的线性增长，clipPos.z的值并不是线性增长，而是增长的越来越慢，比如：
// posInCamera.z从0   -> 10 时，clipPos.z从0.0w -> 0.5w。
// posInCamera.z从10  -> 100时，clipPos.z从0.5w -> 1.0w。
// 这就是深度值的非线性特性，目的是让近景的物体的深度有更高精度。

下面代码是如何构建投影矩阵：


glm::mat4 projection(1.0f);
// *********************************
// ******* 正 交 投 影 矩 阵
// *********************************
// 正交投影并没有远近的概念，远的东西和近的东西大小都是一样的
// 换句话说，所有的顶点的Z值都相同，正交投影的视景体就是一个矩形
projection = glm::ortho(0.0f, 0.0f,            // 视景体的左下角位置
                        800.0f, 600.0f);    // 视景体的右上角位置
// *********************************
// ******* 透 视 投 影 矩 阵
// *********************************
// 透视投影的视景体是一个平截头体（Frustum），削了顶的金字塔形状。
// 有6个面（plane）：远近、上下、左右。
projection = glm::perspective( 
    glm::radians( pCamera->fov() ),            // 就是FOV，field of view，视角广度
    ( float ) ScreenWidth / ScreenHeight,      // aspectRatio，宽高比
    0.1f,                                      // near plane，近平面位置，离摄像头更近的那一面
    100.0f );                                  // far plane，远平面位置

六、透视除法（Perspective Divde）

图形硬件会自动完成。
将裁剪坐标转化成标准设备空间坐标（Normalized Device Coordinate, NDC），即x、y、z分量都在[ -1.0, 1.0 ]之间。做法很简单。
OpenGL_坐标变换（Transform） - 图3
当为正交投影时， OpenGL_坐标变换（Transform） - 图4 。
当为透视投影时，顶点坐标离观察点越远， OpenGL_坐标变换（Transform） - 图5 分量越大，相同的距离映射到屏幕上的距离就会越小，这就是实现透视效果（近大远小）的原理。

七、视口变换（Viewport Transform）

图形硬件会自动完成。
接下来我们需要将NDC坐标映射到一个指定大小的矩形显示区域（视口）中。比如视口大小刚好是窗口大小，则相当于把NDC坐标转换成屏幕坐标。


GLsizei ScreenWidth  = 800;    // 屏幕宽高
GLsizei ScreenHeight = 600;
glViewport( 0, 0,                           // 视口左下角在窗口中的坐标
            ScreenWidth, ScreenHeight );    // 视口宽高
// 将NDC坐标映射到800x600的屏幕上的屏幕坐标。

最后变换出来的屏幕坐标将会送到光栅器，将其转化为片段。

八、矩阵相关

矩阵根据内部元素的排序规则分两种类型：

列优先（Column Major）
行优先（Row Major）

OpenGL_坐标变换（Transform） - 图6

OpenGL采用列优先的矩阵，主要原因是OpenGL想用一维数组来构造矩阵，而不是二维数组（速度更慢），C中的二维数组是行优先规则。
因此向量也都是列向量形式。根据线性代数规则，应该是 OpenGL_坐标变换（Transform） - 图7 ，而不能 OpenGL_坐标变换（Transform） - 图8 。

模型视图变换矩阵

根据线性代数矩阵特性，我们可以讲模型矩阵和视图矩阵相乘得到模型视图变换矩阵，它其实就是先执行模型变换再执行视图变换的效果。
点击查看【processon】