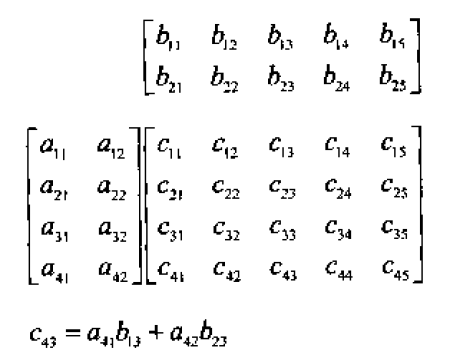示例项目
https://github.com/JackieLong/OpenGL/tree/main/project_matrix_transform

一、数学定义

向量定义为一维数组，矩阵定义为二维数组。
向量是标量的数组，矩阵是向量的数组。
矩阵的维度定义为矩阵包含多少行和多少列，如下是一个矩阵。

注意矩阵的下标从1开始，数组是从0开始，不用数组表达矩阵的原因之一。

二、方阵

“四四方方”的矩阵，行列数相等。

1、对角矩阵

所有非对角线元素都为0。
对角线元素就是行号和列号相同的元素，其他为非对角线元素。

2、单位矩阵

矩阵的单位矩阵犹如标量的1，

3、向量也是矩阵

三、矩阵转置

四、矩阵乘法

• 解释
  • 
• 助记

1、2x2矩阵乘法

2、3x3矩阵乘法

3、注意事项

任意矩阵M乘以方阵S，不管从哪边乘，都将得到与原矩阵大小相同的矩阵。当然，前提是假定乘法有意义。
。

（设乘法有意义）

五、向量与矩阵乘法

向量就是行矩阵或列矩阵。

行向量左乘矩阵有意义，得行向量。

列向量右乘矩阵有意义，得列向量

其他情况，无意义。

1、行向量？还是列向量

到底是用行向量？还是列向量？
首先行向量，列向量的乘法是完全不同的，在不同的场合，使用的向量有不同。

• 使用行向量
  • 书写形式更好
  • 左乘形式，更方便，对于矩阵乘法实现坐标系转换。如用矩阵A、B、C转换向量C，用行向量记为，用列向量则要记为
  • DirectX中使用行向量。
• 使用列向量
  • OpenGL
  • 大多数线性代数书籍
  • 多本计算机图形学“圣经”

使用第三方的公式和源码时，必须要先确定使用的是行向量还是列向量。

2、几何意义

![](https://cdn.nlark.com/yuque/__latex/ad382bc82567318c14e23bf066cd0b4f.svg#card=math&code=%5CLarge%20%5Cbegin%7Baligned%7D%0A%5Cmathbf%7Bv%7D%20%26%3D%5Cbegin%7Bbmatrix%7Dx%0A%20%5C%5Cy%0A%20%5C%5Cz%0A%0A%5Cend%7Bbmatrix%7D%3D%5Cbegin%7Bbmatrix%7Dx%0A%20%5C%5C0%0A%20%5C%5C0%0A%0A%5Cend%7Bbmatrix%7D%2B%5Cbegin%7Bbmatrix%7D0%0A%20%5C%5Cy%0A%20%5C%5C0%0A%0A%5Cend%7Bbmatrix%7D%2B%5Cbegin%7Bbmatrix%7D0%0A%20%5C%5C0%0A%20%5C%5Cz%0A%0A%5Cend%7Bbmatrix%7D%3Dx%5Cbegin%7Bbmatrix%7D1%0A%20%5C%5C0%0A%20%5C%5C0%0A%0A%5Cend%7Bbmatrix%7D%2By%5Cbegin%7Bbmatrix%7D0%0A%20%5C%5C1%0A%20%5C%5C0%0A%0A%5Cend%7Bbmatrix%7D%2Bz%5Cbegin%7Bbmatrix%7D0%0A%20%5C%5C0%0A%20%5C%5C1%0A%0A%5Cend%7Bbmatrix%7D%0A%5C%5C%5Cnewline%0A%26%3Dxp%2Byq%2Bzr%EF%BC%8Cp%E3%80%81q%E3%80%81r%E4%B8%BAx%E3%80%81y%E3%80%81z%E8%BD%B4%E7%9A%84%E5%8D%95%E4%BD%8D%E5%90%91%E9%87%8F%E3%80%82%0A%5Cend%7Baligned%7D&height=154&width=638)    

向量表示成了的线性变换，事实上可以任意的3D笛卡尔坐标轴的单位向量，这里已经暗示了坐标转换。

以构建矩阵，则有：

如果把矩阵的行解释为坐标系的基向量，那么乘以该矩阵就相当于执行了一次坐标转换，若有。如果矩阵不是基向量组成，其实也可以转换成标量乘以基向量，这个标量就相当于在该向量方向的缩放倍数。
从上面我们可以看出，矩阵不过是一种紧凑的方式来表达坐标转换所需的数学运算。

假设矩阵，从矩阵抽出基向量，。则M代表的是逆时针旋转26°。
点击查看【processon】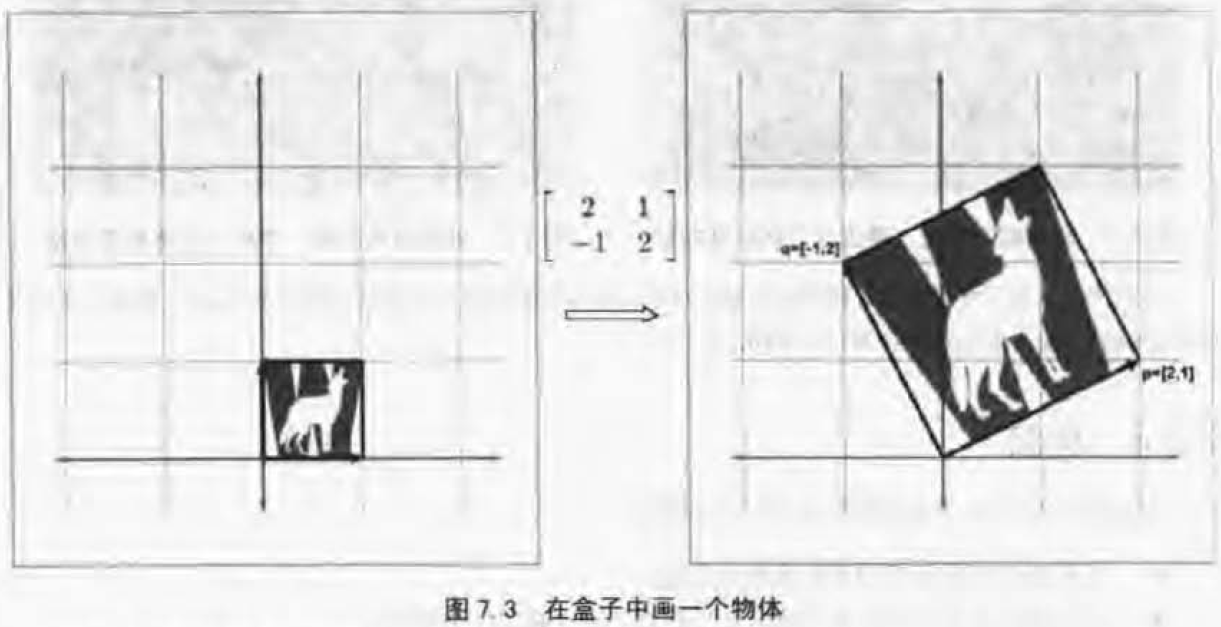

从上图可以看出，矩阵不仅旋转坐标，还会拉伸它。
扩展到3D转换中，2D中有两个基向量，构成“L”型，3D中有三个基向量，构成“三脚架”。

3、总结

方阵的行被解释为坐标系的基向量。

为了将向量从原坐标系转换到新坐标系，用它乘以一个。

从原坐标系到这些基向量定义的新坐标系的变换是一个线性变换，线性变换保持直线和平行线，但角度、长度、面积、体积会发生改变。

零向量乘以任何矩阵都等于零向量，因此，方阵代表的线性变换的原点和原坐标系的原点一致，意味着无法实现平移变换。

可以通过想象变换后的坐标系的基向量来想象矩阵，这些基向量在2D中构成“L”型，在3D中构成“三脚架”型。

六、矩阵的行列式

只有方阵有行列式，非方阵的行列式是未定义的。阶矩阵的行列式复杂度随n的增长成指数增长。

1、2阶方阵行列式

注意，用的是竖线，不是矩阵的方括号。结果是标量，不是矩阵。

2、3阶方阵行列式

助记

把
用+号对角线上的元素积减去-号对角线上的元素积

3、余子式

4、代数余子式

相应余子式的有符号行列式.，结果是一个标量。

通过代数余子式来计算矩阵行列式。

下面是阶行列式的计算过程：

代数余子式矩阵

所有的余子式对应的代数余子式组成的矩阵。
，计算的代数余子式矩阵如下：

5、行列式性质

积的行列式=行列式的积

矩阵转置的行列式=原矩阵的行列式

如果矩阵的任意行/列为零，则行列式为零。

交换矩阵的任意两行/列，行列式变负

任意行/列的非零积加到另一行/列上不会改变行列式的值。

6、行列式几何意义

2D几何意义

行列式等于以基向量为两边的平行四边形的有符号面积。有符号指的是如果平行四边相对于原来的方位翻转，那么面积变负。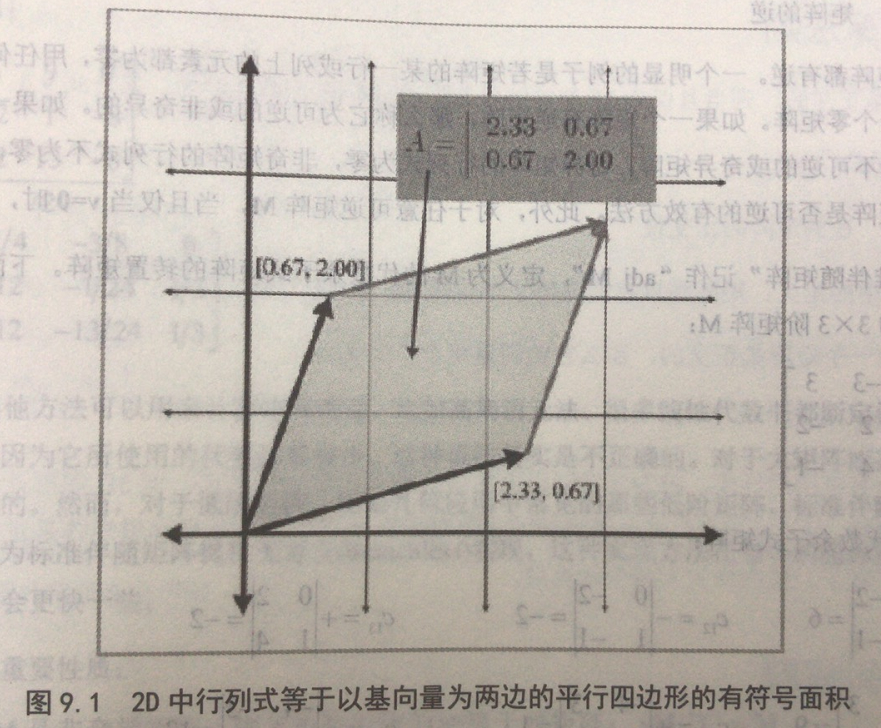

3D几何意义

行列式等于以变换后的基向量为三边的平行六面体的有符号体积，如果变换使得平行六面体“由里向外”翻转，则行列式变负。
行列式与它相关：矩阵变换导致的尺寸改变。
行列式的绝对值和它相关：面积（2D）、体积（3D）。
行列式的符号说明了变换矩阵是否包含镜像、投影。
行列式为零，则矩阵包含投影。
行列式为负，则矩阵包含镜像。

七、矩阵的逆

只能用于方阵。

可以类比倒数。分母不能为0，在矩阵中对应的就是某一行/列不能为0，因为任何矩阵乘以该矩阵结果都是一个零矩阵。所以并非所有的矩阵都是可逆的。

• 可逆矩阵
  • 有逆矩阵
  • 行列式≠0
• 不可逆矩阵（奇异矩阵）
  • 没有逆矩阵
  • 行列式=0**

    1、计算方法：标准伴随矩阵

    
    

接着上面的代数余子式矩阵例子，计算M的“标准伴随矩阵”：

接着上面的例子。

还有一种方法叫做，高斯消元法，适合大矩阵和某些特殊矩阵。

2、矩阵逆性质

若M不是奇异矩阵，则

单位矩阵的逆是它本身。

转置的逆等于逆的转置。

矩阵乘积的逆等于矩阵的逆的相反顺序的乘积。

3、几何意义

矩阵的逆非常有用，可以计算变换的“方向”或“相反”变换（能撤销原变换的变换）。很容易通过代数方法验证：

八、正交矩阵

若方阵是正交的，当且仅当与的乘积等于单位矩阵。

如果矩阵是正交的，矩阵的转置就是矩阵的逆，可以避免计算逆矩阵的代价。

1、几何意义

如何检测是否是正交矩阵？

，

上面9个等式可转化为：

当且仅当是单位向量时，它与它自身的点积结果是1，因此
当且仅当两个向量互相垂直时，点击为零，因此

综上若一个矩阵是正交矩阵，则必须满足以下条件：

• 矩阵每一行必须是单位向量
• 矩阵所有行必须互相垂直

注意，仅在预先知道是正交矩阵的情况下才能利用正交性的特点，如果预先不知道，那么检查正交性完全是浪费时间。

如果一组向量互相垂直，这组向量被认为是正交基（orthogonal basis），如果这组向量还是单位向量，则称它们为标准正交基（orthonormal basis），正交矩阵的行/列向量都是标准正交基向量。

2、正交化（施密特正交化）

有时可能会遇到略微违反了正交性的矩阵。例如，可能从外部得到了坏数据，或者是浮点数运算的累积错误（“矩阵爬行”）。这些情况下，需耍做矩阵正交化，得到一个正交矩阵，这个矩阵要尽可能地和原矩阵相同（至少希望是这样）。