1、概念

节点叫顶点vertex，顶点之间的连线叫边edge。
树、线性表是形式受限的图。
图是数据结构的最通用的形式。
G = ( V, E )，V是顶点集合，E是边集合。
|V|，|E|：顶点数、边数。
|E|：0 ~ O( |V| )。
包含所有可能的边，叫完全图。
有向图、无向图、标号图、带权图。
路径path，路径长度length = 边数。
简单路径：路径顶点各不相同。
回路：路径首尾是同一个节点，路径长度>=3。
密集图：边数较多的图。
稀疏图：边数较少的图。
简单回路：简单路径的回路。全部概念如下图：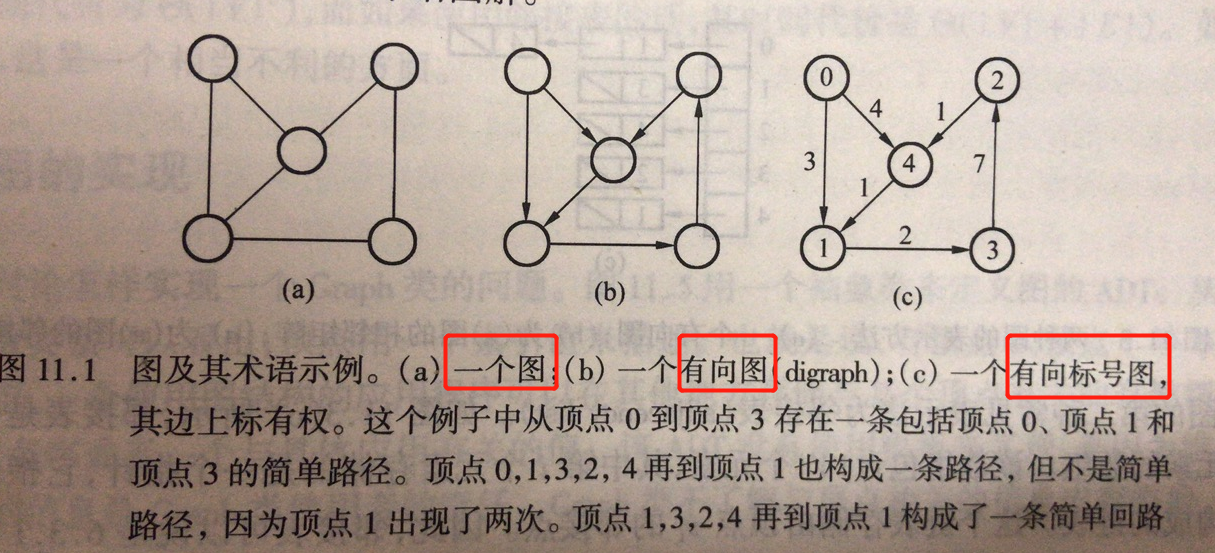
image.png
连通的无向图：每个顶点到任意其他顶点都有路径。
连通分量：无向图的最大连通子图。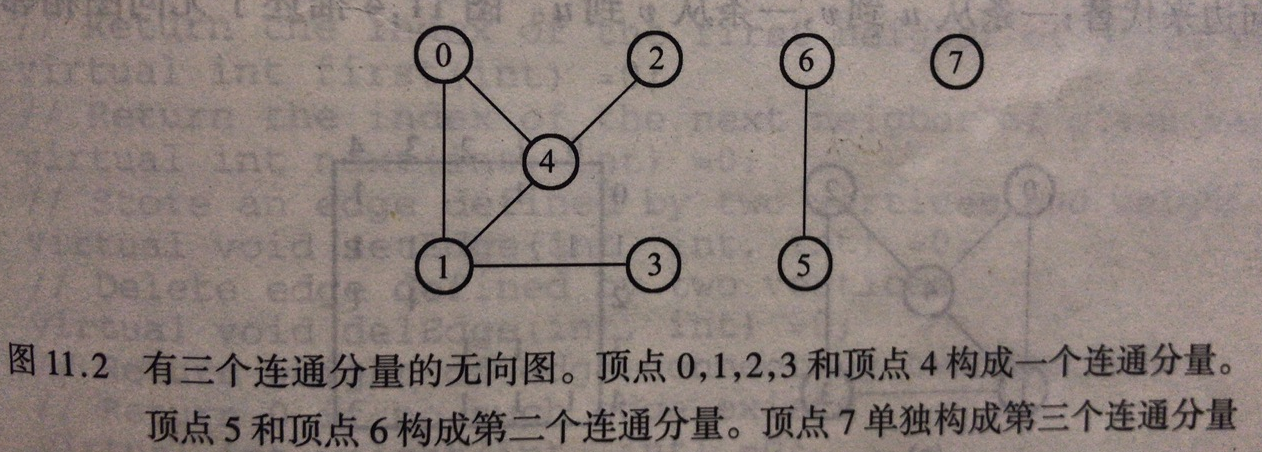
image.png
（有向）无环图：不带回路的（有向）图。
自由树：不带简单回路的连通无向图。连通且有|V| - 1条边的图。

2、图的表示方法

相邻矩阵：两个顶点边的权值，没有边返回0，所以!0表示顶点间有边相连。
领接表：链表存储边（Edge），边存储指向下一个的顶点和边权值。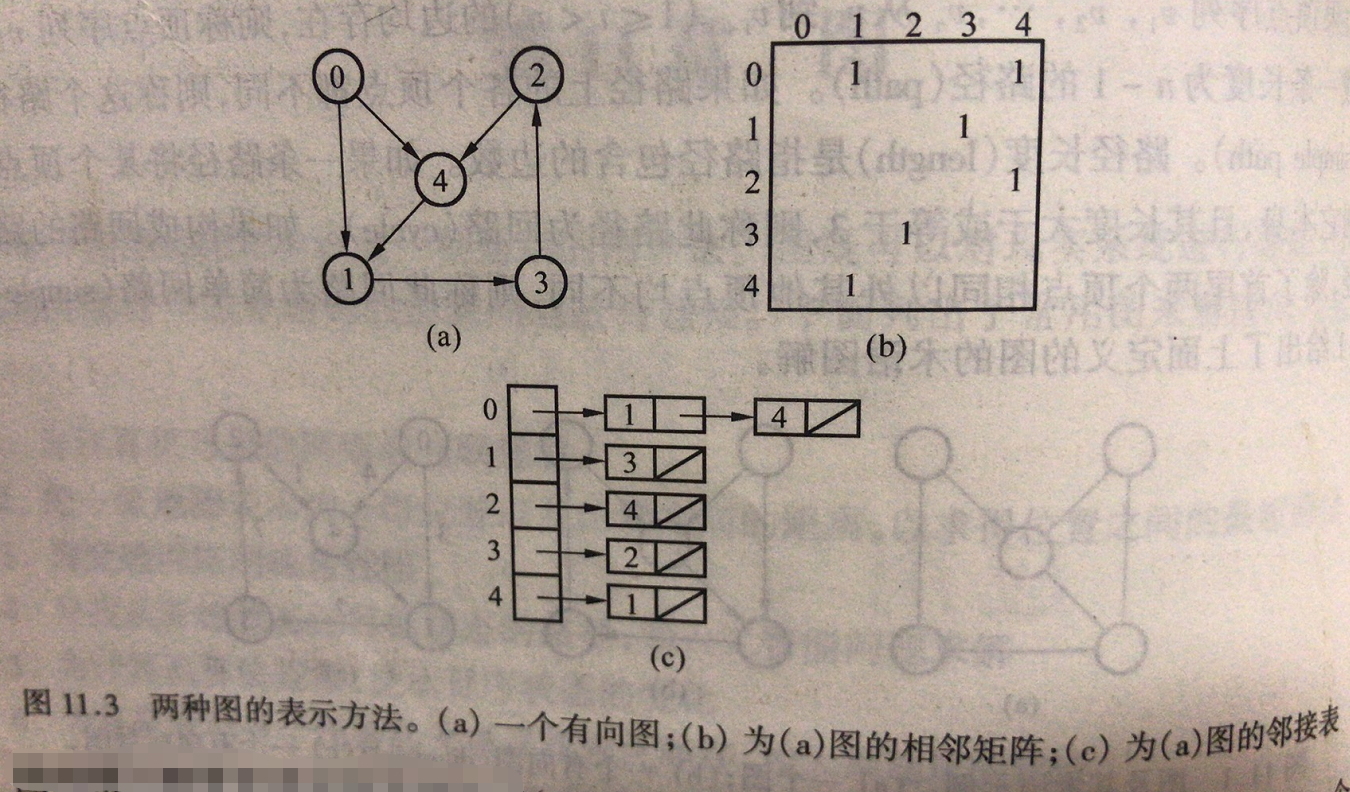
image.png

3、图ADT（抽象基类）

  1. class Graph{
  2. public:
  3.     virtual int n() = 0;    //顶点数
  4.     virtual int e() = 0;    //边数
  5.     virtual int first(int v) = 0;        //顶点v相邻第一个邻居顶点
  6.     virtual int next(int v, int v_n) = 0;    //返回顶点v的下一相连顶点
  7.                                             //比如0-1-2-3-4-5：顶点都相连
  8.                                             //next(0, 3) = 4;
  9.                                             //next(0, 5) = 6;即到达尾部，返回顶点数。
  10.     virtual void setEdge(int v1, int v2, int weight) = 0;    //存储边（顶点v1、v2，权重weight）
  11.                                                             //可以以此创建图
  12.     virtual void delEdge(int v1, int v2) = 0;        //删除边(v1, v2)
  13.     virtual int weight(int v1, int v2) = 0;            //边(v1, v2)的权重，如果不存在返回0
  14.     virtual int getMark(int v1) = 0;                //返回v1的标号值
  15.     virtual void setMark(int v1, int value) = 0;    //设置顶点v1的标号值
  16. }

图的实现（矩阵）

  1. //边edge的类
  2. //为什么只存储了一点顶点和权重？
  3. //因为这些信息已经足够遍历图了。想象一下，初始提供一个顶点。
  4. class Edge{
  5. public:
  6.     //vertex：表示指向的顶点。
  7.     //weight：表示与vertex相连边的权重
  8.     int vertex, weight;
  9.     Edge(){ vertex = -1; weight = -1; }
  10.     Edge(int v, int w){ vertex = v; weight = w; }
  11. }
  13. class GraphMatrix : public Graph{
  14. private:
  15.     int     numVertex, numEdge;    //顶点数，边数
  16.     int**     matrix;        //矩阵数组：下标值为顶点索引，值为权重
  17.     int*    mark;        //顶点标记，是否访问过
  18. //函数接口声明
  19. public:
  20.     GraphMatrix(int numVert);
  21.     ~GraphMatrix();
  22.     int n();
  23.     int e();
  24.     int first(int v);
  25.     int next(int v1, int v2);
  26.     void setEdge(int v1, int v2, int wgt);
  27.     void delEdge(int v1, int v2);
  28.     int weight(int v1, int v2);
  29.     int getMark(int v);
  30.     void setMark(int v, int val);
  31. //函数定义
  32. public:
  33.     GraphMatrix(int numVert){
  34.         int i, j;
  35.         numVertex = numVert;
  36.         numEdge = 0;
  37.         mark = new int[numVert];
  38.         for(i = 0; i < numVertex; i++) mark[i] = UNVISITED;
  39.            maxtrix = (int**)new int*[numVertex];
  40.         for(i = 0; i < numVertex; i++) *(maxtrix+i) = new int[numVert];
  41.         for(i = 0;i < numVertex; i++)
  42.             for(int j = 0;j < numVertex;j++)
  43.                 matrix[i][j] = 0;
  44.     }
  45.     ~GraphMatrix(){
  46.         delete[] mark;
  47.         for(int i = 0;i < numVertex; i++) delete[] matrix[i];
  48.         delete[] maxtrix;
  49.     }
  50.     int n(){ return numVertex; }
  51.     int e(){ return numEdge; }
  52.     int first(int v){
  53.         int i;
  54.         for(i = 0;i < numVertex; i++) if(matrixp[v][i] != 0) return i;
  55.         return i;
  56.     }
  57.     int next(int v1, int v2){
  58.         int i;
  59.         for(i = v2 + 1;i < numVertex; i++) if(matrix[v1][i] != 0) return i;
  60.         return i;
  61.     }
  62.     void setEdge(int v1, int v2, int wgt){
  63.         Assert(wgt > 0, "Illegal weight value.");
  64.         if(matrix[v1][v2] == 0) numEdge++;
  65.         matrix[v1][v2] = wgt;
  66.     }
  67.     void delEdge(int v1, int v2){
  68.         if(matrix[v1][v2] != 0) numEdge--;
  69.         matrix[v1][v2] = 0;
  70.     }
  71.     int weight(int v1, int v2){ return matrix[v1][v2]; }
  72.     int getMark(int v){ return mark[v]; }
  73.     void setMark(int v, int val){ mark[v] = val; }
  74. }

图的实现（邻接表）

  1. class GraphLink : public Graph{
  2. private:
  3.     int numVertex, numEdge;
  4.     List<Edge>** vertex;    //注意，下标是顶点索引，链表项是与它相连的边。
  5.     int *mark;        //顶点标记，是否访问过
  6. public:
  7.     GraphLink(int numVert){
  8.         int i, j;
  9.         numVertex = numVert;
  10.         numEdge = 0;
  11.         mark = new int[numVert];
  12.         for(i = 0; i < numVertex; i++) mark[i] = UNVISITED;
  13.         vertex = (List<Edge>**) new List<Edge>*[numVertex];
  14.         for(i = 0; i < numVertex; i++)
  15.             vertex[i] = new LList<Edge>();
  16.     }
  17.     ~GraphLink(){
  18.         delete[] mark;
  19.         for(int i = 0;i < numVertex; i++) delete[] vertex[i];
  20.         delete[] vertex;
  21.     }
  22.     int n(){ return numVertex; }
  23.     int e(){ return numEdge; }
  24.     int first(int v){    //也就是第一条边指向的顶点
  25.         Edge it;
  26.         vertext[v]->setStart();
  27.         if(vertext[v]->getValue(it)) return it.vertex;
  28.         else return numVertex;
  29.     }
  30.     int next(int v1, int v2){
  31.         Edge it;
  32.         vertex[v1]->getValue(it);
  33.         if(it.vertex == v2) vertex[v1]->next();
  34.         else{
  35.             //循环直到找到v2顶点
  36.             vertex[v1]->setStart();
  37.             while(vertext[v1]->getValue(it) && (it.vertex <= v2))
  38.                 vertex[v1]->next();
  39.         }
  40.         if(vertex[v1]->getValue(it)) return it.vertex;
  41.         else return numVertex;
  42.     }
  43.     void setEdge(int v1, int v2, int wgt){
  44.         Assert(wgt > 0, "Illegal weight value.");
  45.         Edge it(v2, wgt);
  46.         Edge curr;
  47.         vertex[v1]->getValue(curr);
  48.         if(curr.vertex != v2){
  49.             //循环直到找到顶点v2
  50.             for(vertex[v1]->setStart(); vertex[v1]->getValue(curr);vertex[v1]->next())
  51.                 if(curr.vertex >= v2) break;
  52.         }
  53.         if(curr.vertex == v2) vertex[v1]->remove(curr);
  54.         else numEdge++;
  55.         vertex[v1]->insert(it);
  56.     }
  57.     void delEdge(int v1, int v2){
  58.         Edge curr;
  59.         vertex[v1]->getValue(curr);
  60.         if(curr.vertex != v2)
  61.             //循环直到找到顶点v2
  62.             for(vertex[v1]->setStart();vertex[v1]->getValue(curr);vertex[v1]->next())
  63.                 if(curr.vertex >= v2) break;
  64.         if(curr.vertex == v2){
  65.             vertex[v1]->remove(curr);
  66.             numEdge--;
  67.         }
  68.     }
  69.     int weight(int v1, int v2){
  70.         Edge curr;
  71.         vertex[v1]->getValue(curr);
  72.         if(curr.vertex != v2)
  73.             //循环直到找到顶点v2
  74.             for(vertex[v1]->setStart();vertex[v1]->getValue(curr);vertex[v1]->next())
  75.                 if(curr.vertex >= v2) break;
  76.         if(curr.vertex == v2) return curr.weight;
  77.         else return 0;
  78.     }
  79.     int getMark(int v){ return mark[v]; }
  80.     void setMark(int v, int val){ mark[v] = val; }
  81. }

4、图的周游（遍历）

一次遍历可能无法全部遍历到，一个数组保存所有节点访问状态，遍历过的就标记。
每个节点vertex执行一次遍历算法：
vertex已被访问，则无需执行，
vertex已被访问，则执行遍历。

  1. void graphTraverse(const Graph* G){
  2.     for(v = 0;v < G->n(); v++)
  3.         G->setMark(v, UNVISITED);
  4.     for(v = 0;v < G->n();v++)
  5.         if(G->getMark(v) != UNVISITED)
  6.             doTraverse(G, v);    //从图G的v顶点开始遍历。
  7. }
  9. //深度优先遍历
  10. //递归调用先天特性 就符合 深度优先的特点
  11. void DFS(Graph* G, int v){
  12.     // PreVisit(G, v); // 访问节点前做点啥
  13.     G->setMark(v, UNVISITED);
  14.     for(int w = G->first(v); w < G->n(); w = G->next(v, w))
  15.         if(G->getMark(w) == UNVISITED) DFS(G, w);
  16.     // PostVisit(G, v);    // 访问节点后做点啥
  17. }
  19. //广度优先遍历：先访问直接相连的点。
  20. //需要用一个队列来实现。
  21. void BFS(Graph* G, int start, Queue<int>* Q){
  22.     int v, w;
  23.     q->enqueue(start);
  24.     G->setMakr(start, VISITED);
  25.     while(Q->lengt()!=0)
  26.         Q->dequeue(v);
  27.         // PreVisit(G, v);    //访问节点前做点啥
  28.         for(int w = G->first(v); w < G->n(); w = G->next(v, w))
  29.             if(G->getMark(w) == UNVISITED) BFS(G, w);
  30.         // PostVisit(G, v);    //访问节点后做点啥
  31. }

5、拓扑排序

优先访问顶点的“所有前顶点”规则的遍历。
有向图DAG才有拓扑排序。
比如工作任务必须先执行全部的先决任务（即“入边”或者是前顶点）。
image.png

  1. //拓扑排序算法（PostVisit版深度优先）
  2. //注意最终输出的是“逆”拓扑排序！！还要再把结果序列颠倒一下。
  3. //所以以下不是完整的拓扑排序！！！！
  4. void topsort(Graph* G){
  5.     int i;
  6.     for(i = 0;i < G->n(); i++) G->setMark(i, UNVISITED);
  7.     for(i = 0;i < G->n(); i++)    //可能存在孤立的顶点，所以每个都要进行一次拓扑。
  8.         if(G->getMark(i) == UNVISITED)
  9.             tophelp(G, i);
  10. }
  11. void tophelp(Graph* G, int v){
  12.     G->setMark(v, VISITED);
  13.     //printout(v);    //注意！不是在previsit打印，
  14.                     //如果是在这里打印，倒序之后就不符合拓扑排序。
  15.     for(int w = G->first(v); w < G->n(); w = G->next(v, w))
  16.         if(G->getMark(w) == UNVISITED)
  17.             tophelp(G, w);
  18.     printout(v);    //必须在postvisit打印。
  19. }
  21. //基于队列的拓扑排序算法
  22. //算法原理：
  23. //    1、保存每个顶点的“前”顶点数包括：
  24. //             直接“前”顶点
  25. //            “间接前”顶点，如a->b->c>d，ab是d的间接前顶点。
  26. //            其实就是所有先决条件（任务）
  28. //    2、没“前”顶点的顶点才能入队。
  30. //    3、出队时，后续所有相连顶点的顶点数-1：
  31. //            相当于执行当前任务，
  32. //            也算是为其他相关顶点减了个先决“任务”
  33. void topsort(Graph* G, Queue<int>* Q){
  34.     int Count[G->n()];
  35.     int v, w;
  36.     for(v = 0; v < G->n(); v++) Count[v] = 0;
  37.     for(v = 0; v < G->n(); v++)
  38.         for(w = G->first(v); w < G->n(); w = G->next(v, w))
  39.             Count[w]++;        //上面注释第1步：记录“前”顶点数
  40.     for(v = 0; v < G->n(); v++)
  41.         if(Count[v] == 0)
  42.             Q->enqueue(v);    //上面注释第2步：
  43.     while(Q->length() != 0){
  44.         Q->dequeue(v);        //上面注释第3步：
  45.         printout(v);
  46.         for(w = G->first(v); w < G->n(); w = G->next(v, w)){
  47.             Count[w]--;        //上面注释第3步
  48.             if(Count[w] == 0) Q->enqueue(w);    //上面注释第2步
  49.         }
  50.     }
  51. }

6、（单源）最短路径原则

给定一个顶点，找出到所有其他顶点的最短路径。
如下图，求A到D的最短路径。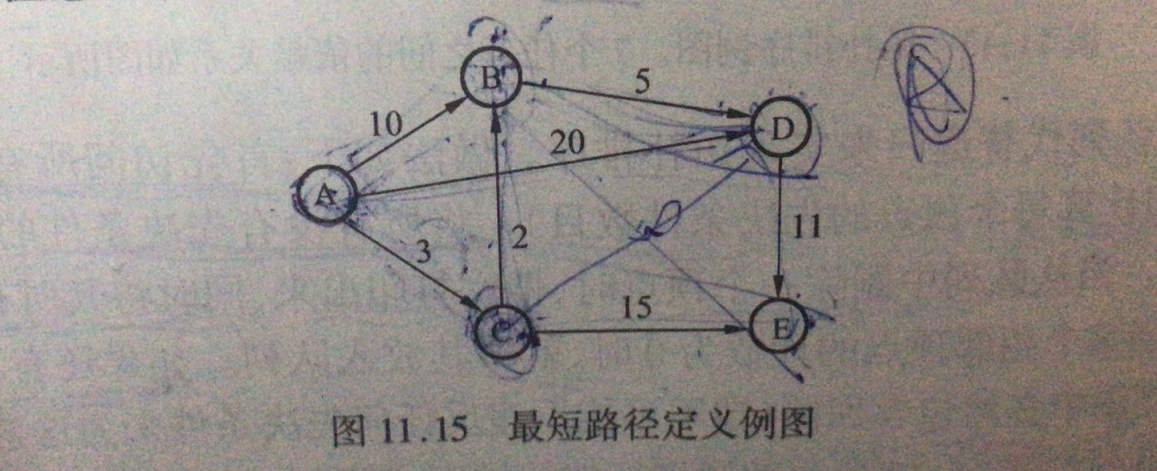
image.png

Dijkstra算法

算法思想：
下面是伪数学表达式，不是严格成立，但符合大脑思考方式。
d(s, vn+j) = d(s, v) + d(v, v)
v图中非s顶点。
d**(s, v)：顶点 v 距离 顶点 s 的“目前”最短距离。
d(v, v)：顶点v到直接相连的顶点v的距离（边权）。
从实际实现上，d只能算是目前掌握到的“目前最短距离”，我们必须顶点遍历完才是“真正最短距离”**。所以遍历的过程，最短距离不断接近准确值。
这里也反应了一个问题，就是求顶点v到顶点s的最短路径，其实是求所有顶点到s的最短路径。

算法复杂度：O( **|V|2 )**

  1. //寻找顶点s到所有其他顶点的最短距离
  2. //D：保存每个顶点到s顶点的“目前”最短距离
  3. //s：目标顶点s
  4. //初始状态，D[s] = 0，其他都 = INFINITY。
  5. void Dijkstra(Graph* G, int* D, int s){
  6.     int i;
  7.     int v;        //在D中，s的最近顶点
  8.     int w;        //w是v能next到的顶点
  9.     for(i = 0; i < G->n(); i++){
  10.         v = minVertex(G, D);    //找出离s“最近”顶点v。
  12.         //顶点v与s是“目前”不相连的，
  13.         //就是目前还没有距离信息，还没遍历到。
  14.         if(D[v] == INFINITY) return;    
  16.         G->setMark(v, VISITED);        //避免重复访问
  18.         //算法核心：根据目前的D（目前最短距离）
  19.         for(w = G->first(v); w < G->n(); w = G->next(v, w))
  21.             //s到v的目前最短距离 + v与顶点w相连的权边 < s到w的目前最短距离。
  22.             if(D[w] > (D[v] + G->weight(v, w)))    
  24.                 //更新s到w的最短距离为：s到v最短距离 + v到w的权边
  25.                 D[w] = D[v] + G->weight(v, w);
  26.     }
  27. }
  29. //找出D中的最小值，而且是未访问的节点。
  30. int minVertex(Graph* G, int* D){
  31.     int i, v;
  32.     for(i = 0; i < G->n(); i++)
  33.         if(G->getMark(i) == UNVISITED){
  34.             v = i;
  35.             break;
  36.         }
  37.     for(i++; i < G->n();i++)
  38.         if((G->getMark(i) == UNVISITED) && (D[i] < D[v]))
  39.             v = i;
  40.     return v;
  41. }

Dijkstra算法（优先队列）

核心思想相同，但是用了最小值堆来找最短距离顶点。
算法复杂度：O( (|V| + |E|) * log |E| )
密集图时，复杂度接近：O( |V|**2* log |E| )

  1. //保存每个顶点的索引和
  2. class DijkElem{
  3. public:
  4.     int vertex, distance;
  5.     DijkElem(){ vertex = -1; distance = -1; }
  6.     DijkElem(int v, int d){ vertex = v; distance = d; }
  7. }
  9. //返回
  10. void Dijkstra( Graph* G, int* D, int s ){
  11.     int i, v, w;
  12.     DijkElem temp(s, 0);
  13.     DijkElem E[G->e()];
  14.     E[0] = temp;
  15.     minheap<DijkElem, DDComp> H(E, 1, G->e());    //堆目前有1个元素，堆总空间G->e()
  16.                                                 //保存未被访问的顶点，各节点就是目前到s
  17.                                                 //最短距离的顶点
  18.     for(i = 0; i < G->n(); i++){
  19.         do{
  20.             if(!H.removemin(temp))     //取出根节点，也就是最短值节点
  21.                 return;    //堆没有节点了
  22.             v = temp.vertex;
  23.         }while(G->getMark(v) == VISITED);
  24.         G->setMark(v, VISITED);
  25.         if(D[v] == INFINITY) return;
  26.         for(w = G->first(); w < G->n(); w = G->next(v, w))
  27.             if(D[w] > (D[v] + G->weight(v, w))){
  28.                 D[w] = D[v] + G->weight(v, w);
  29.                 temp.distance = D[w];
  30.                 temp.vertex = w;
  31.                 H.insert(temp);
  32.             }
  33.     }
  34. }

算法分析

核心思想相同，但查找目前最短距离顶点的上各做了“取舍”。
minvertex是扫描数组，找的更慢点但找的稳定，不怕多，
minheap是最小值堆，是找的更快点但找的不稳定，多了代价就大。

minvertex：算法复杂度：O( **|V|2 )
minheap： 算法复杂度：O( (|V| + |E|) log |E| )*

边数过多时（密集图）：

minvertex：算法复杂度：O( **|V|2 )
minheap： 算法复杂度：O( |V|2 * log |E| )

因为每多一条边，堆的元素就+1，都要重排一次。

7、双源最短路径

找每对顶点的最短长度路径。
复杂度：O（**|V|**）**
密集图最好选择，较容易实现。

  1. void Floyd(Graph* G){
  2.     int D[G->n()][G->n()];
  3.     for(int i = 0; i < G->n(); i++)
  4.         for(int j = 0; j < G->n(); j++)
  5.             D[i][j] = G->weight(i, j)    //初始化为任意两点之间的权重。
  6.     for(int k = 0; k < G->n(); k++)
  7.         for(int i = 0; i < G->n(); i++)
  8.             for(int j = 0; j < G->n(); j++)
  9.                 if(D[i][j] > (D[i][k] + D[k][j]))
  10.                     D[i][j] = D[i][k] + D[k][j];
  11. }

8、最小支撑树MST

minimum-cost spanning tree。
数学定义：G是连通无向图，MST是下图中的一个：包含所有顶点和部分边的连通图。所有边之和是所有这些图中最小的。
加深理解：把所有城市连在一起的，路长度最小的路线。
没有回路，所以是|V| - 1条边的树结构。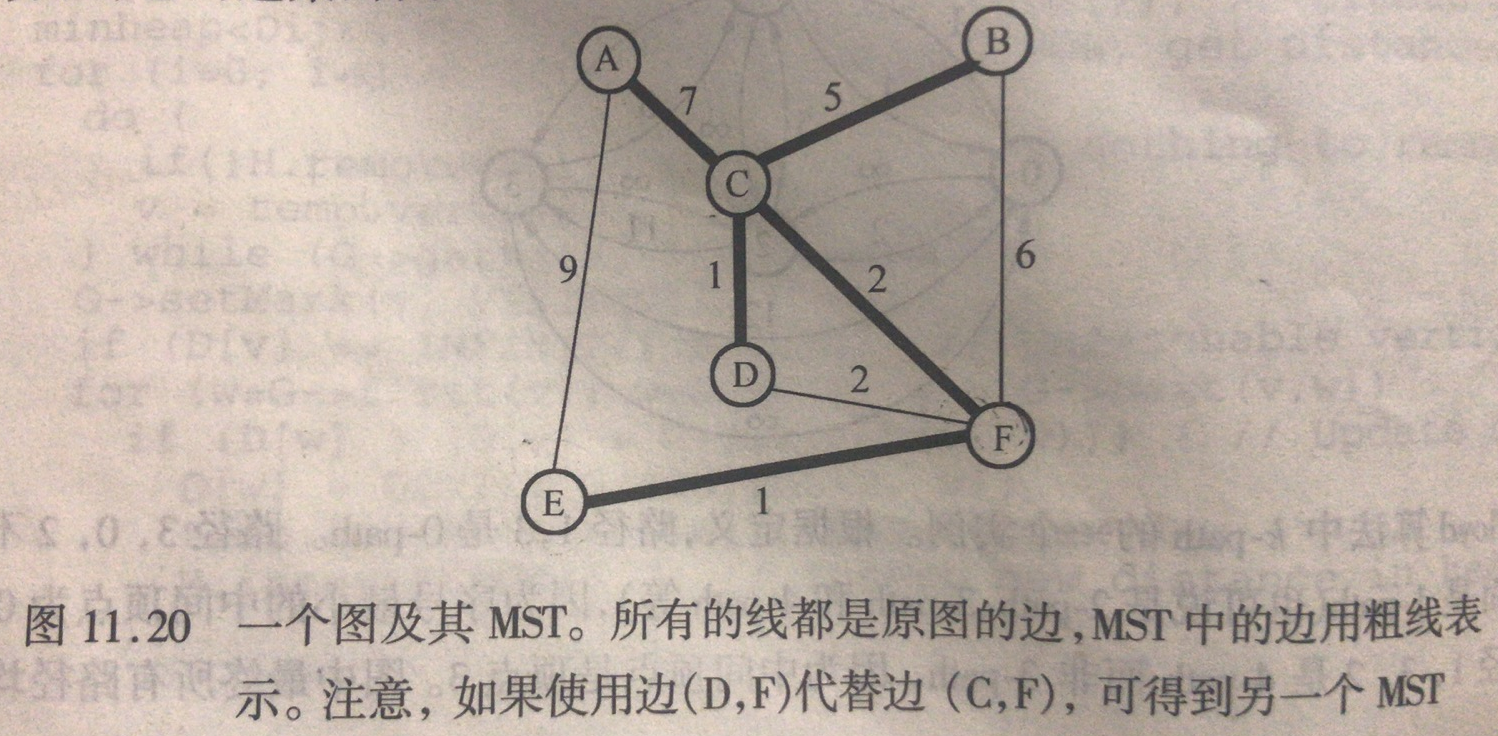
image.png

求最小支撑树：Prim算法

0、初始顶点N
1、找出N的最小权边的顶点N
2、找出与N、N相连的最小权边的点N
3、……
4、找出与N、……、N相连的最小权边N

  1. //D：保存与各个索引顶点的相连的最小权边
  2. //     其实D[s] = 0，其他 = INFINITY
  3. //s：起始顶点
  4. //类似最短路径算法。
  5. void Prim(Graph* G, int* D, int s){
  6.     int V[G->n()];    //V存储MST树节点，V[v]=w，顶点v和w直接相连。
  7.     int i, w;
  8.     for(i = 0; i < G->n(); i++){
  9.         int v = minVertex(G, D);
  10.         G->setMark(v, VISITED);
  11.         if(v != s) AddEdgetToMST(V[v], v);
  12.         if(D[v] == INFINITY) return;
  13.         for(w = G->first(v); w < G->n(); w = G->next(v, w))
  14.             if(D[w] > G->weight(v, w)){ //w当前保存的最小权边 比vw边更大，替换掉
  15.                 D[w] = G->weight(v, w);    //v，next到w的权最小
  16.                 V[w] = v;    //w顶点来来源是v。
  17.             }
  18.     }
  19. }
  21. //使用优先队列的Prim
  22. //类似最短路径算法的优先队列。
  23. void Prim(Graph* G, int* D, int s){
  24.     int i, v, w;
  25.     int V[G->n()];
  26.     DijkElem temp;
  27.     DijkElem E[G->e()];
  28.     temp.distance = 0;
  29.     temp.vertex = s;
  30.     E[0] = temp;
  31.     minheap<DijkElem, DDComp> H(E, 1, G->e());
  32.     for(i = 0; i < G->n(); i++){
  33.         do{
  34.             if(!H.removemin(temp)) return;
  35.             v = temp.vertex;
  36.         }while(G->getMark(v) == VISITED);
  37.         G->setMark(v, VISITED);
  38.         if(v != s) AddEdgetToMST(V[v], v);
  39.         if(D[v] == INFINITY) return;
  40.         for(w = G->first(v); w < G->n(); w = G->next(v, w))
  41.             if(D[w] > G->weight(v, w)){
  42.                 D[w] = G->weight(v, w);
  43.                 V[w] = v;
  44.                 temp.distance = D[w];
  45.                 temp.vertex = w;
  46.                 H.insert(temp);
  47.             }
  48.     }
  49. }

求最小支撑树：Kruskal算法

算法复杂度：
最差O（**|E| log |E|**）
一般O（**|V| log |E|**）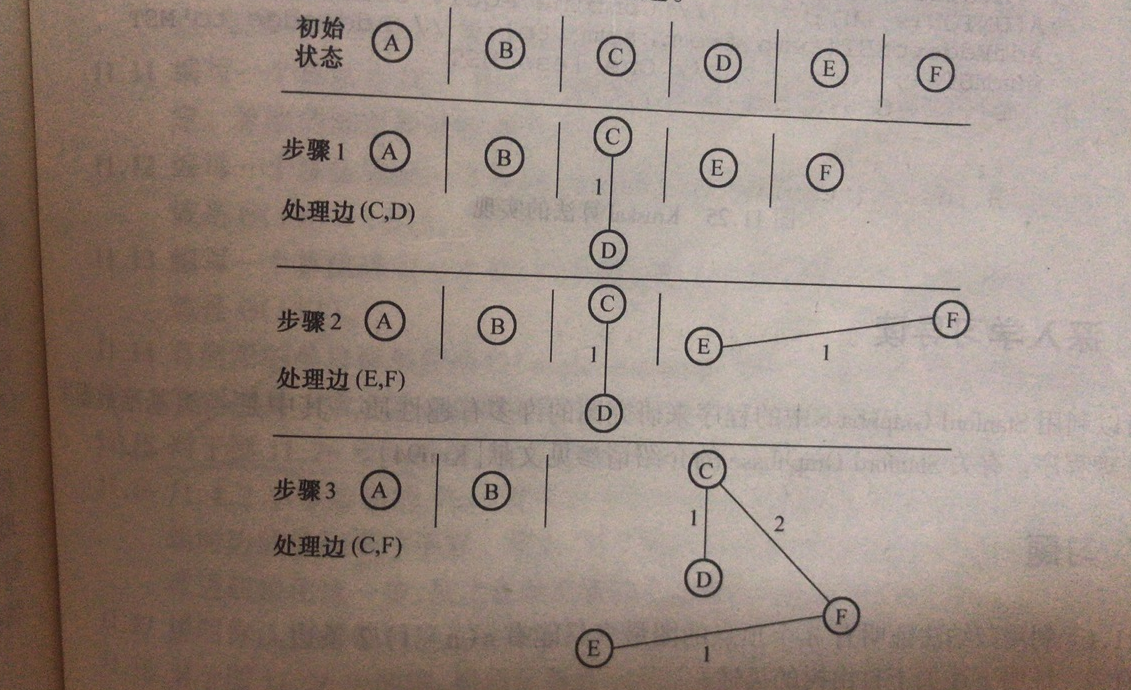
image.png
1、将所有顶点分为|V|个等价类。（UNION/FIND树）
2、优先处理权最小的边，边把两个等价类相连，则合并等价类
3、重复2步骤。
4、最后只剩一个等价类。