🥉Easy

给定一个二叉树和一个目标和，判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和。

说明: 叶子节点是指没有子节点的节点。

示例:
给定如下二叉树，以及目标和 sum = 22，

  1.               5
  2.              / \
  3.             4   8
  4.            /   / \
  5.           11  13  4
  6.          /  \      \
  7.         7    2      1

返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2。

题解

核心思路肯定是对树进行遍历。

广度优先遍历

使用广度优先搜索，记录根节点到当前节点的路径和，BFS 使用 队列 保存遍历到每个节点时的路径和，如果该节点恰好是叶子节点，并且 路径和 正好等于 sum，说明找到了解。以防重复计算。这样可以使用两个队列，分别存储将要遍历的节点，以及根节点到这些节点的路径和即可。如下图所示：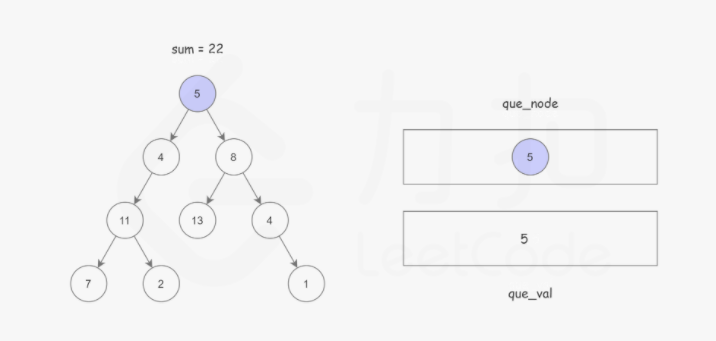
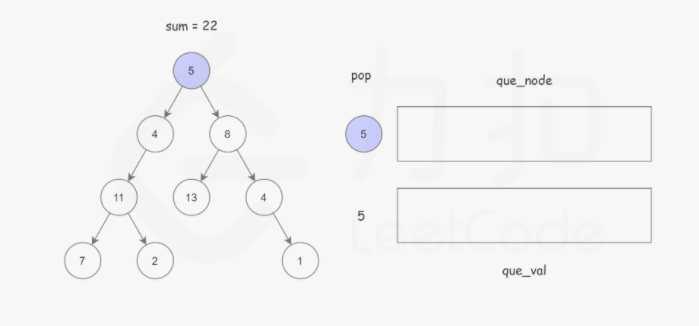
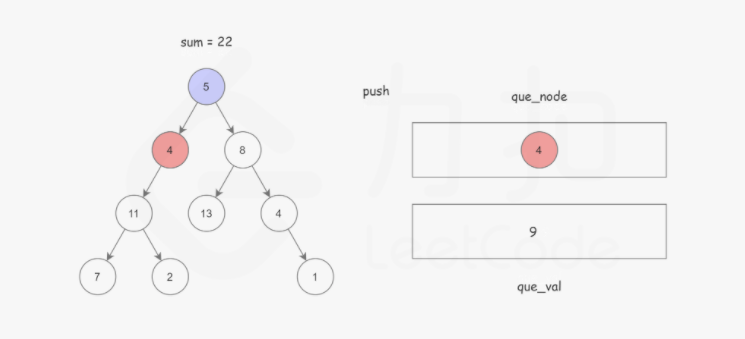
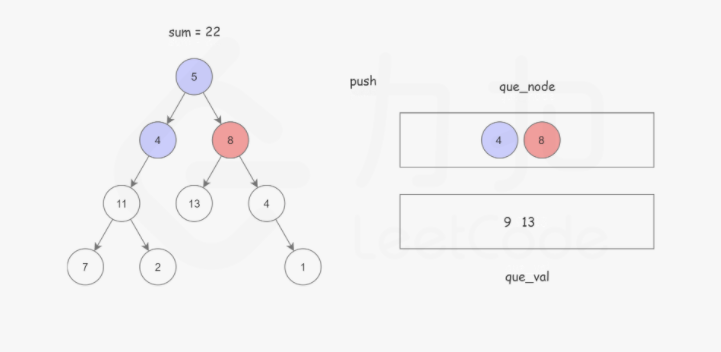
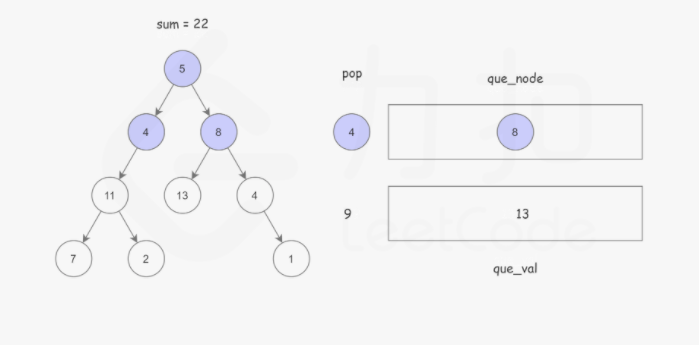
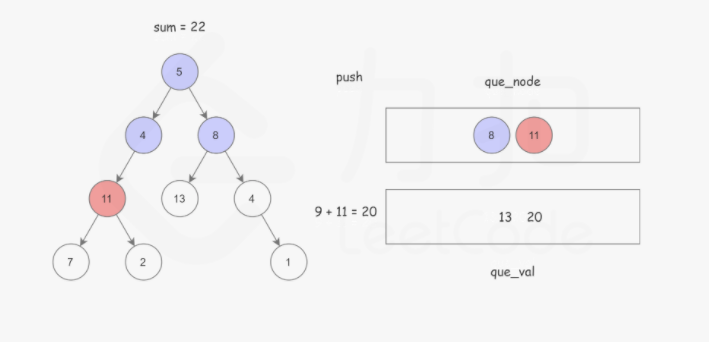
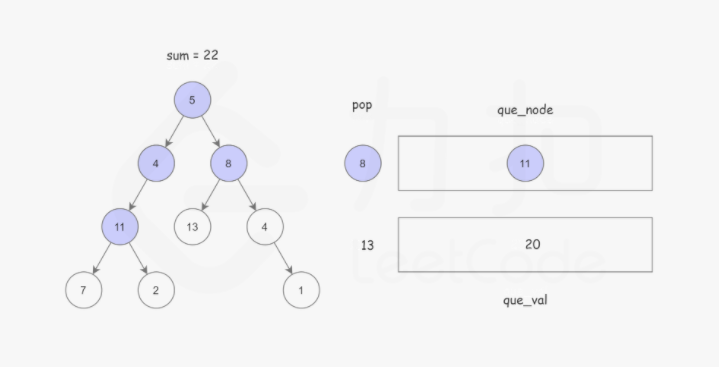
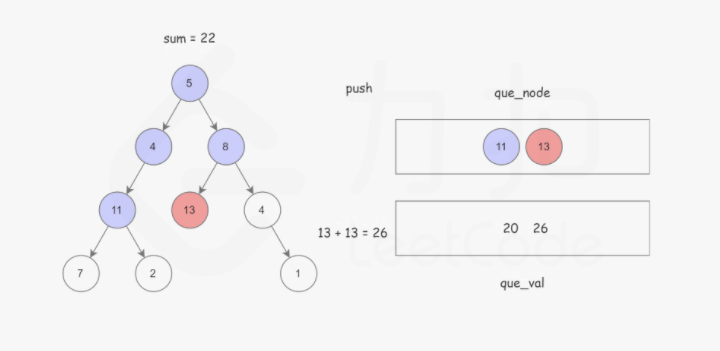
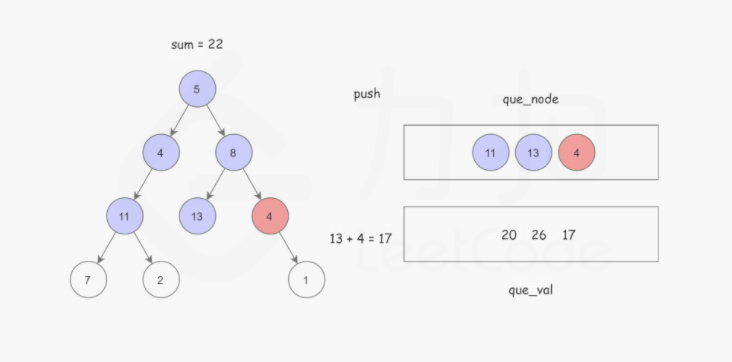
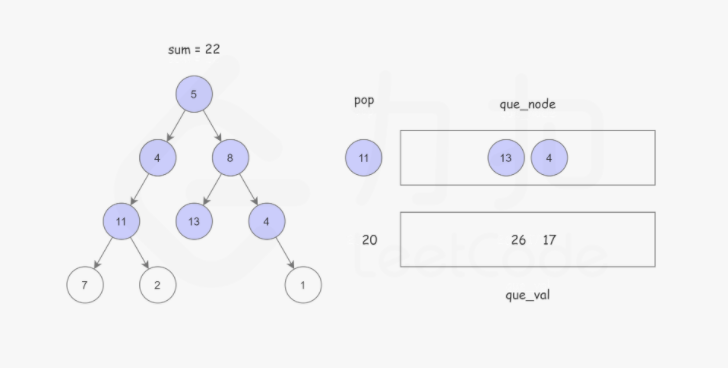
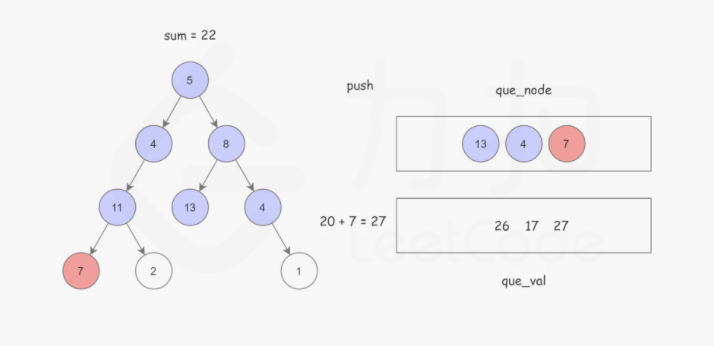
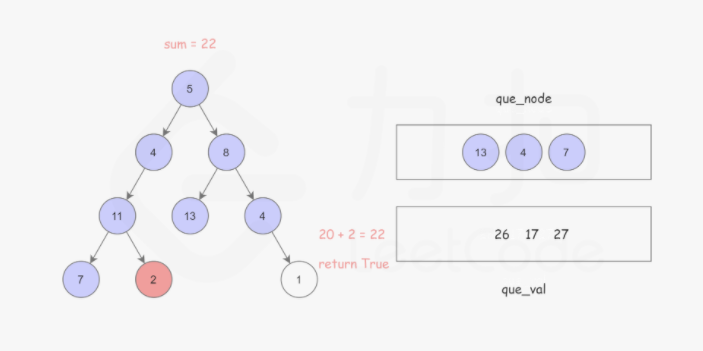
image.png
image.png
image.png
image.png
image.png
image.png
image.png
image.png
image.png
image.png
image.png
image.png

Python

  1. class Solution:
  2.     def hasPathSum(self, root: TreeNode, sum: int) -> bool:
  3.         if not root:
  4.             return False
  5.         que_node = collections.deque([root])
  6.         que_val = collections.deque([root.val])
  7.         while que_node:
  8.             now = que_node.popleft()
  9.             temp = que_val.popleft()
  10.             if not now.left and not now.right:
  11.                 if temp == sum:
  12.                     return True
  13.                 continue
  14.             if now.left:
  15.                 que_node.append(now.left)
  16.                 que_val.append(now.left.val + temp)
  17.             if now.right:
  18.                 que_node.append(now.right)
  19.                 que_val.append(now.right.val + temp)
  20.         return False

深度优先遍历

Python

  1. # Definition for a binary tree node.
  2. # class TreeNode(object):
  3. #     def __init__(self, x):
  4. #         self.val = x
  5. #         self.left = None
  6. #         self.right = None
  8. class Solution(object):
  9.     def hasPathSum(self, root, sum):
  10.         """
  11.         :type root: TreeNode
  12.         :type sum: int
  13.         :rtype: bool
  14.         """
  15.         if not root: return False
  16.         if not root.left and not root.right:
  17.             return sum == root.val
  18.         return self.hasPathSum(root.left, sum - root.val) or self.hasPathSum(root.right, sum - root.val)

一直向下找到叶子节点，如果到叶子节点时sum == 0，说明找到了一条符合要求的路径。

JavaScript

  1. const hasPathSum = (root, sum) => {
  2.   if (root == null) return false;                // 遍历到null节点
  3.   if (root.left == null && root.right == null) { // 遍历到叶子节点
  4.     return sum - root.val == 0;                  // 如果满足这个就返回true
  5.   }
  6.   return hasPathSum(root.left, sum - root.val) ||
  7.     hasPathSum(root.right, sum - root.val);      // 大问题转成两个子树的问题
  8. }