实现一个基本的计算器来计算一个简单的字符串表达式 s 的值。

示例 1：

  1. 输入：s = "1 + 1"
  2. 输出：2

示例 2：

  1. 输入：s = " 2-1 + 2 "
  2. 输出：3

示例 3：

  1. 输入：s = "(1+(4+5+2)-3)+(6+8)"
  2. 输出：23

提示：

  • 🥇 224. 基本计算器 - 图1
  • s 由数字、’+’、’-‘、’(‘、’)’、和 ‘ ‘ 组成
  • s 表示一个有效的表达式

题解

感觉不难，实际上无从下笔，明后天面试咋办！！！😿

栈

参考
一个表达式分为三部分：

左边表达式①，运算符③， 右边表达式②

本题中，左边和右边的表达式可以是一个数字，也可以是一个括号包起来的表达式；运算符可以是加减。
一个只包含加减和括号的表达式，可以从左到右计算，遇到括号就先算括号里面的。具体来说就是先计算左边的表达式，再计算右边表达式，最后根据运算符，计算 ①和②的运算 。

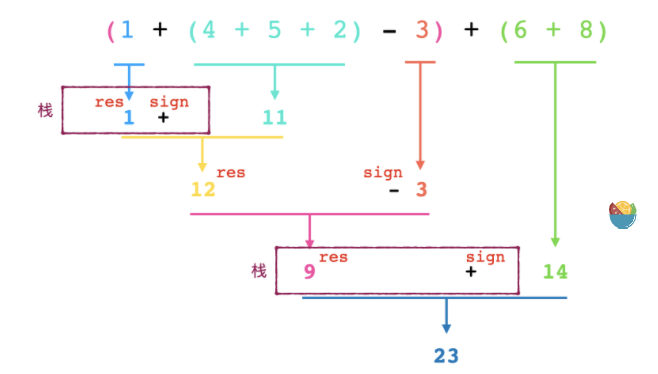
用题目示例 “(1+(4+5+2)-3)+(6+8)“ 来说明运算符计算的顺序：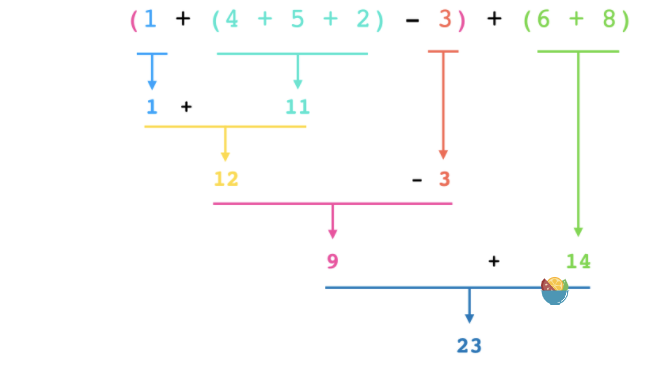
image.png
要计算表达式的时候，需要先计算👈左边表达式①，然后把①的结果和运算符③保存起来，再计算👉右边表达式②，最后计算①和②，这就是一个递归的过程。

递归的过程可以用栈来模拟：栈保存左边表达式①的计算结果和运算符③，在计算右边表达式②的结果之后，从栈中取出运算符③和①的结果，再进行计算整个表达式的结果。

例如：(1 + (2 + (3 + 4)))。栈顶保留的是最里层嵌套的运算，弹出栈的时候，正好先算的是最里面括号的，再算外边括号的。这种情况时，栈里面保存的是 [“1”, “+”, “2”, “+”, “3”, “+”]，然后遇到 4，此时计算的是 3 + 4，然后算 7 + 2，再算 9 + 1。可以通过递归来帮助理解。

代码里面:

  • res 表示左边表达式除去栈内保存元素的计算结果；
  • sign 表示运算符；
  • num 表示当前遇到的数字，会更新到 res 中；
  • 用栈保存遇到左括号时前面计算好了的结果和运算符。

操作的步骤是：

  • 如果当前是数字，那么更新计算当前数字；
  • 如果当前是操作符+或者-，那么需要更新计算当前计算的结果 res，并把当前数字 num 设为 0，sign 设为正负，重新开始；
  • 如果当前是 ( ，那么说明遇到了右边的表达式，而后面的小括号里的内容需要优先计算，所以要把 res，sign 进栈，更新 res 和 sign 为新的开始；
  • 如果当前是 ) ，那么说明右边的表达式结束，即当前括号里的内容已经计算完毕，所以要把之前的结果出栈，然后计算整个式子的结果；
  • 最后，当所有数字结束的时候，需要把最后的一个 num 也更新到 res 中。

image.png
还要注意字符串中可能有空格！

Python

  1. def calculate(s):
  2.     res,num,sign = 0,0,1
  3.     stack=[]
  4.     for c in s:
  5.         if c.isdigit():
  6.             num = 10*num+int(c) # 这里10*num是为了避免出现连续两个数的情况，比如12，num就应该是1*10+2
  7.         elif c == '+' or c == '-':
  8.             res += sign*num
  9.             num=0
  10.             sign=1 if c == '+' else -1
  11.         elif c == '(':
  12.             stack.append(res)
  13.             stack.append(sign)
  14.             res=0
  15.             sign=1
  16.         elif c==')':
  17.             res+=sign*num
  18.             num=0
  19.             res*=stack.pop()
  20.             res+=stack.pop()
  21.     res+=sign*num
  22.     return res

JavaScript

  1. /**
  2.  * @param {string} s
  3.  * @return {number}
  4.  */
  5. var calculate = function(s) {
  6.     let res = 0
  7.     let num = 0
  8.     let sign = 1
  9.     let stack = []
  10.     for(const c of s){
  11.         if (c === ' '){
  12.             continue
  13.         }
  14.         const n = Number(c)
  15.         if (!isNaN(n)){
  16.             num = 10* num + parseInt(n)
  17.         } else if (c === '+' || c === '-') {
  18.             res += sign*num
  19.             num = 0
  20.             if (c === '+') {
  21.                 sign = 1
  22.             } else {
  23.                 sign = -1
  24.             }
  25.         } else if (c === '(') {
  26.             stack.push(res)
  27.             stack.push(sign)
  28.             res = 0
  29.             sign = 1
  30.         } else if (c === ')') {
  31.             res += sign*num
  32.             num = 0
  33.             res *= stack.pop()
  34.             res += stack.pop()
  35.         }
  36.     }
  37.     res += sign*num
  38.     return res
  40. };

复杂度分析

  • 时间复杂度：O(n)，其中 n 为字符串 s 的长度。需要遍历字符串 s 一次，计算表达式的值。
  • 空间复杂度：O(n)，其中 n 为字符串 s 的长度。空间复杂度主要取决于栈的空间，栈中的元素数量不超过 n。