🥈Medium

给定一个机票的字符串二维数组 [from, to]，子数组中的两个成员分别表示飞机出发和降落的机场地点，对该行程进行重新规划排序。所有这些机票都属于一个从 JFK（肯尼迪国际机场）出发的先生，所以该行程必须从 JFK 开始。

说明:
如果存在多种有效的行程，你可以按字符自然排序返回最小的行程组合。例如，行程 [“JFK”, “LGA”] 与 [“JFK”, “LGB”] 相比就更小，排序更靠前
所有的机场都用三个大写字母表示（机场代码）。
假定所有机票至少存在一种合理的行程。
示例 1:
/

  1. 输入: [["MUC", "LHR"], ["JFK", "MUC"], ["SFO", "SJC"], ["LHR", "SFO"]]
  2. 输出: ["JFK", "MUC", "LHR", "SFO", "SJC"]

示例 2:
/

输入: [["JFK","SFO"],["JFK","ATL"],["SFO","ATL"],["ATL","JFK"],["ATL","SFO"]]
输出: ["JFK","ATL","JFK","SFO","ATL","SFO"]
解释: 另一种有效的行程是 ["JFK","SFO","ATL","JFK","ATL","SFO"]。但是它自然排序更大更靠后。

题解

吐槽

还是没有做出来😭，今天面试也是一塌糊涂，今晚要好好准备啊！！！
这道题，我的想法是遍历tickets，先找from等于出发点“JFK”，再将遍历到的对应的to加入一个list中。

  • 如果list里面就一个元素，那此元素就是新的出发点，然后结果数组ans中加入上面的from和to。tickets删除[from, to]。
  • 如果list中不止一个元素，就需要比较list中节点的字典序，选择最小的结果作为to，其他和上面一样

但这样复杂度太高，也不好写

def judge(data):
    # 判断data中字典序最小的
    pass
def findItinerary(tickets):
    begin = "JFK"
    ans = []
    while tickets:
        temp = []
        ans.append(begin)
        for data in tickets:
            if data[0] == begin:
                temp.append(data[1])
        if len(temp) == 1:
            ans.append(temp[0])
        else:
            judge(temp)
    return ans




s = [["MUC", "LHR"], ["JFK", "MUC"], ["SFO", "SJC"], ["LHR", "SFO"]]

题解

看了题解原来是一个欧拉图的问题。本题等同于一笔画问题：给定一个n个点m条边的图，要求从指定顶点出发，经过所有的边恰好一次，使得路径的字典序最小。
**
一笔画问题和欧拉图或半欧拉图有紧密关系。下面是相关定义：

  • 通过图中所有边恰好一次且经过所有顶点的通路叫欧拉通路
  • 通过图中所有边恰好一次且经过所有顶点的回路叫欧拉回路
  • 具有欧拉回路的无向图称为欧拉图
  • 具有欧拉通路但不具有欧拉回路的无向图称为半欧拉图

因为题目保证至少存在一种合理路径，那说明本题的图是欧拉图或半欧拉图，只要输出路径即可。

如果没有保证至少存在一种合理的路径，我们需要判别这张图是否是欧拉图或者半欧拉图，具体地：

  • 对于无向图 G，G 是欧拉图当且仅当 G 是连通的且没有奇度顶点。

  • 对于无向图 G，GG 是半欧拉图当且仅当 G 是连通的且 G 中恰有 2 个奇度顶点。

  • 对于有向图 G，G 是欧拉图当且仅当 G 的所有顶点属于同一个强连通分量且每个顶点的入度和出度相同。
  • 对于有向图 G，G 是半欧拉图当且仅当 G 的所有顶点属于同一个强连通分量且
  • 恰有一个顶点的出度与入度差为 1；
  • 恰有一个顶点的入度与出度差为 1；
  • 所有其他顶点的入度和出度相同。

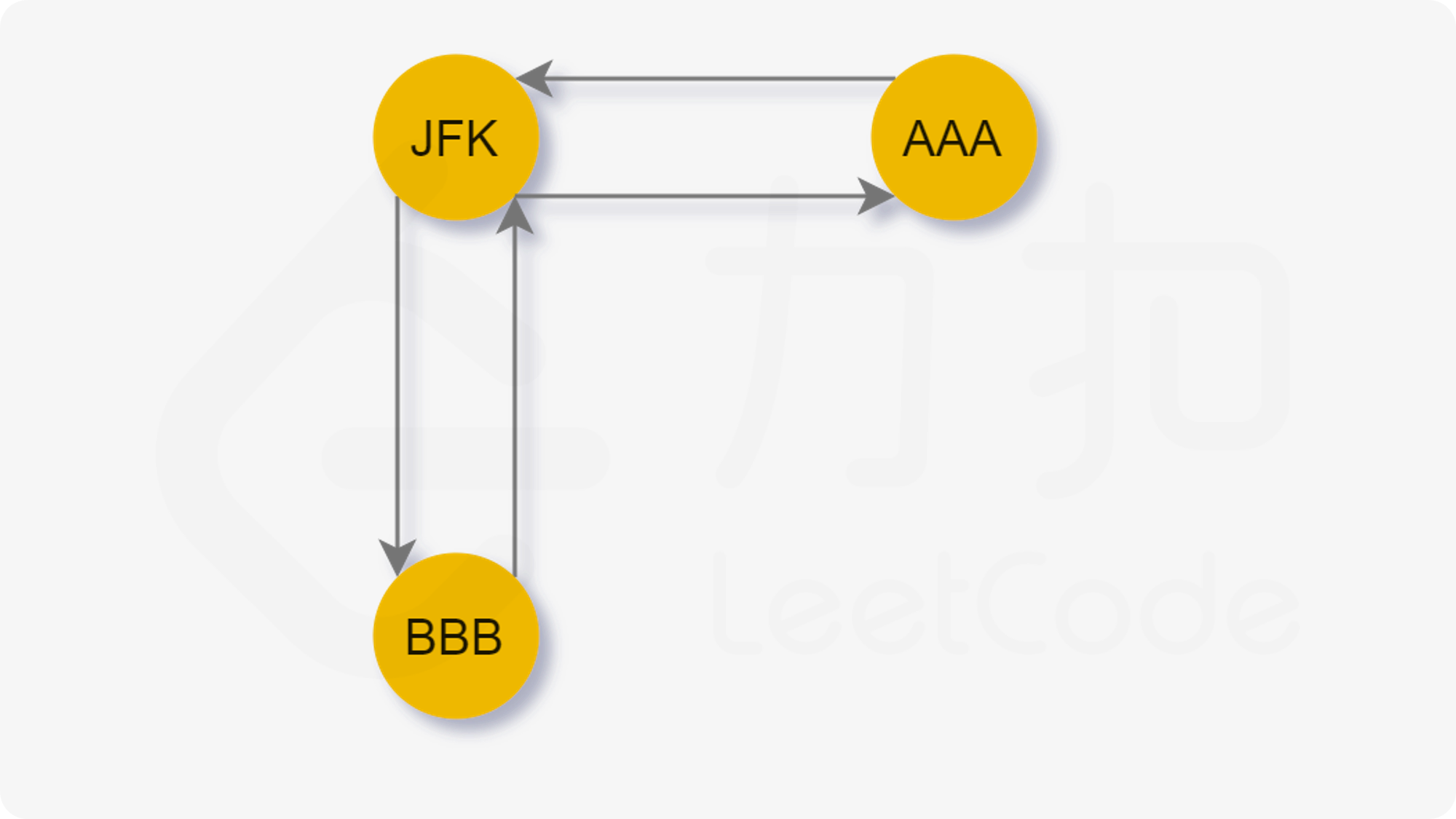
image.png
从起点JFK出发，有两条路径：

  • JFK -> AAA -> JFK -> BBB ->JFK
  • JFK -> BBB -> JFK -> AAA -> JFK

既然要求字典序最小，那么我们每次应该贪心地选择当前节点所连的节点中字典序最小的那一个，并将其入栈。最后栈中就保存了我们遍历的顺序。

为了保证我们能够快速找到当前节点所连的节点中字典序最小的那一个，我们可以使用优先队列存储当前节点所连到的点，每次我们 🥈332. 重新安排行程 - 图2地找到最小字典序的节点，并 🥈332. 重新安排行程 - 图3地删除它。

然后考虑一种特殊情况：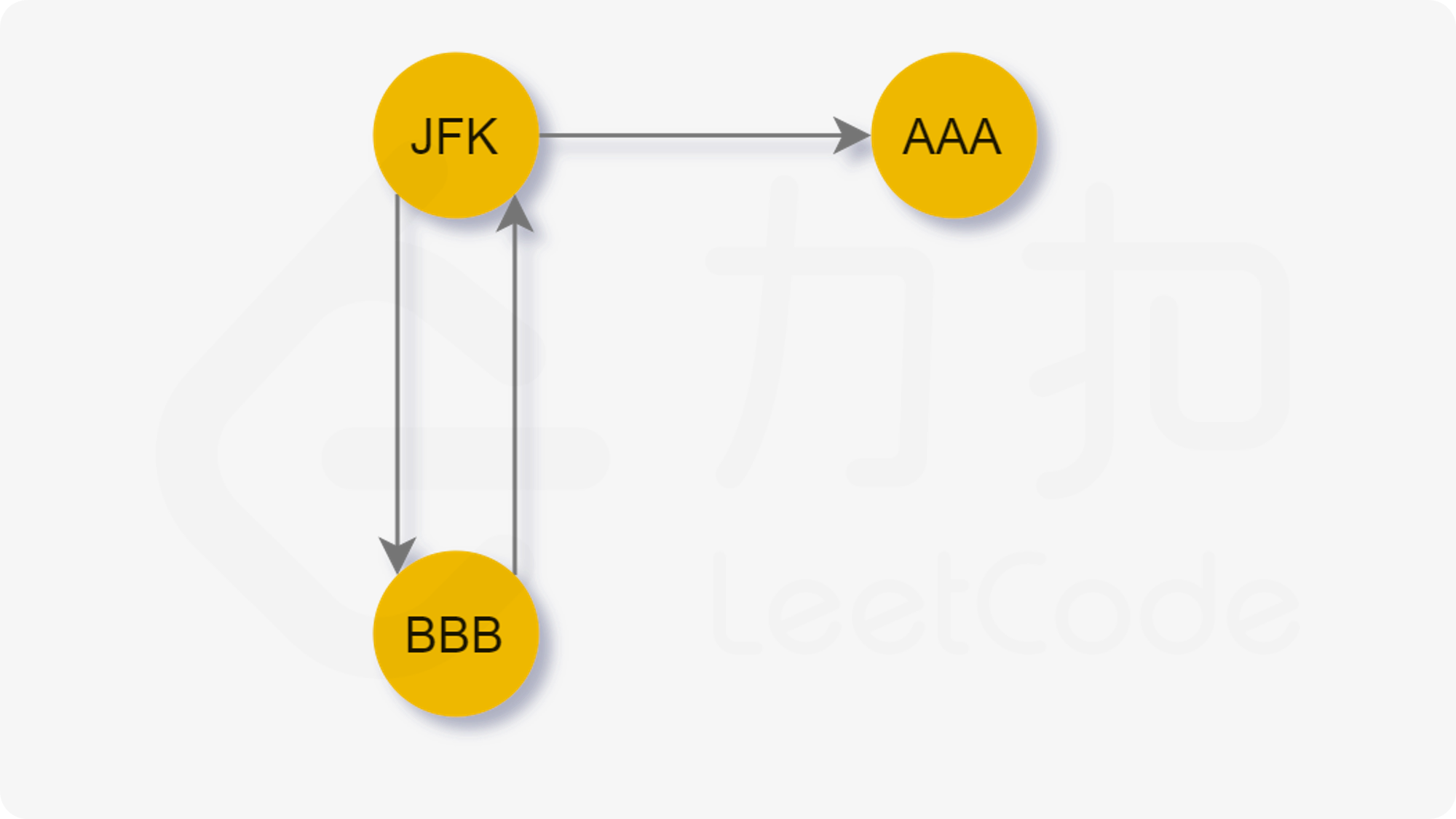
image.png
当先访问 AAA 时，再就无法回到 JFK，这样我们就无法访问剩余的边了。

也就是说，贪心地选择字典序最小的节点前进时，我们可能先走入「死胡同」，从而导致无法遍历到其他还未访问的边。于是我们希望能够遍历完当前节点所连接的其他节点后再进入「死胡同」。

注意对于每一个节点，它只有最多一个「死胡同」分支。依据前言中对于半欧拉图的描述，只有那个入度与出度差为 1 的节点会导致死胡同。

Hierholzer 算法

Hierholzer 算法用于在连通图中寻找欧拉路径，其流程如下：

  1. 从起点出发，进行深度优先搜索。

  2. 每次沿着某条边从某个顶点移动到另外一个顶点的时候，都需要删除这条边。

  3. 如果没有可移动的路径，则将所在节点加入到栈中，并返回。

当我们顺序地考虑该问题时，我们也许很难解决该问题，因为我们无法判断当前节点的哪一个分支是「死胡同」分支。

不妨倒过来思考。我们注意到只有那个入度与出度差为 1 的节点会导致死胡同。而该节点必然是最后一个遍历到的节点。我们可以改变入栈的规则，当我们遍历完一个节点所连的所有节点后，我们才将该节点入栈（即逆序入栈）。

对于当前节点而言，从它的每一个非「死胡同」分支出发进行深度优先搜索，都将会搜回到当前节点。而从它的「死胡同」分支出发进行深度优先搜索将不会搜回到当前节点。也就是说当前节点的死胡同分支将会优先于其他非「死胡同」分支入栈。

这样就能保证我们可以「一笔画」地走完所有边，最终的栈中逆序地保存了「一笔画」的结果。我们只要将栈中的内容反转，即可得到答案。