🕸广度优先搜索(BFS)

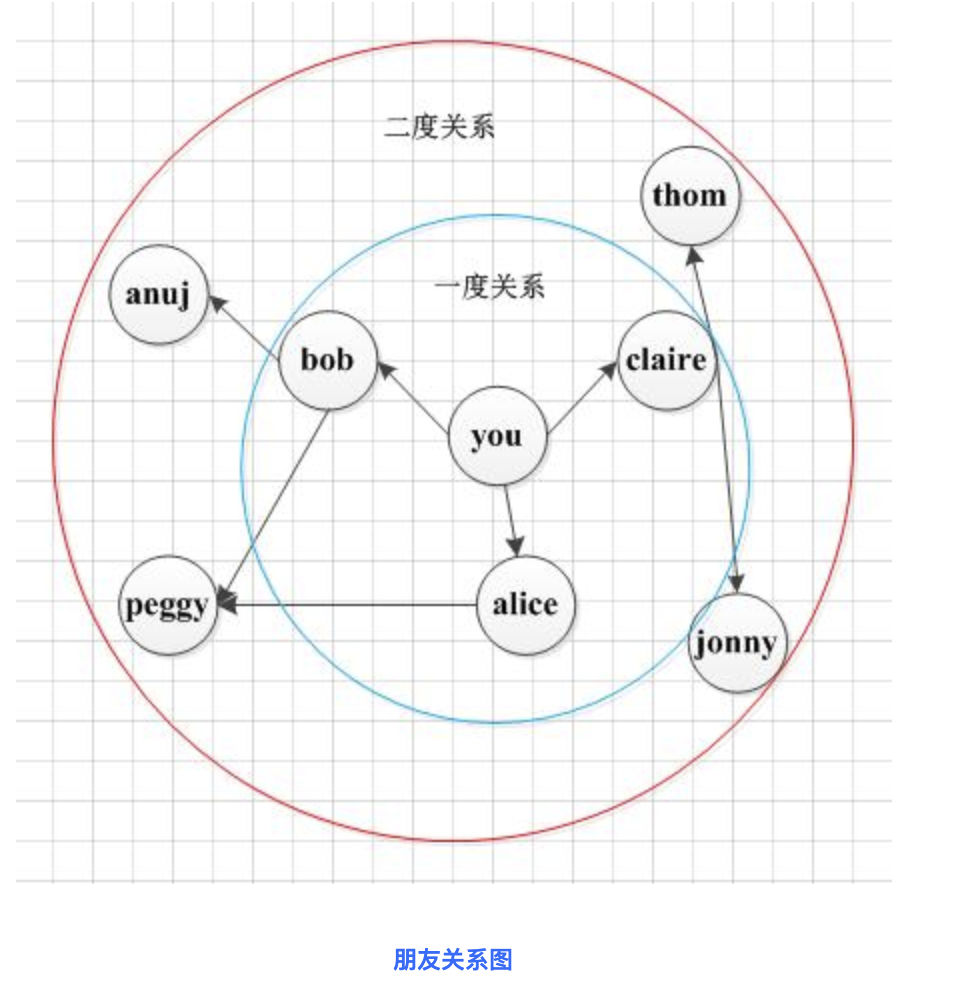
简单的说，BFS是从根节点开始，沿着树的宽度遍历树的节点。如果所有节点均被访问，则算法中止。

BFS是一种暴力搜索算法，目的是系统地展开并检查图中的所有节点，以找寻结果。换句话说，它并不考虑结果的可能地址，彻底地搜索整张图，直到找到结果为止。BFS并不使用经验法则算法。
从算法的观点，所有因为展开节点而得到的子节点都会被加进一个先进先出的队列中。一般的实现里，其邻居节点尚未被检验过的节点会被放置在一个被称为 open 的容器中（例如队列或是链表），而被检验过的节点则被放置在被称为 closed 的容器中。（open-closed表）

下图的朋友关系图就是很形象的广度优先搜索🔍

步骤

1. 首先将根节点放入队列
2. 从队列中取出第一个节点,并检验它是否为目标.
   • 如果找到目标,则结束搜索并回传结果
   • 否则将它所有尚未检验过的直接子节点加入队列中.
3. 若队列为空,表示整张图都检查过了–亦即图中没有欲搜索的目标.结束搜索并回传“找不到目标”。
4. 重复步骤2.
5. 需要使用队列这一数据结构

如图所示：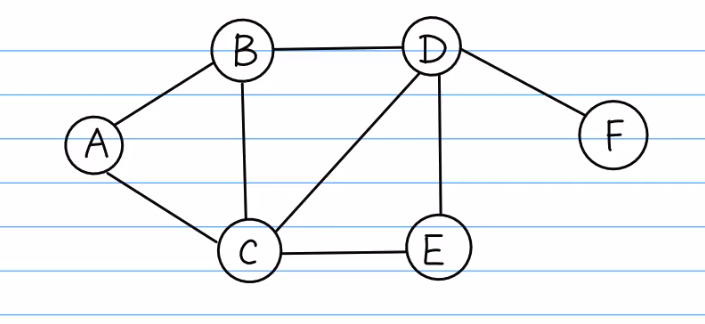

假设以A为起点,与A点直接相连的点是 B,C ,此时广度优先遍历序列为A,B,C, 将BC入队,此时与B节点直接相连的是C和D,C已经在Queue中,所以下一个节点应是D,此时队列中为ABCD.与C节点相连的且未遍历过的节点为E, 所以将E入队,此时未遍历的节点为D,E, 与D直接相连的节点F入队即可得到广度优先遍历ABCDEF.

算法框架

BFS本质上就是一幅「图」，从一个起点，走到终点，问最短路径

BFS 出现的常见场景本质就是在一幅「图」中找到从起点 start 到终点 target 的最近距离
**
记住下面的框架就可以了

// 计算从起点 start 到终点 target 的最近距离
int BFS(Node start, Node target) {
    Queue<Node> q; // 核心数据结构
    Set<Node> visited; // 避免走回头路
    q.offer(start); // 将起点加入队列
    visited.add(start);
    int step = 0; // 记录扩散的步数
    while (q not empty) {
        int sz = q.size();
        /* 将当前队列中的所有节点向四周扩散 */
        for (int i = 0; i < sz; i++) {
            Node cur = q.poll();
            /* 划重点：这里判断是否到达终点 */
            if (cur is target)
                return step;
            /* 将 cur 的相邻节点加入队列 */
            for (Node x : cur.adj())
                if (x not in visited) {
                    q.offer(x);
                    visited.add(x);
                }
        }
        /* 划重点：更新步数在这里 */
        step++;
    }
}

代码

Python

graph = {
    "A":["B", "C"],   # 与A相连的节点是B,C 
    "B":["A", "C", "D"], # 与B相连的节点是A,C,D
    "C":["A", "B", "D", "E"],
    "D":["B", "C", "E", "F"],
    "E":["C", "D"],
    "F":["D"]
 }
def BFS(graph, s):
    queue = []  # 初始化一个空队列
    queue.append(s) # 将所有节点入队列
    seen = set() # 用来判断现在遍历的节点之前有没有被遍历过
    seen.add(s)
    parent = {s : None}
    while(len(queue) > 0):
        # 弹出栈中元素
        vertex = queue.pop(0)
        # 获取与元素相连接的节点
        nodes = graph[vertex]
        # 遍历节点
        for w in nodes:
            # 如果这个节点之前没有被遍历过
            if w not in seen:
                # 就加入栈中
                queue.append(w)
                seen.add(w)
                parent[w] = vertex
    return parent
parent = BFS(graph, "E")
for key in parent:
    print(key, parent[key])

JavaScript

function BFS (graph, node) {
    queue = [node]
    seen = new Set()
    seen.add(node)
    parent = { }
    while (queue.length > 0) {
        let a = queue.shift()
        let nodes = graph[a]
        for( let k in nodes){
            if (!seen.has(nodes[k])){
                queue.push(nodes[k])
                seen.add(nodes[k])
                parent[nodes[k]] = a
            }
        }
    }
    return parent
}

广度优先寻找最短路径

下图是使用 BFS 算法搜寻出来的一条路径：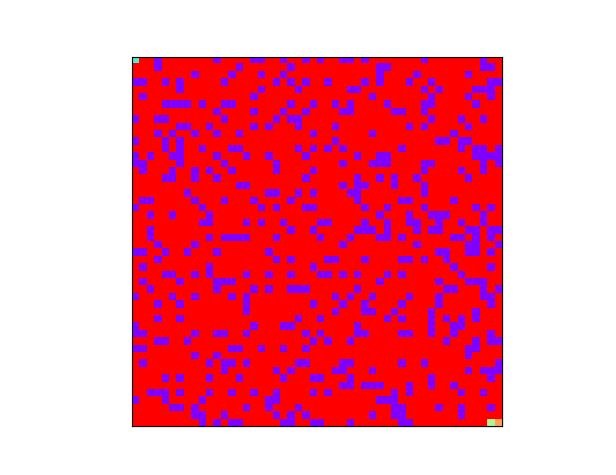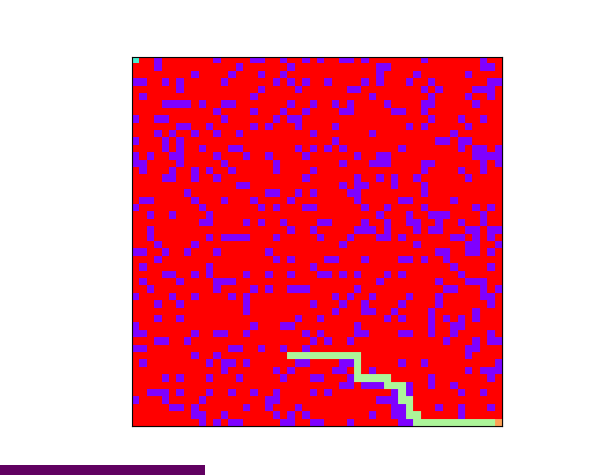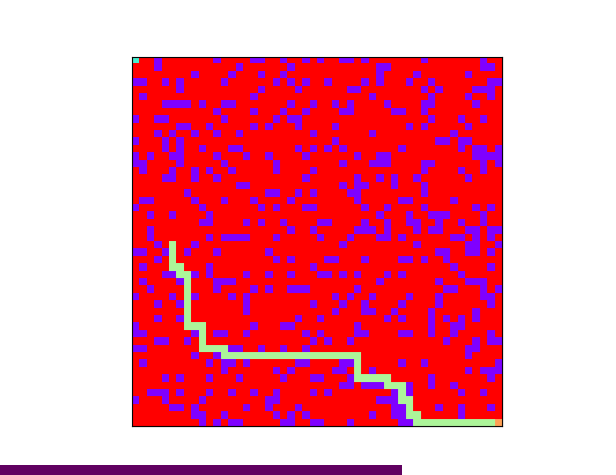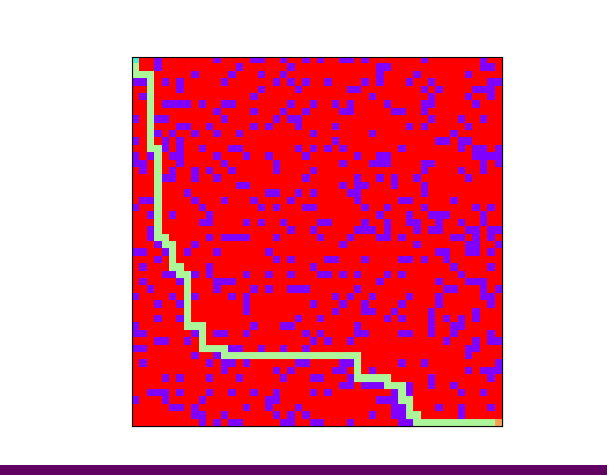

使用广度优先算法搜寻迷宫路径的过程如下：从迷宫入口出发，查询下一步走得通的节点，将这些可能的节点压入队列中，已经走过的节点不再尝试。查询完毕之后，从队列中取出一个节点，查询该节点周围是否存在走得通的节点。如果不存在可能的节点，就继续从队列中取一个节点。重复以上操作，直到当前节点为迷宫出口，或者队列中再无节点。如果迷宫是走得通的话，广度优先搜索会找到一条最短路径。

深度优先搜索会一直前进，直到走到死胡同为止，再回退到上一个节点，改变之前的选择。而广度优先搜索每次前进的时候，会把前后左右行得通的节点都尝试一遍，相当于每前进一个节点都要尝试多种可能，因此每次挑选的路径会是最短路径。

定义数据

• 起始节点与目标节点
• 存储节点的队列

定义辅助函数

• 获取下一节点函数 successor
• 判断是否为终点函数 test_goal

  class BreadthFirstSearch(Maze):
    def _search(self):
        queue = Queue()
        initial = self._Node(self._start, None)
        marked = {initial.state}
        queue.push(initial)
        while queue:
            parent = queue.pop()
            state = parent.state
            if self._test_goal(state):
                return parent
            children = self._success(state)
            for child in children:
                if child not in marked:
                    marked.add(child)
                    queue.push(self._Node(child, parent))