构建二叉搜索树(javascript)

二叉搜索树

二叉搜索树要求：若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值； 它的左、右子树也分别为二叉排序树。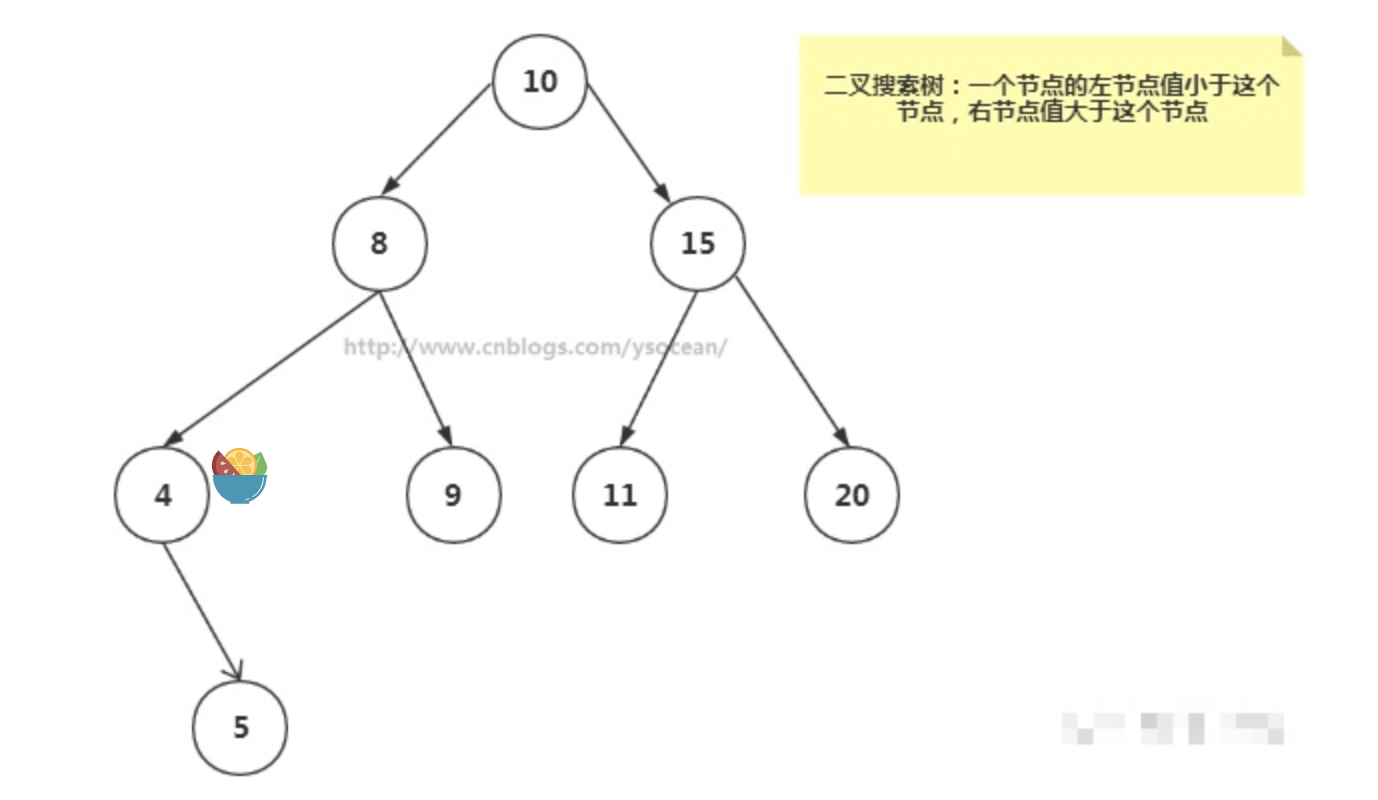

二叉搜索树节点类：

function Node (data, left, right) {
    this.data = data
    this.left = left
    this.right = right
}

现在创建一个二叉查找树(BST)，该类中只有一个表示二叉查找树根节点的Node对象，该类的构造函数将根节点初始化为null，以此创建一个空节点。

let Node = function (key) {
    this.key = key
    this.left = null
    this.right = null
  }
  let root = null

BST要有一个insert()方法，向树中添加新节点。

let insertNode = (node, newNode) => {
    if (newNode.key < node.key) {
      if (!node.left) {
        node.left = newNode
      } else {
        insertNode(node.left, newNode)
      }
    } else {
      if (!node.right) {
        node.right = newNode
      } else {
        insertNode(node.right, newNode)
      }
    }
  }

将新插入节点的值与父节点值对比，如果小，就去左子树，如果大，就去右子树。如果遇到节点的左右子树为空，就将节点插入，否则就继续向下查找。

然后遍历输入的数值，构建二叉搜索树：

this.insert = (key) => {
    let newNode = new Node (key)
    if (root === null) {
      root = newNode
    } else {
      insertNode(root, newNode)
    }
  }
  keys.forEach((key) => {
    this.insert(key)
  })
  return root
}

函数整体如下：

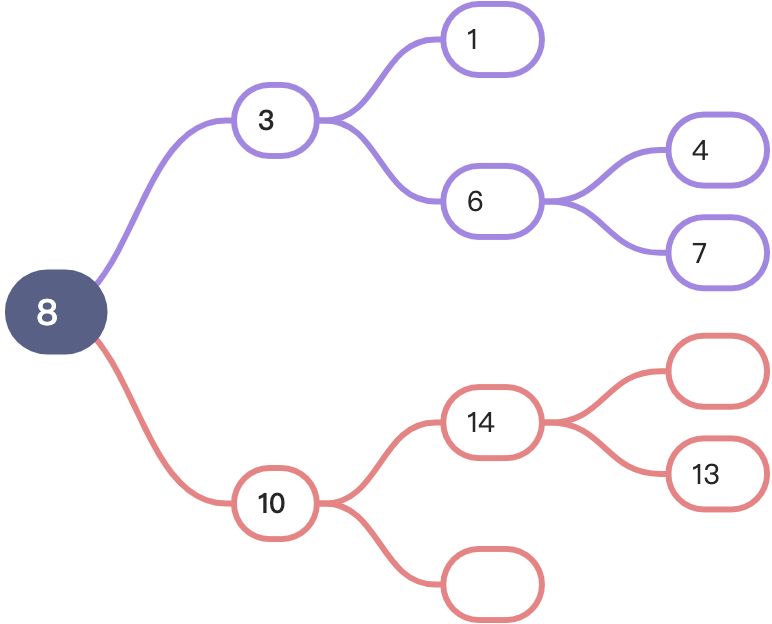
function BST(keys) {
  let Node = function (key) {
    this.key = key
    this.left = null
    this.right = null
  }
  let root = null
  let insertNode = (node, newNode) => {
    if (newNode.key < node.key) {
      if (!node.left) {
        node.left = newNode
      } else {
        insertNode(node.left, newNode)
      }
    } else {
      if (!node.right) {
        node.right = newNode
      } else {
        insertNode(node.right, newNode)
      }
    }
  }
  this.insert = (key) => {
    let newNode = new Node (key)
    if (root === null) {
      root = newNode
    } else {
      insertNode(root, newNode)
    }
  }
  keys.forEach((key) => {
    this.insert(key)
  })
  return root
}
const keys = [8,3,10,1,6,14,4,7,13]
console.log(BST(keys))

上面输出结果为：

Node {
  key: 8,
  left: Node {
    key: 3,
    left: Node { 
      key: 1, 
      left: null, 
      right: null 
    },
    right: Node { 
      key: 6, 
      left: [Node], 
      right: [Node] 
    }
  },
  right: Node {
    key: 10,
    left: null,
    right: Node { 
      key: 14, 
      left: [Node], 
      right: null 
    }
  }
}