🥈94. 二叉树的中序遍历🌱

🥈Medium

给定一个二叉树，返回它的中序遍历。
示例:

输入: [1,null,2,3]
   1
    \
     2
    /
   3
输出: [1,3,2]

进阶: 递归算法很简单，你可以通过迭代算法完成吗？

题解

递归

使用递归算法，应该很简单，竟然还写不出来！！！太垃圾了吧😧
垃圾代码：

Python

错的！

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
class Solution:
    def inorderTraversal(self, root: TreeNode) -> List[int]:
        ans=[]
        if not root:
            return ans
        if root.left:
            self.inorderTraversal(root.left)
        ans.append(root.val)
        if root.right:
            self.inorderTraversal(root.right)
        return ans

其实思路没什么问题，但添加root.val时并没有递归！

正确的！

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
class Solution:
    def inorderTraversal(self, root: TreeNode) -> List[int]:
        ans=[]
        def inorder(node):
            if not node:
                return
            inorder(node.left)
            ans.append(node.val)
            inorder(node.right)
        inorder(root)
        return ans

JavaScript

var inorderTraversal = function(root) {
    const res = [];
    const inorder = (root) => {
        if (!root) {
            return;
        }
        inorder(root.left);
        res.push(root.val);
        inorder(root.right);
    }
    inorder(root);
    return res;
};

复杂度分析

• 时间复杂度：，其中 n 为二叉树节点的个数。二叉树的遍历中每个节点会被访问一次且只会被访问一次。
• 空间复杂度：。空间复杂度取决于递归的栈深度，而栈深度在二叉树为一条链的情况下会达到 的级别。

迭代

上面递归的操作也可以用栈来完成。两种方式等价的，只不过是迭代把递归中隐式维护的栈显式模拟出来。如下图所示：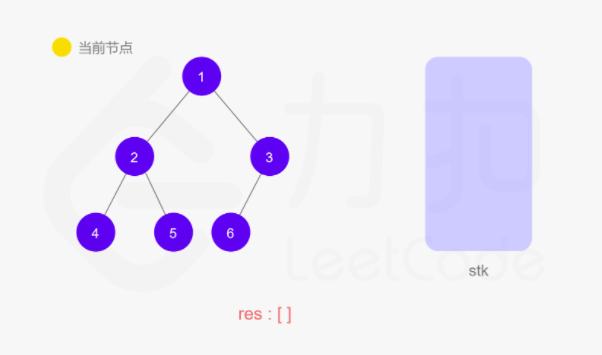

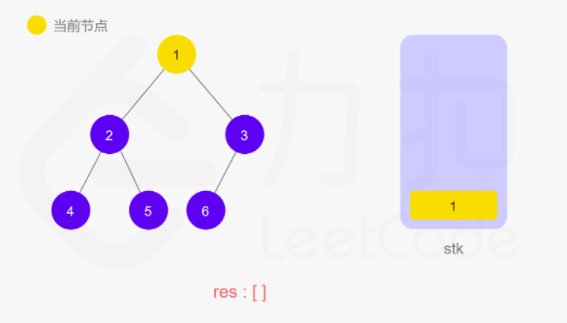
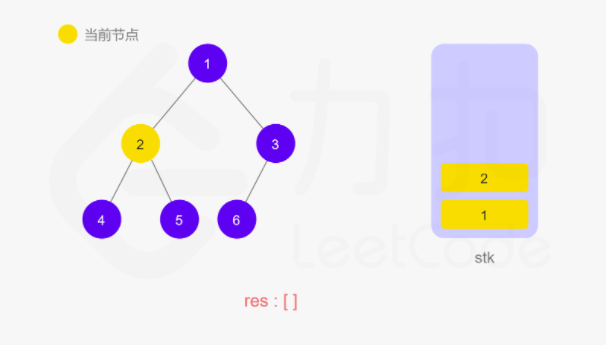
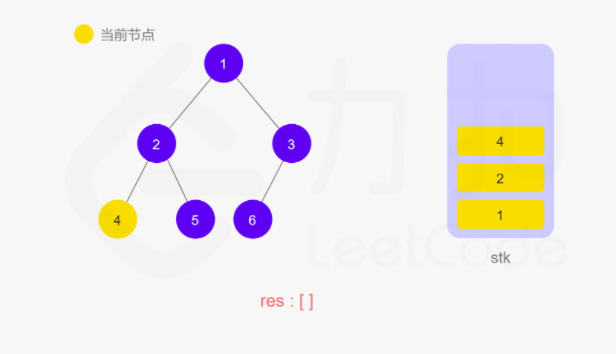
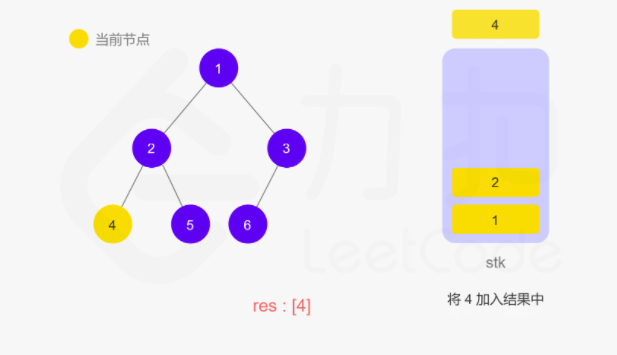
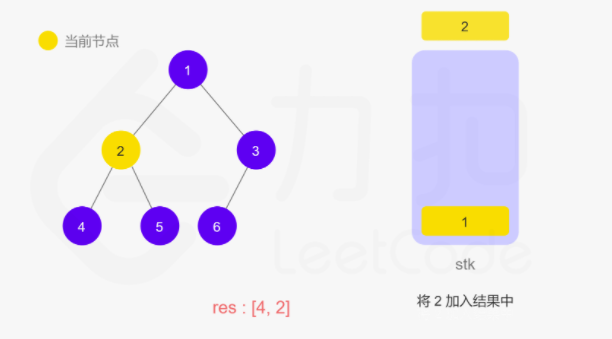
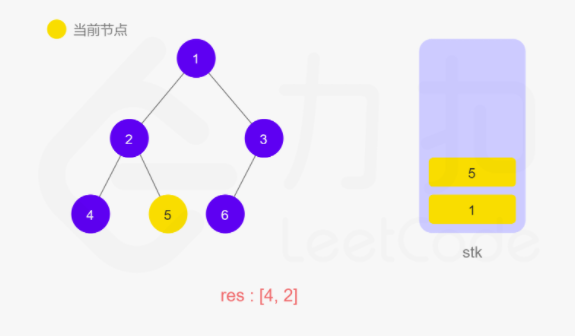
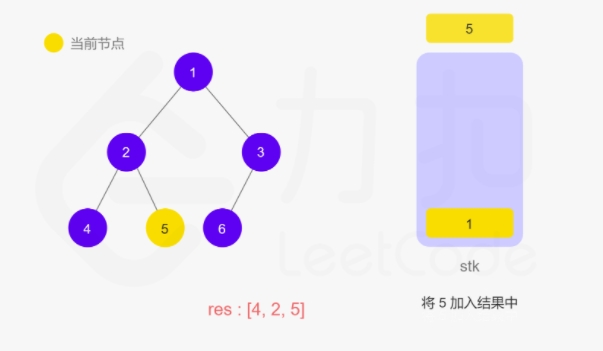
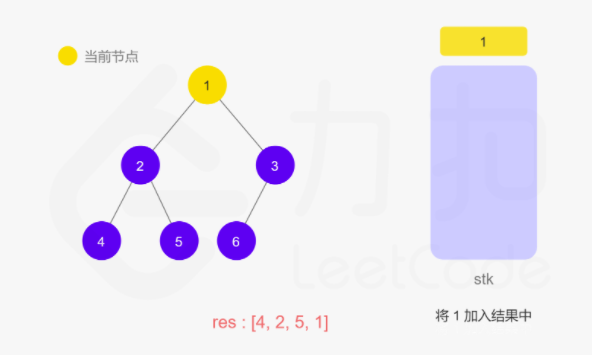
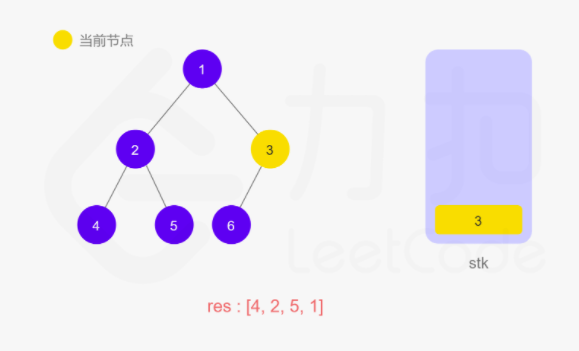
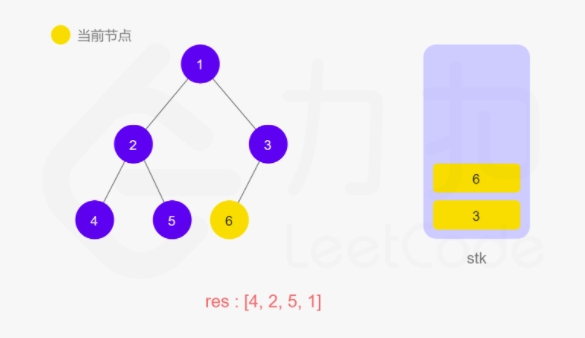
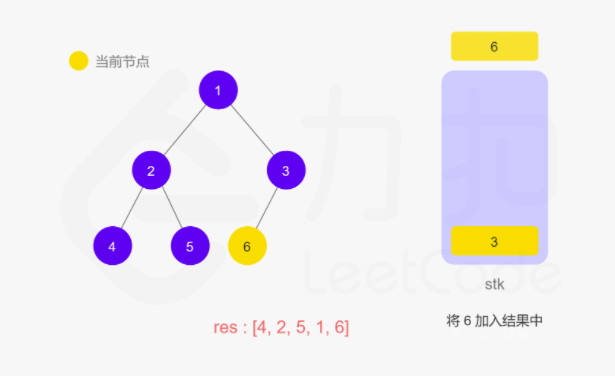
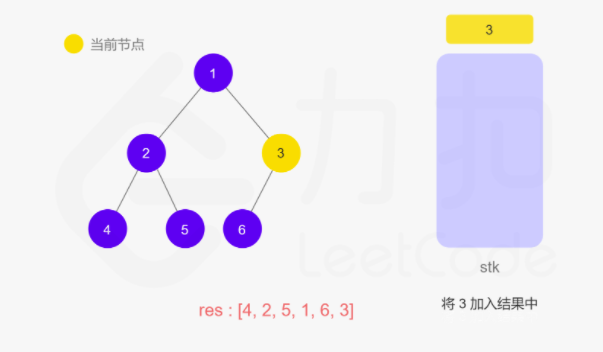
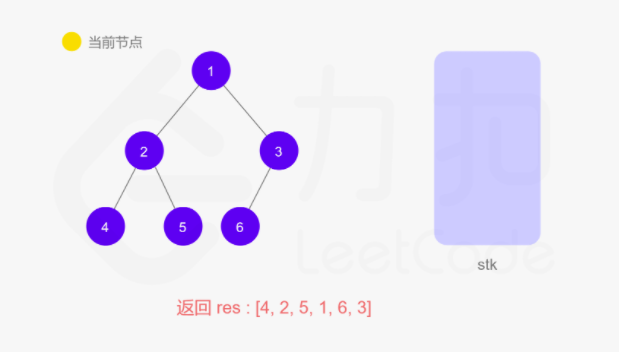
动图如下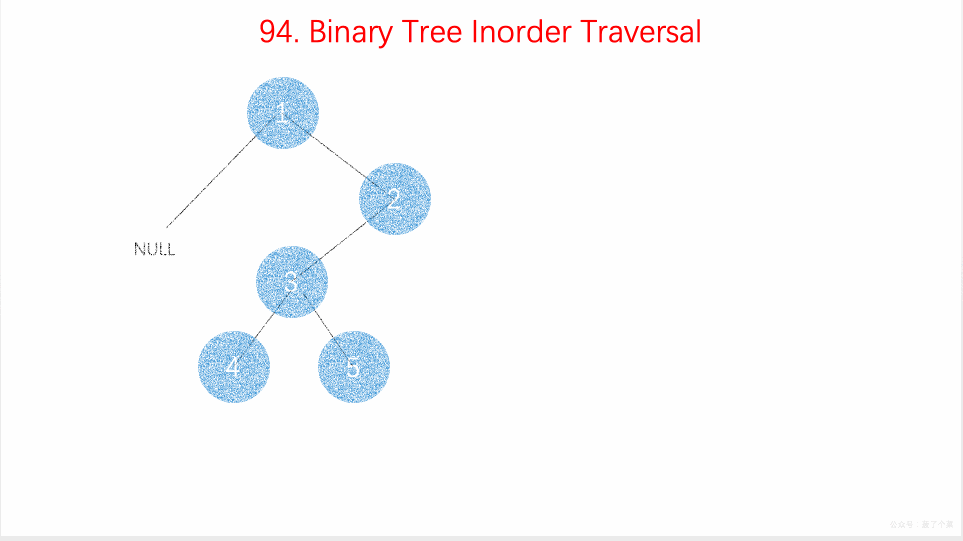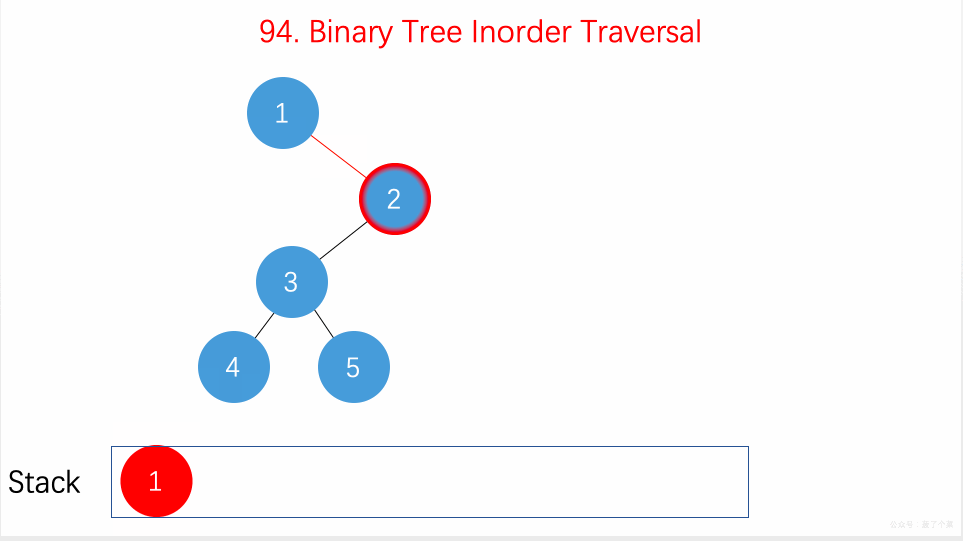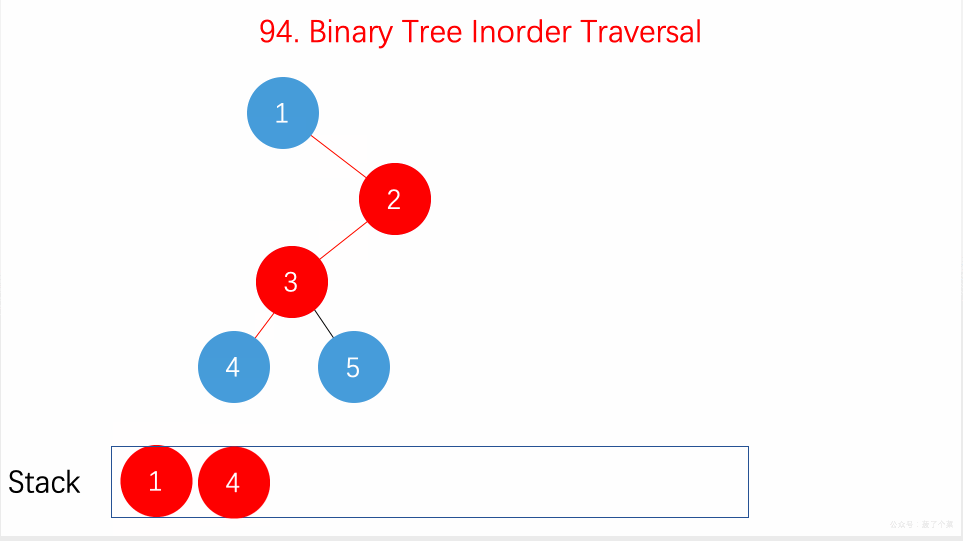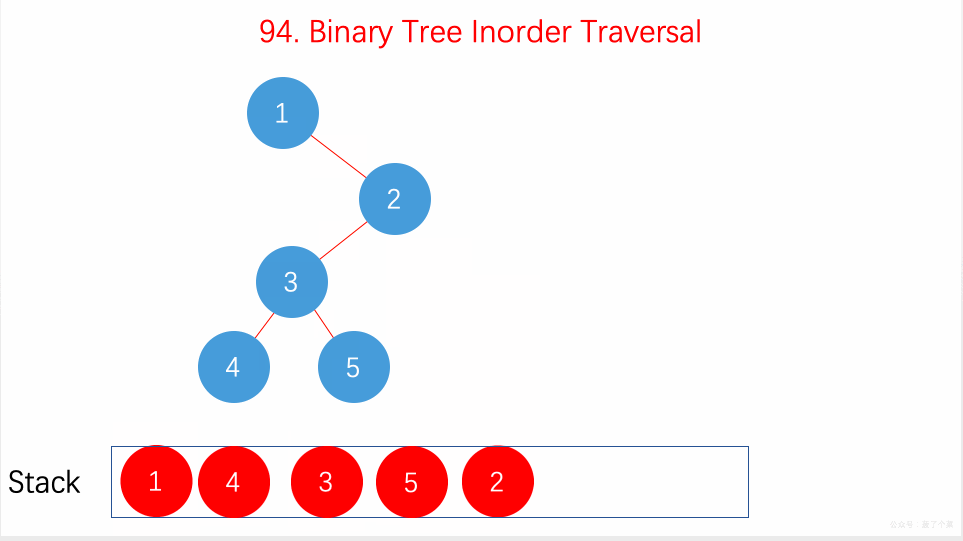

整体来说还是看节点是否有左子树，如果有就往下走，直到叶子节点，然后再返回中间结点和右子树。

Python

JavaScript

var inorderTraversal = function(root) {
    const res = [];
    const stk = [];
    while (root || stk.length) {
      // 把root节点的左子树全部加入
        while (root) {
            stk.push(root);
            root = root.left;
        }
        root = stk.pop();
        res.push(root.val);
        root = root.right;
    }
    return res;
};