深度优先搜索算法（英语：Depth-First-Search，DFS）是一种用于遍历或搜索树或图的算法。沿着树的深度遍历树的节点，尽可能深的搜索树的分支。当节点v的所在边都己被探寻过，搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点，则选择其中一个作为源节点并重复以上过程，整个进程反复进行直到所有节点都被访问为止。属于盲目搜索。深度优先搜索是图论中的经典算法，利用深度优先搜索算法可以产生目标图的相应拓扑排序表，利用拓扑排序表可以方便的解决很多相关的图论问题，如最大路径问题等等

步骤

  1. 首先将根节点放入stack中。
  2. 从stack中取出第一个节点，并检验它是否为目标。如果找到目标，则结束搜寻并回传结果。否则将它某一个尚未检验过的直接子节点加入stack中。
  3. 重复步骤2。
  4. 如果不存在未检测过的直接子节点。将上一级节点加入stack中。重复步骤2。
  5. 重复步骤4。
  6. 若stack为空，表示整张图都检查过了——亦即图中没有欲搜寻的目标。结束搜寻并回传“找不到目标”。

如下图：

image.png

基本思想

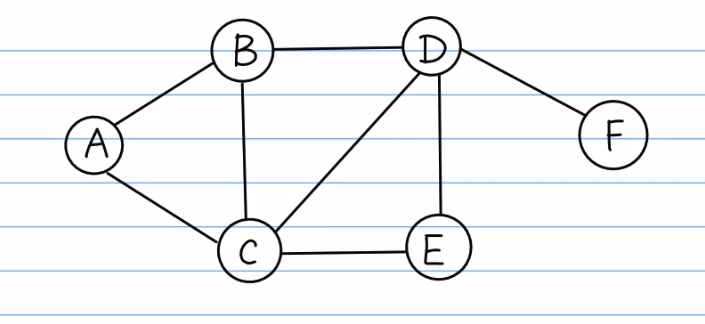
假设以A为起点,然后由A出发,访问与A邻接且未被访问的任一顶点B,再访问与B邻接且未被访问的顶点C,再访问与C邻接且未被访问的顶点E……重复上述过程.当不能再继续向下访问时,依次退回到最近被访问的顶点,若它还有邻接顶点未被访问过,则从该点开始继续上述搜索过程,直到图中所有顶点均被访问过为止.

代码

  1. def DFS(graph, s):
  2.     stack = [s]
  3.     seen = set()
  4.     seen.add(s)
  5.     while len(stack) > 0:
  6.         a = stack.pop()
  7.         nodes = graph[a]
  8.         for node in nodes:
  9.             if node not in seen:
  10.                 stack.append(node)
  11.                 seen.add(node)
  12.         print(a, end='->')