🥈medium - 🥈 1214. 查找两棵二叉搜索树之和🌱 - 《算法与LeetCode题解》

题解
- Python
- JavaScript

给出两棵二叉搜索树，请你从两棵树中各找出一个节点，使得这两个节点的值之和等于目标值 Target。
如果可以找到返回 True，否则返回 False。

示例一：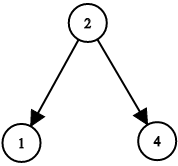

输入：root1 = [2,1,4], root2 = [1,0,3], target = 5
输出：true
解释：2 加 3 和为 5 。

示例二：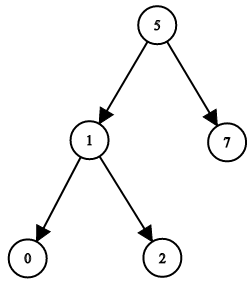

输入：root1 = [0,-10,10], root2 = [5,1,7,0,2], target = 18
输出：false

提示：

每棵树上最多有 5000 个节点。
-10^9 <= target, node.val <= 10^9

题解
虽然变成了两颗树，还是可以用遍历的方式判断两数之和是否为target，这样时间复杂度就是。
再考虑到，这里的树🌲不是普通的树，而是二叉搜索树🌱，二叉搜索树的特点是：。可以将查找的过程从变成二分，也就是遍历A树，同时B树的节点，如果和小于target，B树root=root.right，反之root=root.left，这样复杂度就是
还可以进一步优化。如果A树和B树是排好序的数组，那么求和就只需要,而将二叉搜索树变成排序数组也很简单，只需要将二叉搜索树进行中序遍历即可：

Python
```
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
 def tree2arr(self,tree):
     ans=[]
     def inorder(node):
         if not node:
             return
         inorder(node.left)
         ans.append(node.val)
         inorder(node.right)
     inorder(tree)
     return ans

 def twoSumBSTs(self, root1: TreeNode, root2: TreeNode, target: int) -> bool:
     tree1 = self.tree2arr(root1)
     tree2 = self.tree2arr(root2)
     left = 0
     right = len(tree2)-1
     while left<len(tree1) and right>=0:
         allsum = tree1[left]+tree2[right]
         if (allsum == target):
             return True
         elif (allsum > target):
             right -= 1
         else: 
             left +=1
     return False
```
JavaScript
```javascript /**
- Definition for a binary tree node.
- function TreeNode(val, left, right) {
- this.val = (val===undefined ? 0 : val)
- this.left = (left===undefined ? null : left)
- this.right = (right===undefined ? null : right)
- } / /*
- @param {TreeNode} root1
- @param {TreeNode} root2
- @param {number} target
- @return {boolean} */ function tree2list(tree){ let ans = [] const inorder = (root)=>{ if (!root) return inorder(root.left) ans.push(root.val) inorder(root.right) } inorder(tree) return ans
  } var twoSumBSTs = function(root1, root2, target) { const ans1=tree2list(root1) const ans2=tree2list(root2) let left = 0 let right = ans2.length while(left<=ans1.length && right >= 0){ let sum = ans1[left]+ans2[right] if (sum === target) return true else if (sum < target) left++ else right— } return false

}; ```

🥈 1214. 查找两棵二叉搜索树之和🌱

题解

Python

JavaScript