morris遍历可以将非递归遍历中的空间复杂度降为二叉树的Morris遍历 - 图1。从而实现时间复杂度为二叉树的Morris遍历 - 图2，而空间复杂度为二叉树的Morris遍历 - 图3 morris遍历利用的是树的叶节点左右孩子为空（树的大量空闲指针），实现空间开销的极限缩减

morris遍历的实现原则

记当前节点为**cur**

  1. 如果cur无左孩子，cur向右移动（cur=cur.right）
  2. 如果cur有左孩子，找到cur左子树上最右的节点，记为mostright
    1. 如果mostright的right指针指向空，让其指向cur，cur向左移动（cur=cur.left）
    2. 如果mostright的指针指向cur，让其指向空，cur向右移动（cur=cur.right）

实现以上原则，就实现了morris遍历

morris遍历的实质

建立一种机制，对于没有左子树的节点只到达一次，对于有左子树的节点会到达两次

morris遍历实例

一个树若按层遍历的结构为{1,2,3,4,5,6,7}，即该树为满二叉树，头结点值为1，左右孩子为2,3，叶节点为4,5,6,7

如图所示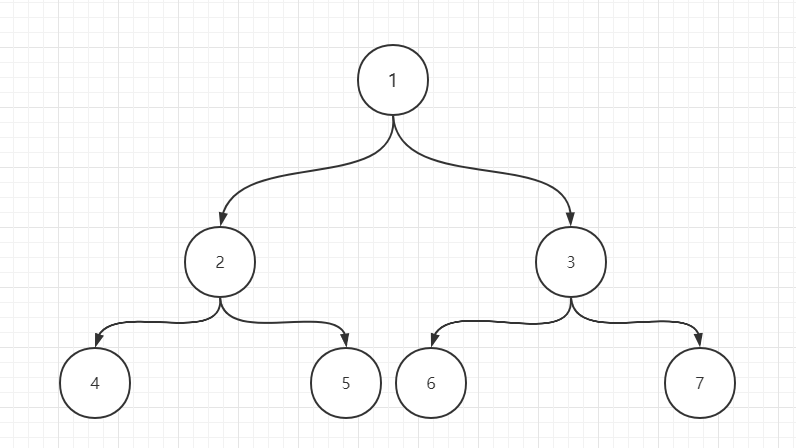
image.png

  1. cur在头结点1处，1存在左孩子，它左子树上的最右节点为5，记做mostright

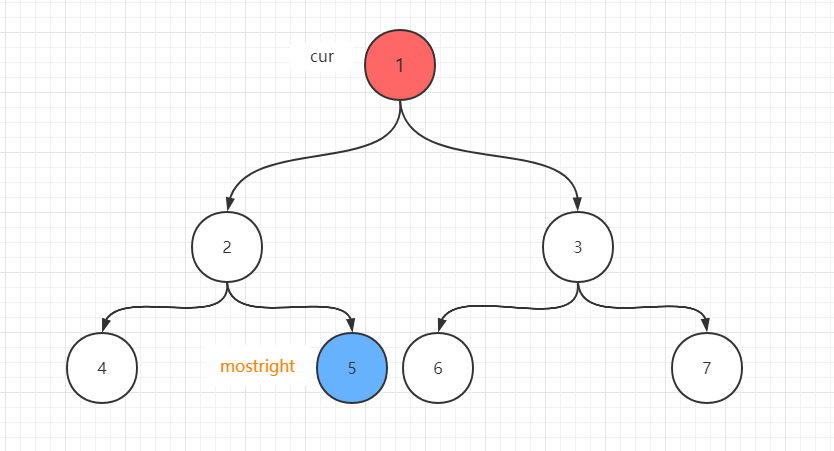
image.png

  1. mostright（5）的right指针为空，把它指向cur，此时cur要左移（cur=cur.left）,cur变成2

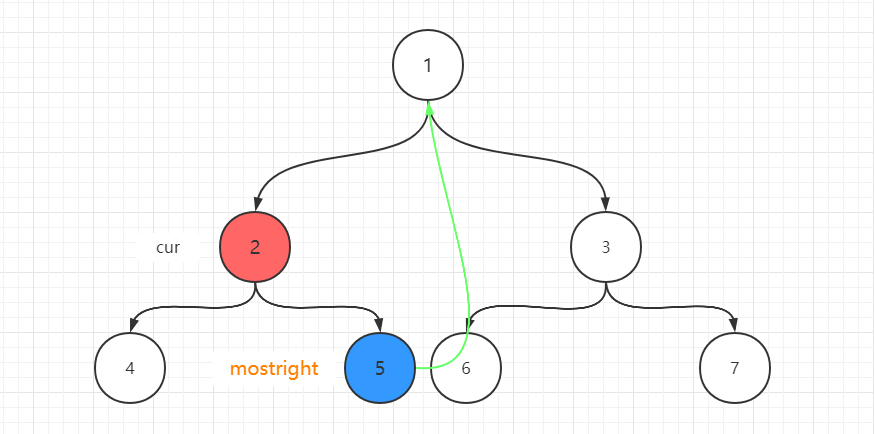
image.png

  1. 2有左孩子，它左子树上最右的点为4，且4的right指针指向空，此时mostright为4

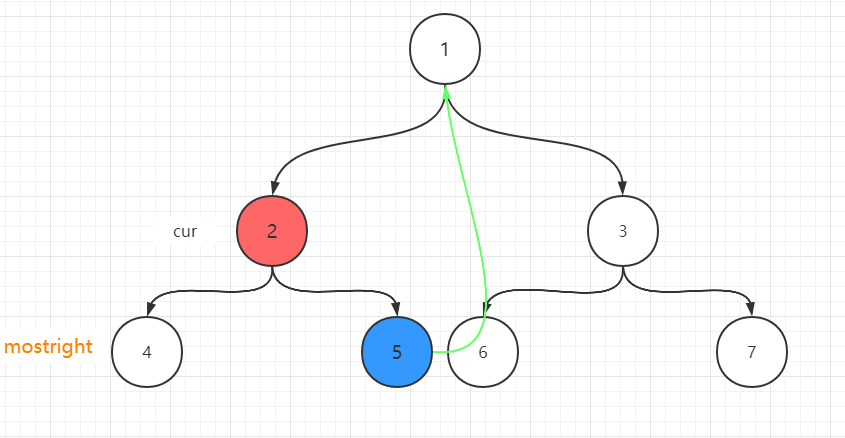
image.png

  1. 则此时要4的right指针指向当前cur（2），且cur向左移动，cur为4

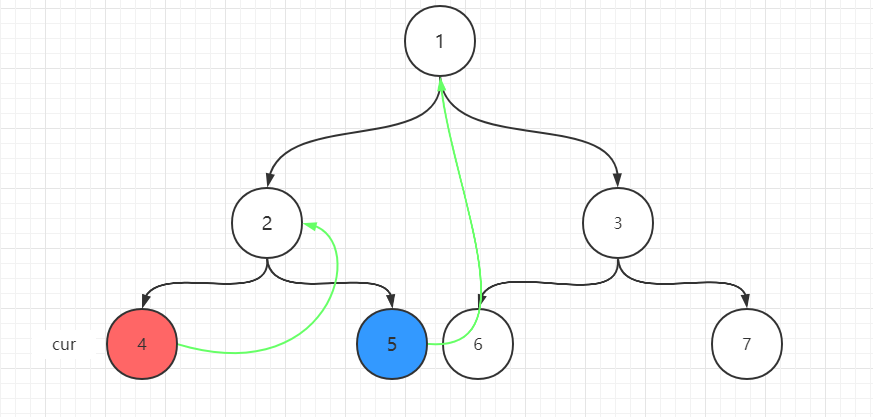
image.png

  1. 4不存在左孩子，则cur向右移动，因为cur的right指针指向了2，所以cur移动到2。

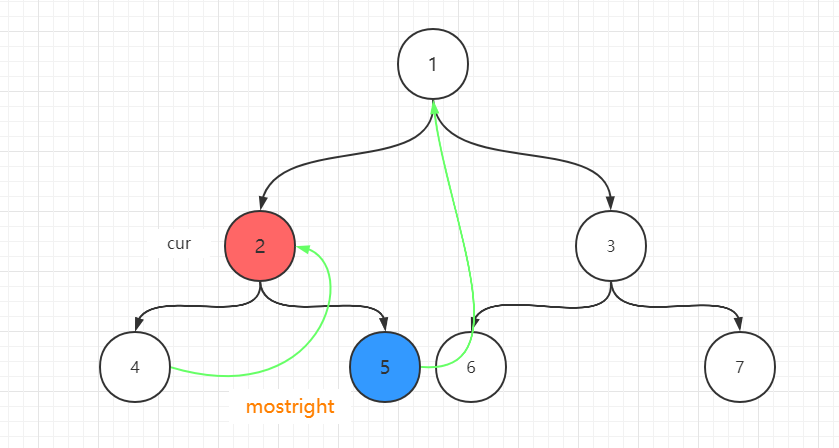
image.png

  1. 2有左孩子，它左子树上最右节点为4，但4的right指针已经指向了2，不为空。此时cur得向右移动，移动到5，同时4的right指针重新指向空

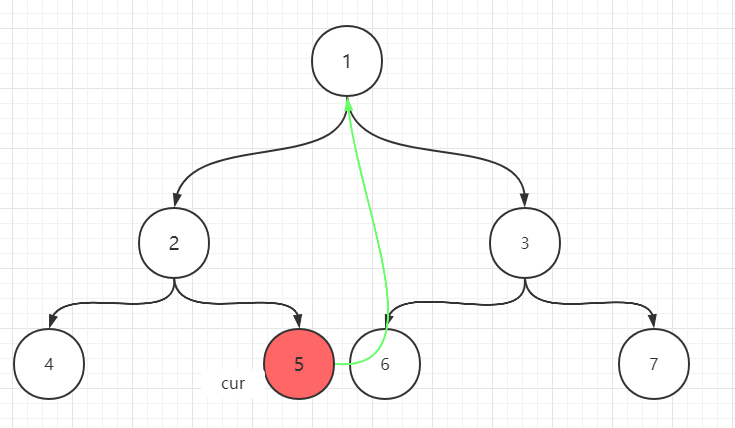
image.png

  1. 5没有左孩子，cur需要向右移动，在第2步时，5的right指针已经指向了1，所以cur又回到了1

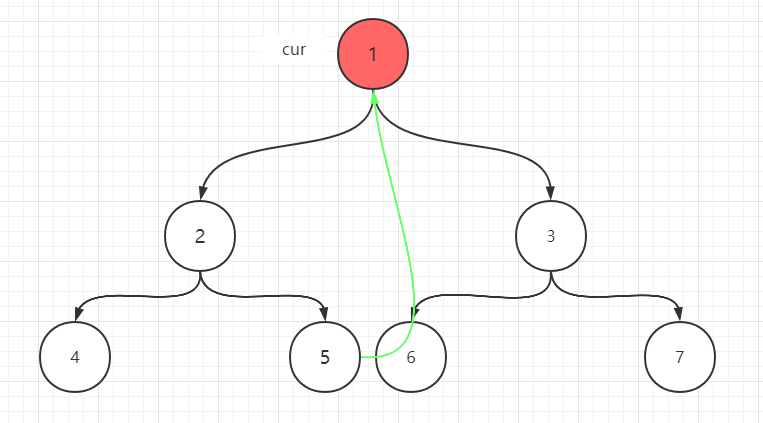
image.png

  1. cur回到1，左子树已经遍历完成了。1有左孩子，左子树最右节点为5,5的right指针指向了1，此时cur需要向右移动到3，同时5的right指针重新指向空

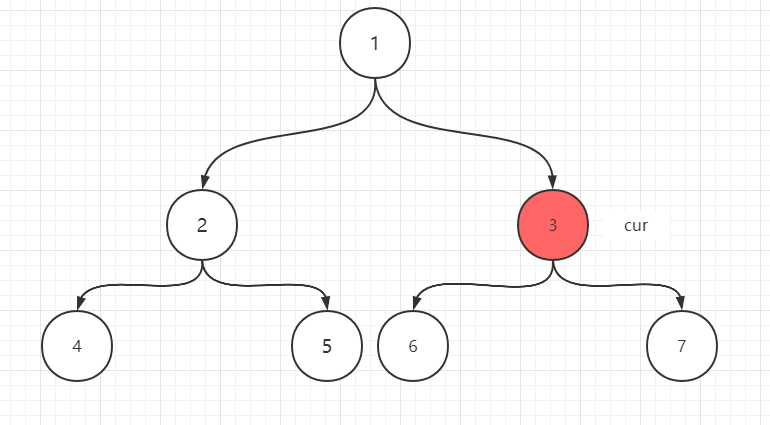
image.png

  1. 3有左孩子，3的左子树上最右的节点为6,6为mostright，6的right指针现在是空的，指向3

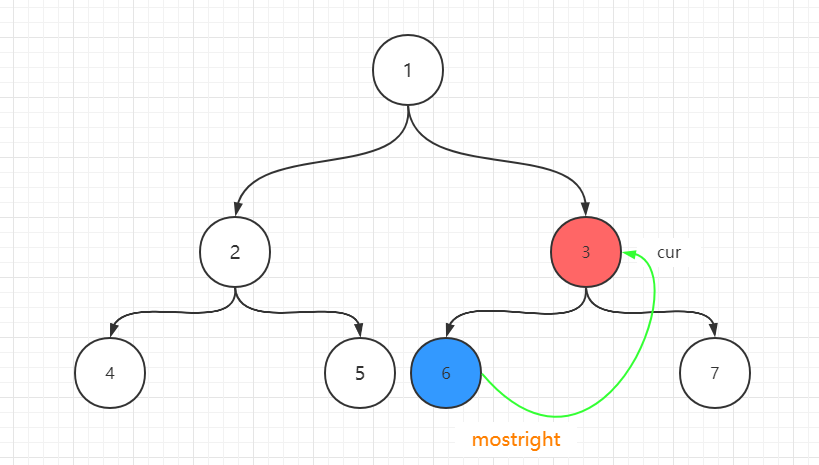
image.png

  1. cur向左移动，cur到6。

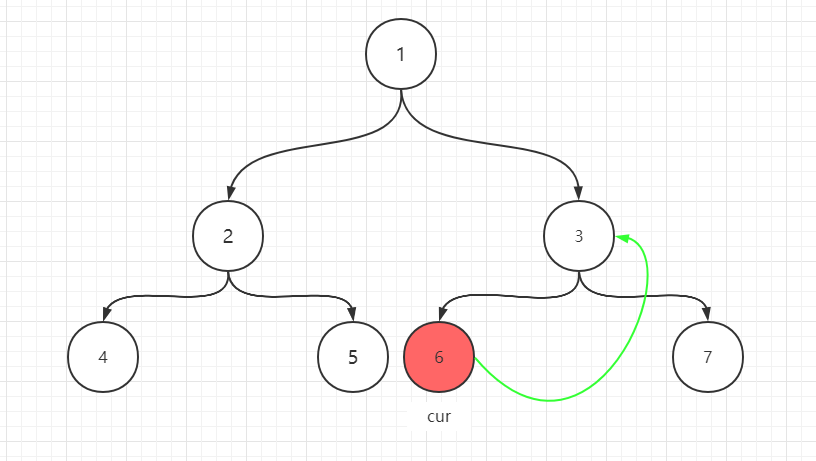
image.png

  1. 此时cur没有左孩子，cur得向右移动，6有right指针指向3，所以cur又回到了3

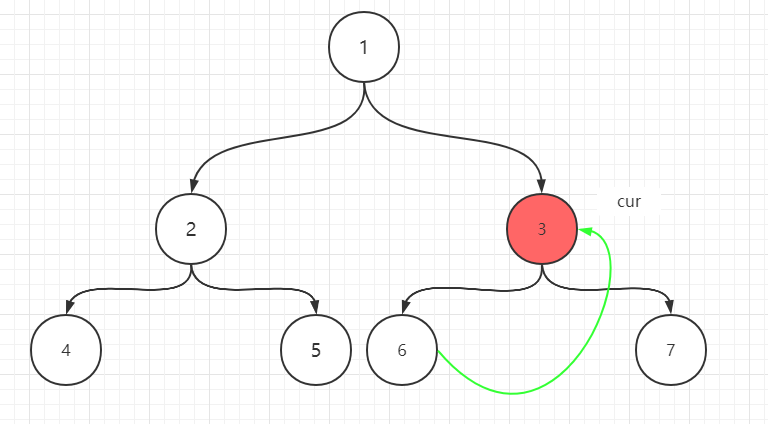
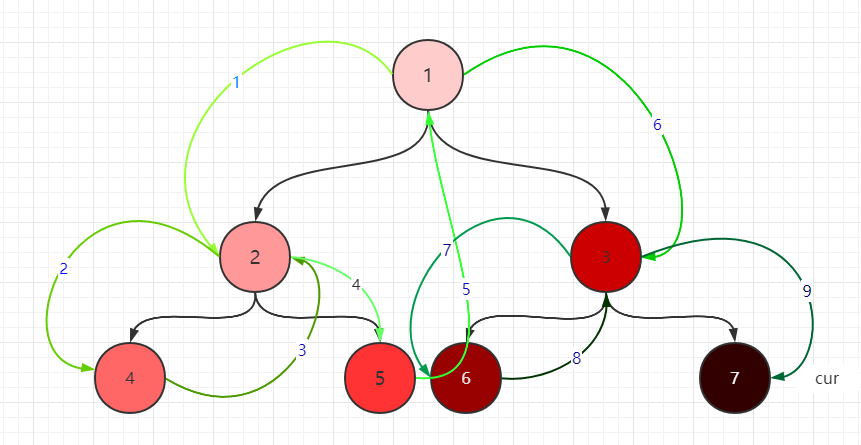
image.png
cur在3,3有左孩子6,6的right指针正指向cur，所以此时cur要右移到7，且6的right指针要变成空，这样就遍历完成了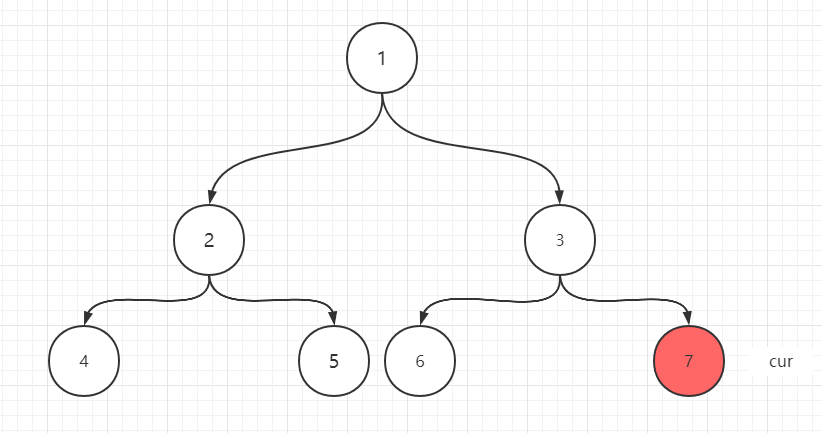
image.png

整个过程中，经过节点的顺序如下图：
1->2->4->2->5->1->3->6->3->7
image.png