🥈Medium
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。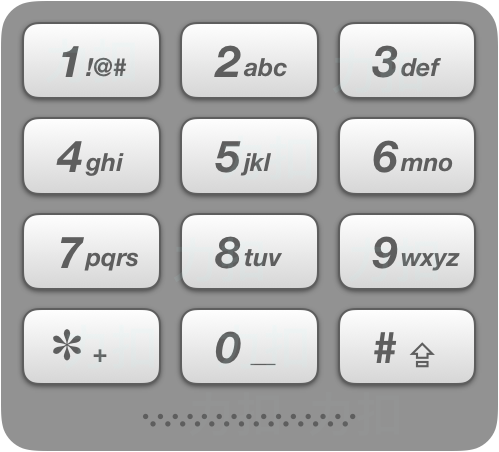
示例:
输入:"23"输出:["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].
说明:
尽管上面的答案是按字典序排列的,但是你可以任意选择答案输出的顺序。
题解
回溯(递归)
看思路我也会,但是不会写!!!😥
首先用哈希表存储每个数字对应的所有可能的字母,然后进行回溯操作。
回溯过程中要维护一个字符串,表示已有的字母排序(如果没有遍历完电话号码的所有数字,则现在的排序没有枚举完)。这个字符串开始为空,每次取电话号码的一位数字,就从哈希表中获得该数字对应的所有可能字母,并将其中一个字母插入已有的字母排列后面,然后继续处理下一位数字,直到处理完所有数字,就可以得到一个完整的字母排列。然后进行回退操作,遍历其余的字母排列。
回溯算法用于寻找所有的可行解,如果发现一个解不可行,则会舍弃不可行的解。在这道题中,由于每个数字对应的每个字母都可能进入字母组合,因此不存在不可行的解,直接穷举所有的解即可。
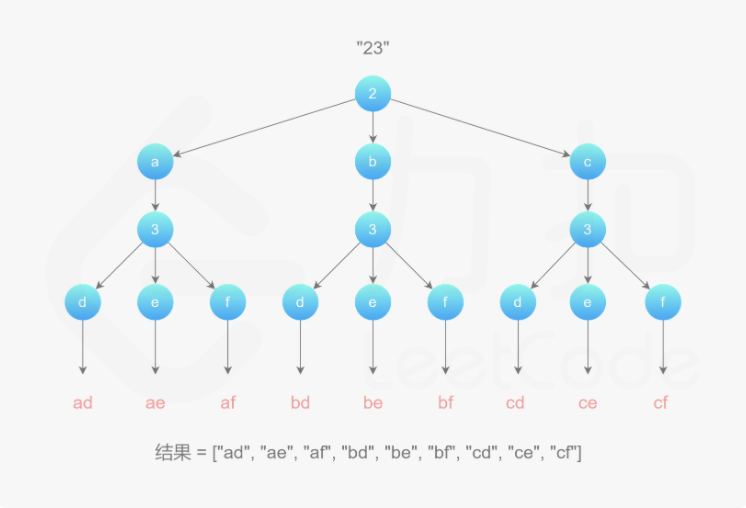
如果还不好理解,可以用下面的方式思考🤔。
假设输入的是2,因为2对应abc,所以输出的数组就是
["a","b","c"],用一个循环就解决了:ans = [] s="abc" for i in s: ans.append(i) return ans如果输入的是23,结果应该是
["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"],用二重循环就可以了:ans = [] s = 'abc' t = 'def' for i in s: for j in t: ans.append(i+j) return ans如果输入234,就变成三重循环了,也就是说输入的字符串长度为n,整个遍历就有n重。但由于n不确定,循环的嵌套层数也不固定,此时就需要递归。
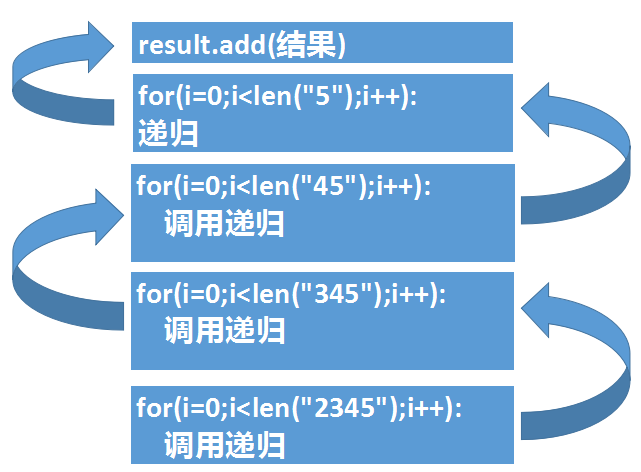
- 对于打印”2345”这样的字符串:
- 第一次递归就是上图中最下面的方格,然后处理完第一个字符2之后,将输入的字符改变成”345”并调用第二个递归函数
- 第二次递归处理3,将字符串改变成”45”后再次递归
- 第三次递归处理4,将字符串改变成”5”后继续递归
- 第四次递归处理5,将字符串改变成””后继续递归
- 最后发现字符串为空了,将结果放到列表中并返回
上面是从函数调用的角度去看的,而每次调用下一层递归时,都需要将本层的一些处理结果放到一个临时变量中,再传递给下一层,从这个变量层层传递的变化看,就像一棵树一样,这个算法的时间复杂度很高,是O(3^n)这个级别的,空间复杂度是O(n)
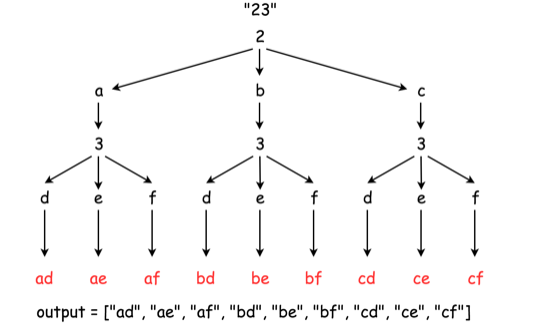
Python
def letterCombinations(digits):
if not digits:
return list()
phoneMap = {
'2': 'abc',
'3': 'def',
'4': 'ghi',
'5': 'jkl',
'6': 'mno',
'7': 'pqrs',
'8': 'tuv',
'9': 'wxyz'
}
combination = []
combinations = []
def backtrack(index):
if index == len(digits):
# 如果遍历到数字列表中最后一个说明遍历完成了,将整个列表整合成字符串放到结果列表中
combinations.append(''.join(combination))
else:
digit = digits[index]
for letter in phoneMap[digit]:
combination.append(letter)
backtrack(index + 1)
combination.pop()
backtrack(0) # 从第一个index开始遍历
return combinations
# >>> "23"
# <<< ["ad","ae","af","bd","be","bf","cd","ce","cf"]
代码思路如下:
以输入的"23"为例
从输入的第一个数2开始,遍历对应的哈希表{2:abc},然后遍历abc,将a先加入combination中,即[a],然后再backtrack(index + 1),也就是追踪3,再从3对应的哈希表{3:def},继续遍历,就可以将d加入combination中,combination就变成了[a,d],现在index已经等于len(digits),combination已经完成了,将其转成字符串"ad",d就完成自己的使命了,从combination中弹出。
然后接着从e继续……整个就类似于深度优先的遍历
JavaScript
/**
* @param {string} digits
* @return {string[]}
*/
var letterCombinations = function(digits) {
if(!digits){
return []
}
phoneMap = {
'2': 'abc',
'3': 'def',
'4': 'ghi',
'5': 'jkl',
'6': 'mno',
'7': 'pqrs',
'8': 'tuv',
'9': 'wxyz'
}
let temp=[]
let ans=[]
var backtrack = function (index) {
if (index === digits.length) {
ans.push(temp.join(''))
} else {
let digit = digits[index]
for(let key of phoneMap[digit]){
temp.push(key)
backtrack(index+1)
temp.pop()
}
}
}
backtrack(0)
return ans
};
复杂度分析
时间复杂度:
.其中 m 是输入中对应 3 个字母的数字个数(包括数字 2、3、4、5、6、8),nn 是输入中对应 4 个字母的数字个数(包括数字 7、9),m+n 是输入数字的总个数。当输入包含 m 个对应 3 个字母的数字和 n 个对应 4 个字母的数字时,不同的字母组合一共有
种,需要遍历每一种字母组合。
空间复杂度:
,其中 m 是输入中对应 3 个字母的数字个数,n 是输入中对应 4 个字母的数字个数,m+n 是输入数字的总个数。除了返回值以外,空间复杂度主要取决于哈希表以及回溯过程中的递归调用层数,哈希表的大小与输入无关,可以看成常数,递归调用层数最大为 m+n。

