二叉搜索树

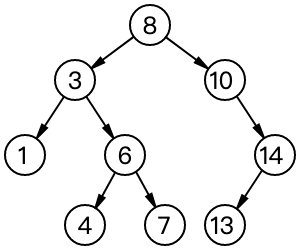
二叉查找树（英语：Binary Search Tree），也称为 二叉搜索树、有序二叉树（Ordered Binary Tree）或排序二叉树（Sorted Binary Tree），是指一棵空树或者具有下列性质的二叉树：

• 若任意节点的左子树不空，则左子树上所有节点的值均小于它的根节点的值；
• 若任意节点的右子树不空，则右子树上所有节点的值均大于它的根节点的值；
• 任意节点的左、右子树也分别为二叉查找树；
• 没有键值相等的节点。

二叉查找树相比于其他数据结构的优势在于查找、插入的时间复杂度较低。为 。二叉查找树是基础性数据结构，用于构建更为抽象的数据结构，如集合、多重集、关联数组等。

二叉查找树的查找过程和次优二叉树类似，通常采取二叉链表作为二叉查找树的存储结构。中序遍历二叉查找树可得到一个关键字的有序序列，一个无序序列可以通过构造一棵二叉查找树变成一个有序序列，构造树的过程即为对无序序列进行查找的过程。每次插入的新的结点都是二叉查找树上新的叶子结点，在进行插入操作时，不必移动其它结点，只需改动某个结点的指针，由空变为非空即可。搜索、插入、删除的复杂度等于树高，期望 ，最坏 （数列有序，树退化成线性表）。

虽然二叉查找树的最坏效率是 ，但它支持动态查询，且有很多改进版的二叉查找树可以使树高为 ，从而将最坏效率降至 ，如 AVL 树、红黑树等。