Trie，音同try，又叫字典树、前缀树、单词查找树。用于检索字符串数据集中的键。

应用场景

此数据结构有多种应用：

  1. 自动补全

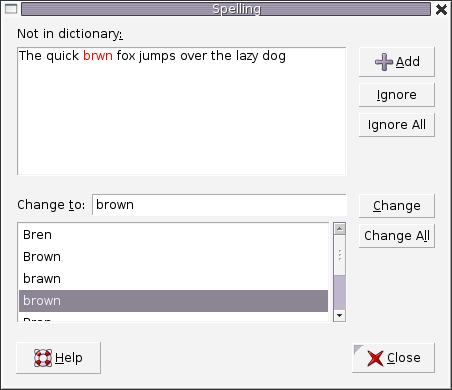
image.png

  1. 拼写检查

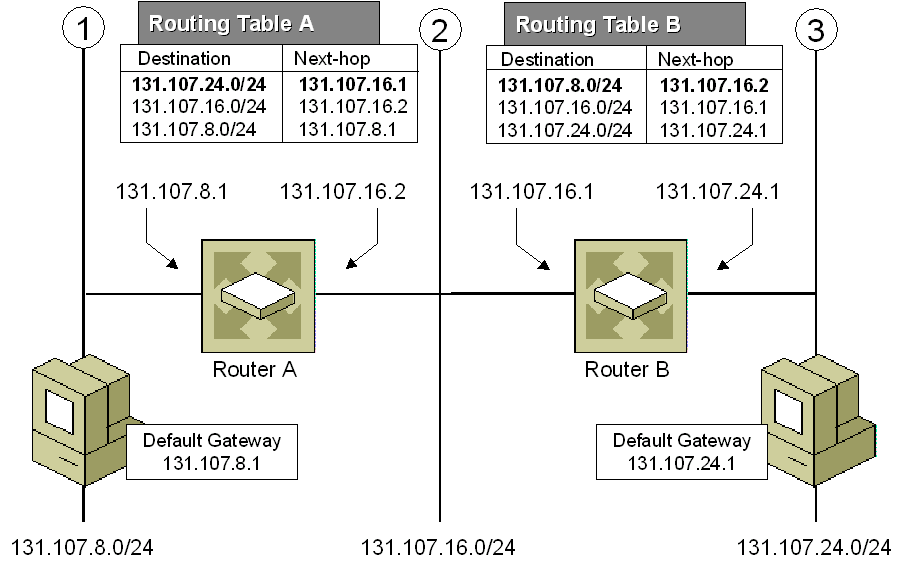
image.png

  1. IP路由（最长前缀匹配）

image.png

  1. 九宫格输入法打字预测

image.png

优点

还有其他的数据结构，如平衡树和哈希表，能够在字符串数据集中搜索单词。为什么我们还需要 Trie 树呢？尽管哈希表可以在 🌳字典树(Trie) - 图5间内寻找键值，却无法高效的完成以下操作：

  • 找到具有同一前缀的全部键值。
  • 按词典序枚举字符串的数据集。

Trie 树优于哈希表的另一个理由是，随着哈希表大小增加，会出现大量的冲突，时间复杂度可能增加到 🌳字典树(Trie) - 图6，其中 n 是插入的键的数量。与哈希表相比，Trie 树在存储多个具有相同前缀的键时可以使用较少的空间。此时 Trie 树只需要 🌳字典树(Trie) - 图7的时间复杂度，其中 m 为键长。而在平衡树中查找键值需要 🌳字典树(Trie) - 图8时间复杂度。

Trie树的结构

Trie 树是一个有根的树，其结点具有以下字段：

  • 最多 R 个指向子结点的链接，其中每个链接对应字母表数据集中的一个字母（假定 R 为 26，小写拉丁字母的数量）。
  • 布尔字段，以指定节点是对应键的结尾还是只是键前缀。

如下图是单词leet在Trie树中的表示：
image.png

向Trie树中插入键

通过搜索 Trie 树来插入一个键。从根开始搜索它对应于第一个键字符的链接。有两种情况：

  • 链接存在。沿着链接移动到树的下一个子层。算法继续搜索下一个键字符。
  • 链接不存在。创建一个新的节点，并将它与父节点的链接相连，该链接与当前的键字符相匹配。

重复以上步骤，直到到达键的最后一个字符，然后将当前节点标记为结束节点，算法完成。如图所示，将三个单词(le、leet、code)构造Trie树：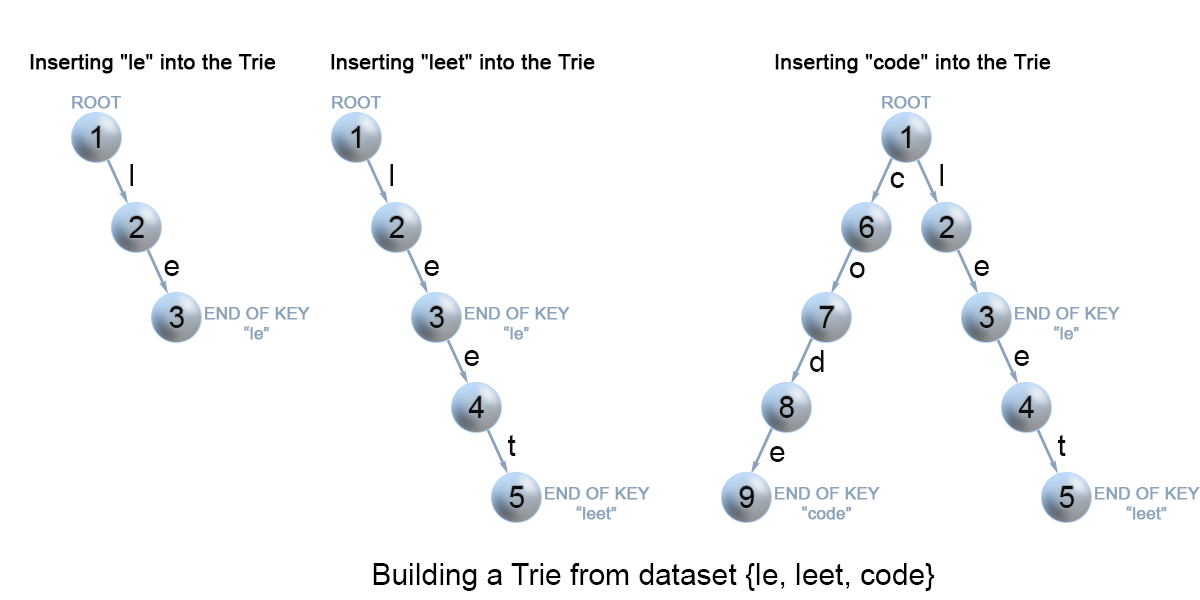
image.png

复杂度分析

  • 时间复杂度：🌳字典树(Trie) - 图11，其中 m 为键长。在算法的每次迭代中，我们要么检查要么创建一个节点，直到到达键尾。只需要 m 次操作。

  • 空间复杂度：🌳字典树(Trie) - 图12。最坏的情况下，新插入的键和 Trie 树中已有的键没有公共前缀。此时需要添加 m 个结点，使用 🌳字典树(Trie) - 图13空间。

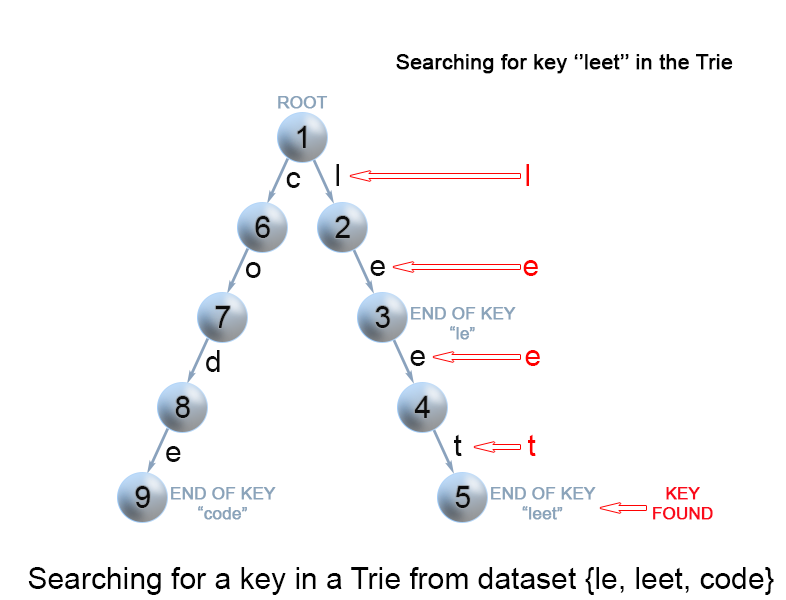
在Trie树中查找键

每个键在 trie 中表示为从根到内部节点或叶的路径。用第一个键字符从根开始，检查当前节点中与键字符对应的链接。有两种情况：

  • 存在链接。移动到该链接后面路径中的下一个节点，并继续搜索下一个键字符。
  • 不存在链接。若已无键字符，且当前结点标记为 isEnd，则返回 true。否则有两种可能，均返回 false :
    • 还有键字符剩余，但无法跟随 Trie 树的键路径，找不到键。
    • 没有键字符剩余，但当前结点没有标记为 isEnd。也就是说，待查找键只是Trie树中另一个键的前缀。

如图是在上面构建的Trie树上查找leet：
image.png

复杂度分析

  • 时间复杂度：🌳字典树(Trie) - 图15。算法每一步都要搜索下一个键字符。最坏情况需要m次操作

  • 空间复杂度：🌳字典树(Trie) - 图16

    查找Trie树中的键前缀

    该方法与在 Trie 树中搜索键时使用的方法非常相似。从根遍历 Trie 树，直到键前缀中没有字符，或者无法用当前的键字符继续 Trie 中的路径。与上面提到的“搜索键”算法唯一的区别是，到达键前缀的末尾时，总是返回 true。我们不需要考虑当前 Trie 节点是否用 “isend” 标记，因为搜索的是键的前缀，而不是整个键。例如，下面是查找前缀co：
    image.png

    复杂度分析

  • 时间复杂度：🌳字典树(Trie) - 图18

  • 空间复杂度：🌳字典树(Trie) - 图19

代码实现

Python

  1. class Node:
  2.     def __init__(self):
  3.         self.child = [None for _ in range(26)]
  4.         self.isEnd = False
  6.     def contain_key(self,ch):
  7.         return self.child[ord(ch)-ord('a')]
  9.     def get(self,ch):
  10.         return self.child[ord(ch)-ord('a')]
  12.     def put(self,ch):
  13.         self.child[ord(ch)-ord('a')] = Node()
  16. class Trie:
  18.     def __init__(self):
  19.         """
  20.         Initialize your data structure here.
  21.         """
  22.         self.root = Node()
  24.     def insert(self, word: str) -> None:
  25.         """
  26.         Inserts a word into the trie.
  27.         """
  28.         p = self.root
  29.         for i in word:
  30.             if not p.contain_key(i):
  31.                 p.put(i)
  32.             p = p.get(i)
  33.         p.isEnd = True
  35.     def search(self, word: str) -> bool:
  36.         """
  37.         Returns if the word is in the trie.
  38.         """
  39.         p = self.root
  40.         for i in word:
  41.             if not p.contain_key(i):
  42.                 return False
  43.             else:
  44.                 p = p.get(i)
  45.         return p.isEnd
  48.     def startsWith(self, prefix: str) -> bool:
  49.         """
  50.         Returns if there is any word in the trie that starts with the given prefix.
  51.         """
  52.         p = self.root
  53.         for i in prefix:
  54.             if not p.contain_key(i):
  55.                 return False
  56.             else:
  57.                 p = p.get(i)
  58.         return True
  61. # Your Trie object will be instantiated and called as such:
  62. # obj = Trie()
  63. # obj.insert(word)
  64. # param_2 = obj.search(word)
  65. # param_3 = obj.startsWith(prefix)

JavaScript

/**
 * Initialize your data structure here.
 */
var TrieNode = function (val) {
  // 当前节点的值
  this.val = val
  // 当前节点是否为某个单词的最后一个字母，若是，则代表是一个单词
  this.isWord = false
  // 子节点
  this.children = new Map()
}

var Trie = function() {
  this.root = new TrieNode(null)
};

/**
 * Inserts a word into the trie. 
 * @param {string} word
 * @return {void}
 */
Trie.prototype.insert = function(word) {
  let cur = this.root
  const len = word.length
  // 将单词插入到树中
  for (let i = 0; i < len; i++) {
    const char = word[i]
    if (!cur.children.has(char)) {
      cur.children.set(char, new TrieNode(char))
    }
    cur = cur.children.get(char)
    // 遍历到结尾的时候将 isWord 设为 true
    if (i === len - 1) {
      cur.isWord = true
    }
  }
};

/**
 * Returns if the word is in the trie. 
 * @param {string} word
 * @return {boolean}
 */
Trie.prototype.search = function(word) {
  let cur = this.root
  for (let char of word) {
    // 如果该字符不在 children 中，说明是新单词
    if (!cur.children.has(char)) {
      return false
    }
    cur = cur.children.get(char)
  }
  // 若顺利遍历完该单词，则进行判断该单词最后一个字母所在节点的 isWord 是否为真
  // 因为存在 key(未插入) / keyword(已插入) 这种情况
  return cur.isWord
};

/**
 * Returns if there is any word in the trie that starts with the given prefix. 
 * @param {string} prefix
 * @return {boolean}
 */
Trie.prototype.startsWith = function(prefix) {
  // 与 search 方法相比，该方法只需要判断能否成功遍历所有字符
  let cur = this.root
  for (let char of prefix) {
    if (!cur.children.has(char)) {
      return false
    }
    cur = cur.children.get(char)
  }
  return true
};