⛳️ 动态规划

方法

动态规划问题一般形式是求最值，

• 求解动态规划的核心是穷举。但穷举时会存在重复子问题，如果暴力穷举，效率会很低下，需要“备忘录”来优化穷举过程，避免不必要的计算。
• 动态规划问题一定具备最优子结构，这样才能通过子问题的最值得到原问题的最值
• 只有列出状态转移方程，才能正确穷举

写出状态方程，一定要注意以下几点：

• 这个情况的base case（最简单情况）是什么
• 这个问题有什么状态
• 对于每个状态，可以做出什么选择使得状态改变
• 如何定义dp数组（函数）的含义表示状态和选择

关键就是：状态、选择、dp数组的定义，代码可以套下面的框架：

# 初始化base case
dp[0][0][...] = base case
# 进行状态转移
for 状态1 in 状态1所有值:
    for 状态2 in 状态2所有值:
        for ...:
            dp[状态1][状态2][...] = max(选择1,选择2,...)

举个🌰子

斐波那契数列

暴力递归

利用斐波那契数列的通项公式：

def fib(n):
    if n == 0:
        return 0
    elif n == 1 or n == 2:
        return 1
    return fib(n - 1) + fib(n - 2)

这样虽然简单，但是效率很低，如果n=20，递归树如图（遇到递归问题，最好画出递归树，这有利于分析算法复杂度）：

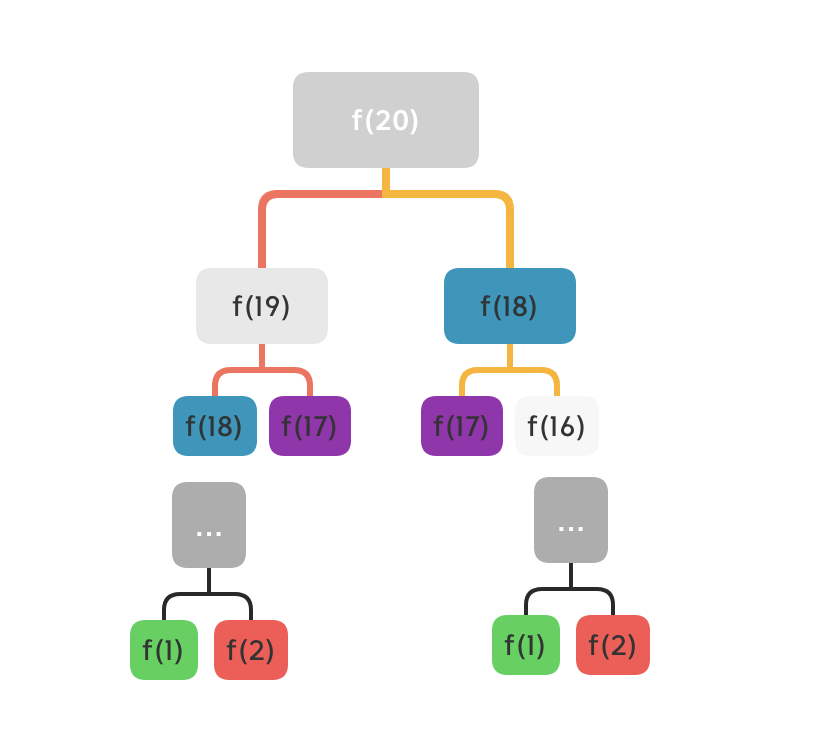
从上图可以看到，要计算，就得先计算和，….,直到或。

递归算法的时间复杂度就是用子问题的个数*解决一个子问题所需的时间。
**
暴力方法中，很显然子问题的个数就是递归树节点的个数，也就是个。解决一个子问题的时候，没有循环，只有和相加，时间复杂度为。所以暴力递归的时间复杂度为。

观察递归树，可以发现算法低效的原因是存在着大量的重复计算（图中同色部分）。这就是动态规划的第一个性质：重复子问题。需要想办法解决。

📝 带备忘录的递归解法

既然耗时的原因是重复计算，那我们就可以在计算出某个子问题的答案时，先记录再返回。每次遇到子问题先查询备忘录，如果之前已经解决了，直接拿出答案，就不用再去计算了。

一般都是使用数组作为备忘录，哈希表（字典）也可以。

上面的暴力递归可以改写为：

def fib(n):
    if n == 0:
        return 0
    memo = [0] * (n + 1)
    return helper(memo, n)


def helper(memo, n):
    if n == 1 or n == 2:
        memo[n] = 1
        return 1
    if memo[n] != 0:
        return memo[n]
    memo[n] = helper(memo, n-1) + helper(memo, n-2)
    print(memo)
    return memo[n]

同样，画出递归树的备忘录，可以看到带了备忘录之后，把一棵带有大量冗余的树做了剪枝，变成了不存在冗余的递归图，极大地减少了子问题的个数。

因为本算法不存在冗余，所以子问题为，时间复杂度也是。比起暴力递归，时间复杂度减小了好多。

但这种解法是自顶而下的，而动态规划是自底向上的，这使得动态规划一般脱离了递归，由循环迭代完成计算。

dp数组迭代解法

在上面备忘录的基础上，可以把备忘录独立出来变成一张表，在此表上完成自底向上的推算：

def fib(n):
    if n == 0:
        return 0
    if n == 1 or n == 2:
        return 1
    dp = [0] * (n + 1)
    dp[1] = dp[2] = 1
    for i in range(3, n + 1):
        dp[i] = dp[i - 1] + dp[i - 2]
    return dp[n]

如图所示：

可以看到这样的解法和带备忘录的递归一致，只不过是反过来计算了。

描述动态规划有状态转移方程，就是描述问题结构的数学形式，它是解决动态规划问题的核心。本题的状态转移方程为：

能够发现，状态转移方程代表着暴力解法。但最困难的就是写出写出暴力解法（状态转移方程），优化无非是备忘录或者dp table。

状态压缩

由上面的状态转移方程可知，当前状态只和之前的两个状态相关，不需要一个很长的数组存储所有状态。所以可以进一步优化，把空间复杂度从变成。

def fib(n):
    if n == 0:
        return 0
    if n == 1 or n == 2:
        return 1
    prev = curr = 1
    for i in range(3, n + 1):
        sum = prev + curr
        prev = curr
        curr = sum
    return curr

这就是状态压缩。如果每次状态转移只需要dp table中的一部分，那么就可以尝试缩小dp table的大小，只记录必要的数据。