🥈304. 二维区域和检索 - 矩阵不可变

🥈Medium

给定一个二维矩阵，计算其子矩形范围内元素的总和，该子矩阵的左上角为 (row1, col1) ，右下角为 (row2, col2) 。

上图子矩阵左上角 (row1, col1) = (2, 1) ，右下角(row2, col2) = (4, 3)，该子矩形内元素的总和为 8。

示例：

给定 matrix = [
[3, 0, 1, 4, 2],
[5, 6, 3, 2, 1],
[1, 2, 0, 1, 5],
[4, 1, 0, 1, 7],
[1, 0, 3, 0, 5]
]
sumRegion(2, 1, 4, 3) -> 8
sumRegion(1, 1, 2, 2) -> 11
sumRegion(1, 2, 2, 4) -> 12

提示：

• 你可以假设矩阵不可变。
• 会多次调用 sumRegion 方法。
• 你可以假设 row1 ≤ row2 且 col1 ≤ col2 。

题解

此题就是303的二维化：
🥉303. 区域和检索 - 数组不可变
303，因为是一维，用暴力一次时间复杂度为，但变成二维之后，一次暴力时间复杂度就变成，不太可取。同样需要前缀和进行优化。

一维前缀和

初始化的时候，对矩阵的每一行计算前缀和，检索时对二维区域中每一行计算子数组和，然后对每一行的子数组和计算总和

具体实现方面，创建 行列的二维数组，其中 和 分别是矩阵 的行数和列数，为 的前缀和数组。将 的列数设为 的目的是为了方便计算每一行的子数组和，不需要对 的情况特殊处理。

Python

class NumMatrix:
    def __init__(self, matrix: List[List[int]]):
        m, n = len(matrix), (len(matrix[0]) if matrix else 0)
        self.sums = [[0] * (n + 1) for _ in range(m)]
        _sums = self.sums

        for i in range(m):
            for j in range(n):
                _sums[i][j + 1] = _sums[i][j] + matrix[i][j]

    def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:
        _sums = self.sums

        total = sum(_sums[i][col2 + 1] - _sums[i][col1] for i in range(row1, row2 + 1))
        return total

JavaScript

var NumMatrix = function(matrix) {
    const m = matrix.length;
    if (m > 0) {
        const n = matrix[0].length;
        this.sums = new Array(m).fill(0).map(() => new Array(n + 1).fill(0));
        for (let i = 0; i < m; i++) {
            for (let j = 0; j < n; j++) {
                this.sums[i][j + 1] = this.sums[i][j] + matrix[i][j];
            }
        }
    }
};

NumMatrix.prototype.sumRegion = function(row1, col1, row2, col2) {
    let sum = 0;
    for (let i = row1; i <= row2; i++) {
        sum += this.sums[i][col2 + 1] - this.sums[i][col1];
    }
    return sum;
};

复杂度分析

• 时间复杂度：初始化 ，每次检索 ，其中 和分别是矩阵的行数和列数。初始化需要遍历矩阵 计算二维前缀和，时间复杂度是 。每次检索需要对二维区域中的每一行计算子数组和，二维区域的行数不超过 ，计算每一行的子数组和的时间复杂度是 ，因此每次检索的时间复杂度是。
• 空间复杂度：，其中 和 分别是矩阵的行数和列数。需要创建一个行 列的前缀和数组 。

二维前缀和

👆上面的方法虽然用了前缀和，但每次检索时间复杂度为，有没有办法降到呢？

也就只能用二维前缀和了！

设和分别是矩阵的行数和列数。定义当且时，为矩阵的以为右下角的子矩阵元素之和：

或时，计算只需要对矩阵最上边的行和最左边的列分别计算前缀即可。但且时，就不是那么好计算了。但如果知道、和就容易多了：

具体推导如下：

所以初始化的时候，就可以对所有和计算出
示意图如下：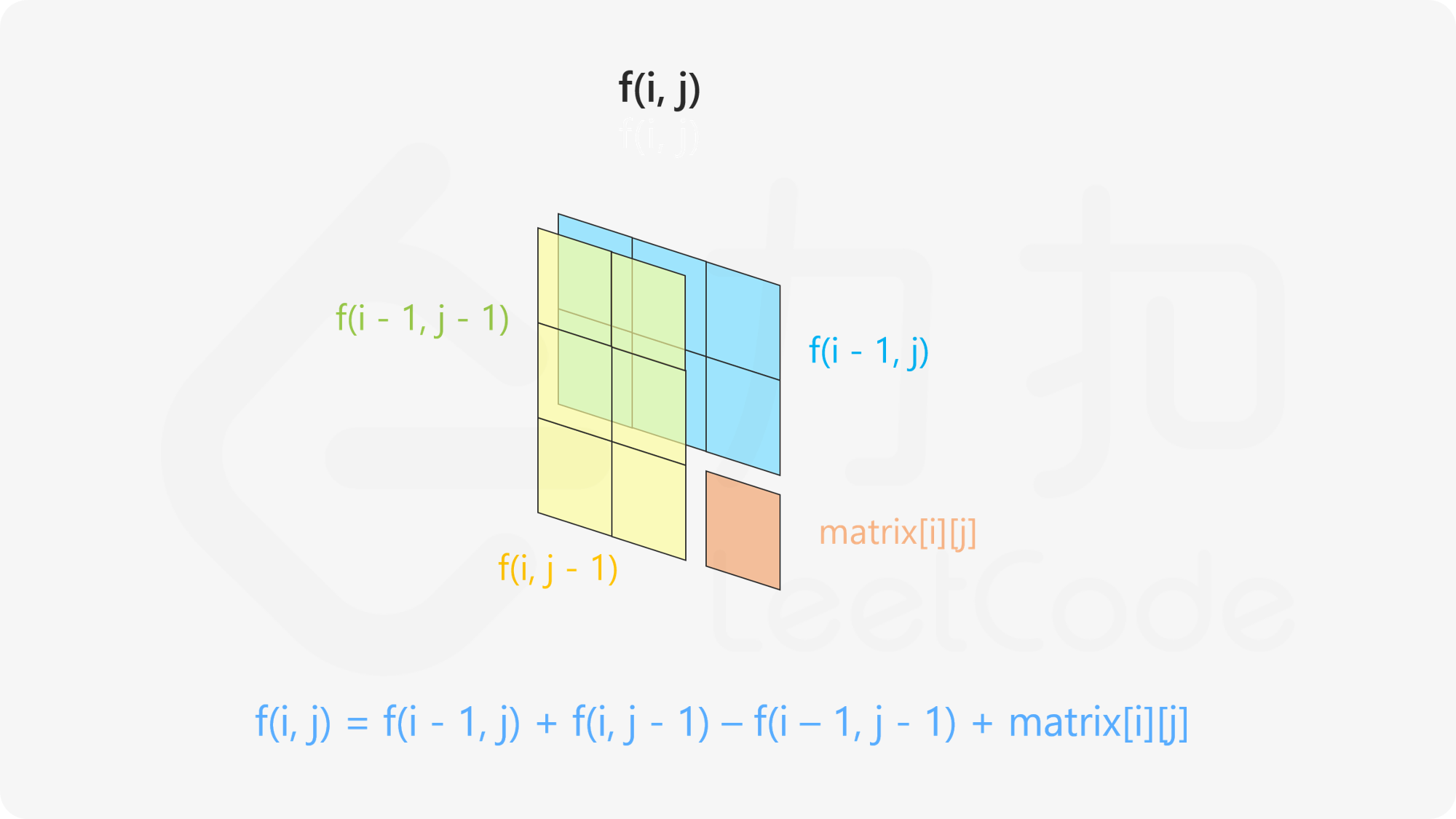

所以和一维前缀和一样，创建行列的二维数组 sums，其中 的值为的值。

将sums 的行数和列数分别设为和的目的是为了方便计算 ，不需要对和的情况特殊处理。此时有：

Python

class NumMatrix:

    def __init__(self, matrix: List[List[int]]):
        m, n = len(matrix), (len(matrix[0]) if matrix else 0)
        self.sums = [[0] * (n + 1) for _ in range(m + 1)]
        _sums = self.sums

        for i in range(m):
            for j in range(n):
                _sums[i + 1][j + 1] = _sums[i][j + 1] + _sums[i + 1][j] - _sums[i][j] + matrix[i][j]

    def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:
        _sums = self.sums

        return _sums[row2 + 1][col2 + 1] - _sums[row1][col2 + 1] - _sums[row2 + 1][col1] + _sums[row1][col1]

JavaScript

/**
 * @param {number[][]} matrix
 */
var NumMatrix = function(matrix) {
    const m = matrix.length
    if (m > 0) {
        let n = matrix[0].length
        this.sums = new Array(m+1).fill(0).map(()=> new Array(n+1).fill(0))
        for(let i=0;i<m;i++){
            for(let j=0;j<n;j++){
                this.sums[i+1][j+1] = this.sums[i][j+1]+this.sums[i+1][j]-this.sums[i][j]+matrix[i][j]
            }
        }
    }
};

/**
 * @param {number} row1
 * @param {number} col1
 * @param {number} row2
 * @param {number} col2[


 * @return {number}
 */
NumMatrix.prototype.sumRegion = function(row1, col1, row2, col2) {
    return this.sums[row2+1][col2+1]-this.sums[row1][col2+1]-this.sums[row2+1][col1]+this.sums[row1][col1]

};

复杂度分析

• 时间复杂度：初始化 ，每次检索 ，其中 和 分别是矩阵 的行数和列数。初始化需要遍历矩阵计算二维前缀和，时间复杂度是。每次检索的时间复杂度是 。

• 空间复杂度：，其中 和 分别是矩阵 的行数和列数。需要创建一个行 列的二维前缀和数组 。