🥈Medium

给定两个整数 n 和 k，返回 1 … n 中所有可能的 k 个数的组合。
示例:

  1. 输入: n = 4, k = 2
  2. 输出:
  3. [
  4.   [2,4],
  5.   [3,4],
  6.   [2,3],
  7.   [1,2],
  8.   [1,3],
  9.   [1,4],
  10. ]

题解

一看就是枚举的题目，有点思路，还是不会哦😨

慢慢来，多想多练！这也是一道回溯法的经典题目。

回溯法

还是一步一步来，示例给了 n = 4, k = 2，每一个结果数组中肯定都是两个元素，所以只需要二重for循环即可：

let n = 4
for (let i=0; i<=n; i++){
    for(let j=i+1; j<=n; j++){
      ans.push([i,j])
  }
}

同样的，如果k变成3，就会是三重循环。如果k是50、100，就很难循环了。此时就需要回溯法了：

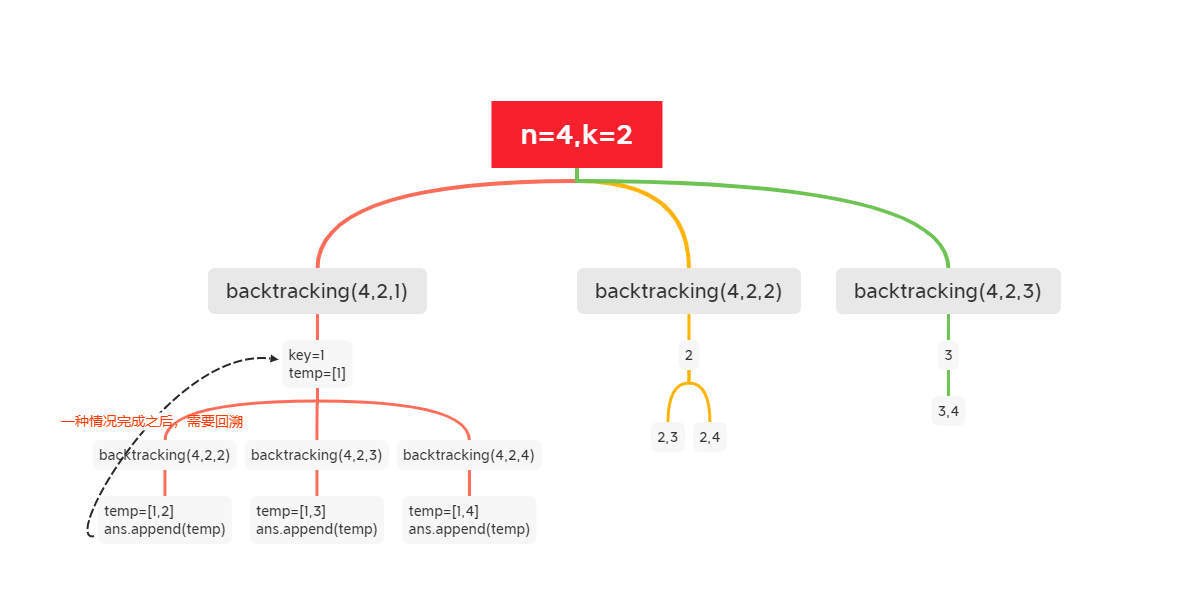
整个过程可以抽象成一个树状结构：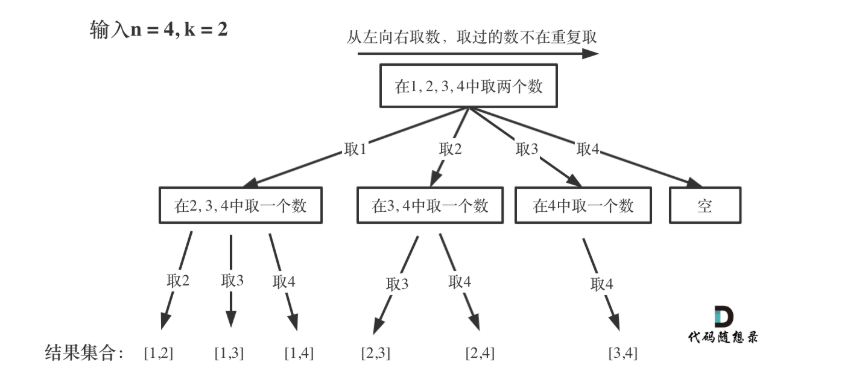
image.png
可以看到，一开始集合是 1，2，3，4， 从左向右去数，取过的数，不在重复取。

第一取1，集合变为2，3，4 ，因为k为2，我们只需要去一个数就可以了，分别取，2，3，4， 得到集合[1,2] [1,3] [1,4]，以此类推。

当每次搜索到了叶子节点，我们就找到了一个结果，就可以把它加入结果数组中。

回溯算法大体框架如下：

backtracking() {
    if (终止条件) {
        存放结果;
    }

    for (选择：选择列表（可以想成树中节点孩子的数量）) {
        递归，处理节点;
        backtracking();
        回溯，撤销处理结果
    }
}

其实backtracking就是向下（向叶子节点）遍历，而for是横向遍历（遍历这一层所有的节点），这样就把这棵树遍历完了。

Python

def combine(n,k):
    ans=[]
    temp=[]
    if k==0 or k>n:
        return ans
    def backtracking(n,k,index):
        if len(temp)==k:
            ans.append(temp[:]) # 浅拷贝一定要加，因为这里是浅拷贝，直接添加temp，后续temp值会发生改变
            return
        for key in range(index,n+1):
            temp.append(key)
            backtracking(n,k,key+1)
            temp.pop()
    backtracking(n,k,1)
    return ans

其中，backtracking函数的含义是：如果temp中元素个数已经是k个，说明已经满足条件了，把temp加入ans即可。如果不满足，就需要在[index,n]的闭区间上遍历。加入一个值后，就在下一层遍历。

比如n=4，k=2。遍历时从1开始，把1加入temp。之后往下递归，执行backtracking(4,2,2)，把2加入temp，然后要执行backtracking(4,2,3)，但现在len(temp)==2，ans需要将[1,2]加入，这样一次遍历就完成了。

[1,2]完成，但1开头的组合还有，就需要把2pop出来，让3、4继续加入遍历。

    def backtracking(n,k,index):
        if len(temp)==k:
            ans.append(temp[:])
            return
        for key in range(index,n+1):
            temp.append(key)
            backtracking(n,k,key+1)
            temp.pop()

示意图如下：
image.png

JavaScript

/**
 * @param {number} n
 * @param {number} k
 * @return {number[][]}
 */
var combine = function(n, k) {
    let ans=[]
    if(k===0 || k>n){
        return ans
    }
    let temp=[]
    function backtracting(n,k,index){
        if(temp.length===k){
            ans.push(temp.slice())
            return 
        }
        for(let i=index;i<=n;i++){
            temp.push(i)
            backtracting(n,k,i+1)
            temp.pop()
        }

    }
    backtracting(n,k,1)
    return ans

};

Java

import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Deque;
import java.util.List;

public class Solution {

    public List<List<Integer>> combine(int n, int k) {
        List<List<Integer>> res = new ArrayList<>();
        if (k <= 0 || n < k) {
            return res;
        }

        // 为了防止底层动态数组扩容，初始化的时候传入最大长度
        Deque<Integer> path = new ArrayDeque<>(k);
        dfs(1, n, k, path, res);
        return res;
    }

    private void dfs(int begin, int n, int k, Deque<Integer> path, List<List<Integer>> res) {
        if (k == 0) {
            res.add(new ArrayList<>(path));
            return;
        }

        // 基础版本的递归终止条件：if (begin == n + 1) {
        if (begin > n - k + 1) {
            return;
        }
        // 不选当前考虑的数 begin，直接递归到下一层
        dfs(begin + 1, n, k, path, res);

        // 不选当前考虑的数 begin，递归到下一层的时候 k - 1，这里 k 表示还需要选多少个数
        path.addLast(begin);
        dfs(begin + 1, n, k - 1, path, res);
        // 深度优先遍历有回头的过程，因此需要撤销选择
        path.removeLast();
    }
}

参照位运算

位运算时，每个位置都有两个状态0和1，在这里也可以参照位运算的表示方式，每个数字都有选与不选两个状态。如图：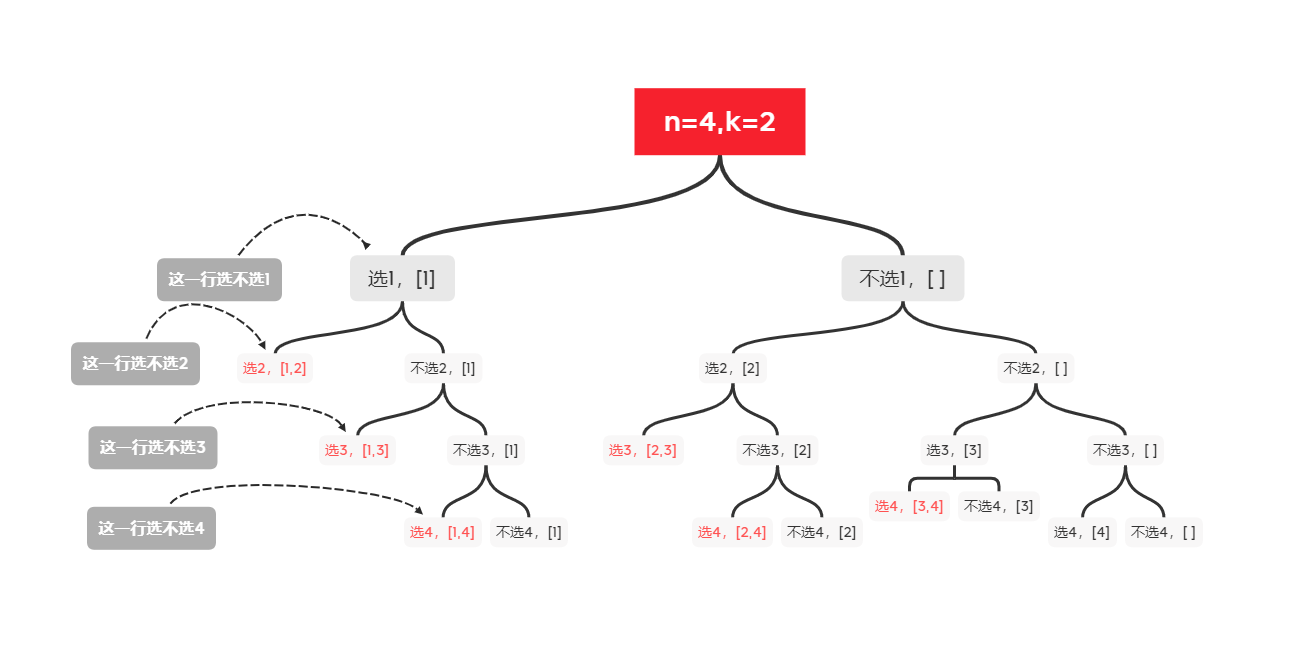
image.png
代码和上面差不多

利用组合公式进行递归

高中数学中，有🥈77. 组合 - 图4,于是就有了很简洁的写法：

class Solution(object):
    def combine(self, n, k):
        if k>n or k==0:
            return []
        if k==1:
            return [[i] for i in range(1,n+1)]
        if k==n:
            return [[i for i in range(1,n+1)]]

        answer=self.combine(n-1,k)
        for item in self.combine(n-1,k-1):
            item.append(n)
            answer.append(item)

        return answer