我们可以把整张 Network 想象成一个物理仿真系统 (Simulation)。系统中的每个节点 (Node) 都是一个带有能量的粒子，粒子与粒子之间存在斥力（如模拟库伦斥力），而被边 (Link) 所连结的粒子受到牵引力（如模拟胡克弹力）。系统中的粒子在斥力和引力的不断作用下，从随机无序的布局 (Layout) 不断发生位移，逐渐趋于平衡有序的布局。同时整个仿真系统的能量也在不断消耗，经过数次迭代后，粒子之间不再发生相对位移，整个系统达到最终稳定平衡的状态。
    力导向图中的力 - 图1
    此动效实现的本质就是每一帧都重新渲染图中节点的位置 (x,y)，节点的位置 (x,y) 是由节点上一帧所处的位置 (x,y) + 速度 (vx,vy) 所决定的，而速度就是通过力学模型所计算出来的。

    关键在于力(Forces)，D3 中内置了几种经典的力模型。

    中心力
    中心力可以使得节点最终布局是围绕着某个中心的。相当于某个中心点对所有的节点都有一个制约，不会让布局的中心偏离。

    碰撞力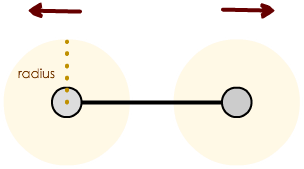
    力导向图中的力 - 图2

    • 碰撞力为每个节点都设定一个圆形的碰撞区域，从而防止节点之间重叠；
    • 关键参数：radius 碰撞半径。

    牵引力（Links）
    力导向图中的力 - 图3

    • 牵引力的强度与节点之间的距离成正比，类似于弹簧力；
    • 关键参数：distance。影响两个节点之间的最终距离。

    N 体力(Many-Body)
    N体问题是天体力学的一种力学模型，它研究 N 个质点相互之间在万有引力作用下的运动规律。

    • Many-Body 力是作用于所有节点之间的，是全局的，任何两个节点之间都将受到此力的影响。（与 牵引力 Links 不同，Links 力仅仅会影响有连接关系的两个节点）；
    • 它可以用来模拟引力（吸引力），只需设置的 strength 参数为正数；
    • 它也可用来模拟电荷力（排斥力），只需设置的 strength 参数为负数；
    • 实现算法使用了the Barnes–Hut approximation（通过将平面不断递归地划分成四个小区域来构建一棵四叉树） 来提高性能；

    方向力(Positioning)
    方向力分为 X 方向和 Y 方向，即将作用力限制在一个维度上（ X 维度或者 Y 维度）