原文地址：https://segmentfault.com/a/1190000039054038

前言

可视化是一种利用计算机图形学和图像处理技术，将数据转换成图形或图像在屏幕上显示出来，再进行交互处理的理论、方法和技术。数据在经过图可视化的方式展示后能够辅助用户去分析复杂的关系数据，从而发现数据中蕴含的价值。而图布局则是图可视化中非常重要的基石，对可视化图进行合理的布局可以帮助我们快速分析，准确定位问题。如果没有对图进行合理的布局，那么用户就很难从图中提炼出想要的信息，甚至有时候还会误导用户作出错误的判断。例如在下图中，左侧是没有进行过特定布局杂乱无章的图，右侧则是经过有向分层布局后的图，我们从右图中可以非常快速地分辨出图中的根节点、二级节点、三级节点以及节点之间的关系等重要信息，但是我们却很难从左侧图中识别出这些信息。因此在我们日常的业务场景使用合理的图布局至关重要。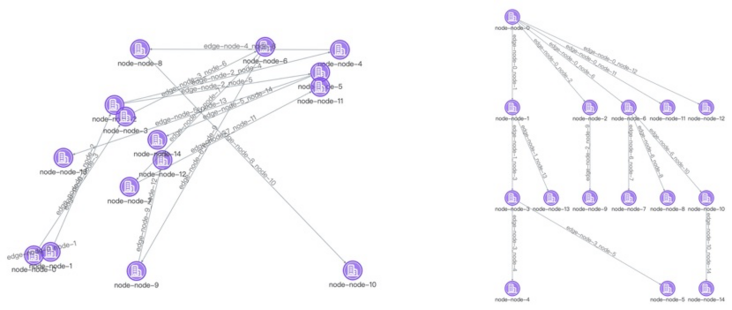
image.png

常见的布局方案

各类布局图

在可视化领域中常见的布局有树形布局、Dagre 布局、力导布局、同心圆布局、网格布局等。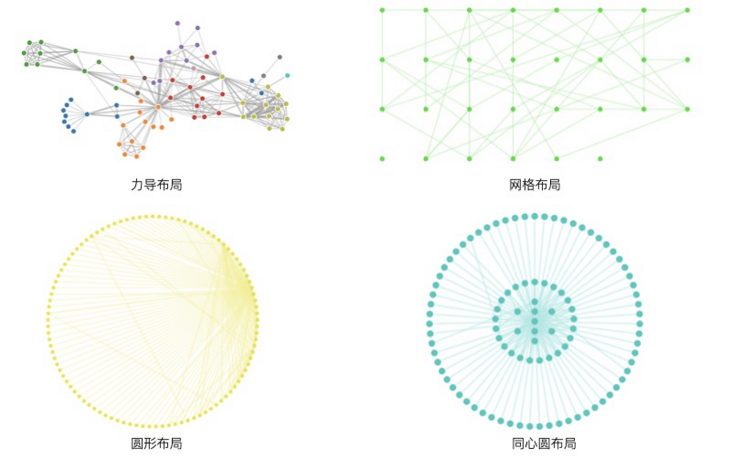
image.pngimage.png

各类布局方案以及对应的场景

布局方案 适用场景
力导布局 适用于描述事物间关系，比如社交网络关系、计算机网络关系、资金交易关系等各类关系网络场景
网格布局 节点按一定排序网状排开，适应于分层网络，便于看清整体层次
同心圆布局 将节点按照度数排序，节点度数大的一群点会排列在最中心，度数小的节点会分布在最外层，使其以同心圆的方式排布，适应于快速查找出度数较多的节点
圆形布局 适用于查找关联关系较多的关键节点场景，例如在圆形布局的图中可以明显分辨出哪些节点关联关系较多
树形布局 / Dagre布局 适应于层次分明，或者需要严密拓扑性质的场景，比如分层网络图、流程图等

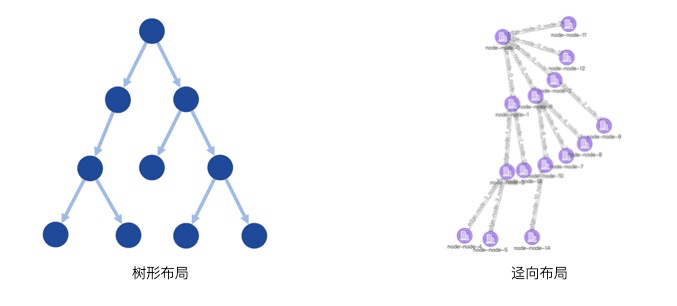
树形布局

在很多业务场景中，我们通常会比较关注节点之间的层级关系，并且还需要判断图中是否存在环路等情况情况，这种情况下树形布局就非常合适，对于树形布局大家常规的认识肯定是下图左侧这种传统的布局形式，从根节点出发，按照层级关系向同一方向自上而下或自左而右累加。这种展示方式最为直观，也符合我们对树的常规感知，但它也存在一些问题，比如对屏幕空间的利用率不高。越靠近根节点的层级节点越稀疏，导致大量留白，从而浪费屏幕空间。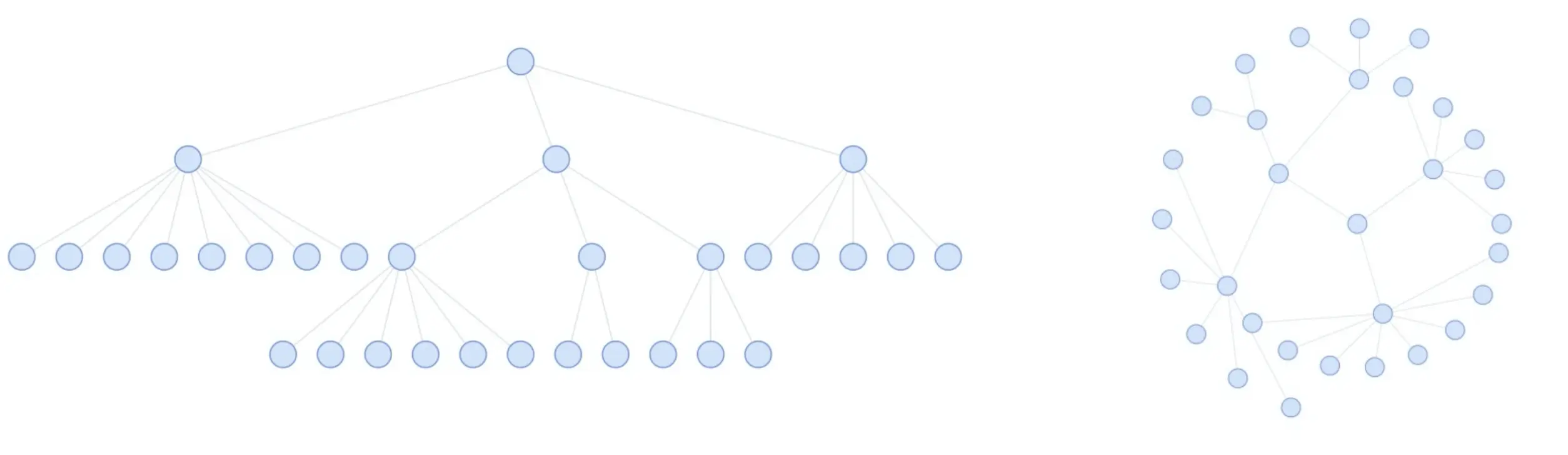
image.png
因此对于一些布局空间有限的场景，我们可以采用上图（右）的布局方式，该布局是根据节点深度将整棵树以辐射状展示，根节点在最中心，叶子节点在外围。这种布局方式相比于传统的树图布局能够以更好地利用空间，美中不足之处就是可能不如传统树图布局符合人对树结构的感知，并且随着节点数量的增加，树的路径就越不清晰，不过我们也可以通过一定的交互方式来弥补不足，比如点击某个子节点默认展示该节点的回溯路径。

树形布局的算法难度不大，我在 GitHub 上找了一篇关于紧凑树布局的文章，大家可以点击直达，这文章对于实现的原理也有详细的阐述，本文就不再讲述了。

Dagre 布局

Dagre（有向无环图）布局其实有点类似于树形布局，不过也有些差异；对于任何有向树图必定是有向无环图，但是有向无环图未必是有向树图，由于有向无环图有其严密的拓扑性质，使其具有很强的流程表达能力。基于这一特点，在很多需要对零散化任务进行组织和控制的场景中，应用非常广泛，比如下图是阿里云的机器学习平台 PAI 中的截图，它就是一张典型的有向无环图。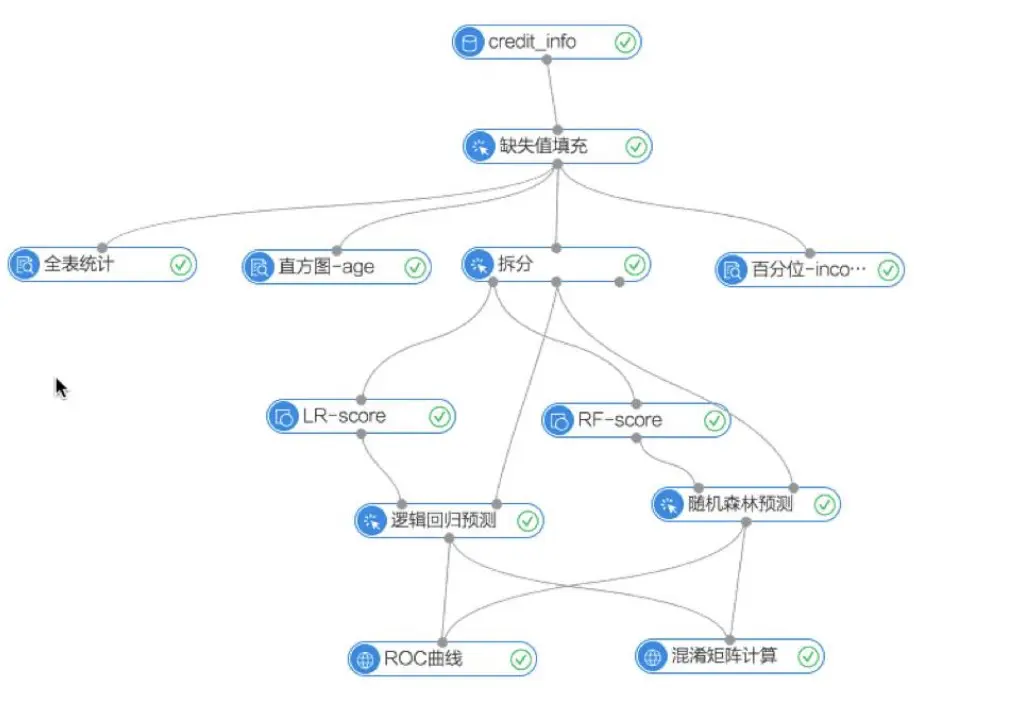
image.png
对于 DAG 布局 GitHub 上有一套成熟的算法传送门，很多可视化库的 DAG 布局也都借鉴了该方案，从下面的 runLayout 函数我们可以大致看出 dagre 布局的过程。

  1. function runLayout(g, time) {
  2.   time("    makeSpaceForEdgeLabels", function() { makeSpaceForEdgeLabels(g); });
  3.   time("    removeSelfEdges",        function() { removeSelfEdges(g); });
  4.   time("    acyclic",                function() { acyclic.run(g); });
  5.   time("    nestingGraph.run",       function() { nestingGraph.run(g); });
  6.   time("    rank",                   function() { rank(util.asNonCompoundGraph(g)); });
  7.   time("    injectEdgeLabelProxies", function() { injectEdgeLabelProxies(g); });
  8.   time("    removeEmptyRanks",       function() { removeEmptyRanks(g); });
  9.   time("    nestingGraph.cleanup",   function() { nestingGraph.cleanup(g); });
  10.   time("    normalizeRanks",         function() { normalizeRanks(g); });
  11.   time("    assignRankMinMax",       function() { assignRankMinMax(g); });
  12.   time("    removeEdgeLabelProxies", function() { removeEdgeLabelProxies(g); });
  13.   time("    normalize.run",          function() { normalize.run(g); });
  14.   time("    parentDummyChains",      function() { parentDummyChains(g); });
  15.   time("    addBorderSegments",      function() { addBorderSegments(g); });
  16.   time("    order",                  function() { order(g); });
  17.   time("    insertSelfEdges",        function() { insertSelfEdges(g); });
  18.   time("    adjustCoordinateSystem", function() { coordinateSystem.adjust(g); });
  19.   time("    position",               function() { position(g); });
  20.   time("    positionSelfEdges",      function() { positionSelfEdges(g); });
  21.   time("    removeBorderNodes",      function() { removeBorderNodes(g); });
  22.   time("    normalize.undo",         function() { normalize.undo(g); });
  23.   time("    fixupEdgeLabelCoords",   function() { fixupEdgeLabelCoords(g); });
  24.   time("    undoCoordinateSystem",   function() { coordinateSystem.undo(g); });
  25.   time("    translateGraph",         function() { translateGraph(g); });
  26.   time("    assignNodeIntersects",   function() { assignNodeIntersects(g); });
  27.   time("    reversePoints",          function() { reversePointsForReversedEdges(g); });
  28.   time("    acyclic.undo",           function() { acyclic.undo(g); });
  29. }

如果我们按每个 time 相当于每步的计算过程来算，emm… 这样算下来应该是有 26 个步骤，这也太复杂了吧？不过深入去看了下调用的各个函数，就会发现实际上大部分函数其实都是在处理数据。DAG布局的核心步骤应该可以大致分为 4 步：

  1. 去除环，包括自环和非自环即 removeSelfEdges 和 makeSpaceForEdgeLabels （最后如果有自环路还是会回填回去的）
  2. 划分层级即 nestingGraph.run
  3. 同层级内节点排序即 addBorderSegments

  4. 计算位置布局

    力导布局

    了解关系图谱相关业务的同学肯定对力导布局不陌生，力导布局最早是被 Eades 提出的，之后被很多研究人员重新定义和改进，下图是 D3 上的三种力导布局。
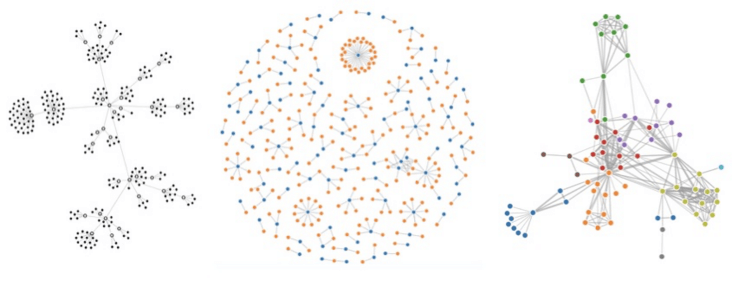
    image.png
    力导布局的优势在于由于互斥力的存在，可以减少节点之间的重叠，但实际上当节点过多时，仍然会出现节点重叠的情况，在有限的空间里想要避免所有节点不重叠，这已被证明是一个 NP 难题（世界难题，目前无解），并且在一些大数据的场景下还会出现毛团现象，如下图。
    image.png

    圆形布局

    圆形布局是将所有节点先进行一定的排序（这里的排序可以自定义），然后再按序排列在一个圆环上，这种布局的好处是通过自定义排序后的圆形布局，我们可以快速分析出想要的结果，例如下图是按照关联度数排序后的圆形布局，我们可以很清晰地看出红框的中的节点相较于其他节点的关联度数更多，这是其他布局方式所难以达到的效果，比如使用上文的力导布局，就很难分辨出哪些节点的关联度数更多。但是它的缺点也比较明显，因为随着节点数量的增加，圆环的半径也会越来越大，很容易就超出我们常规屏幕的可视区域。
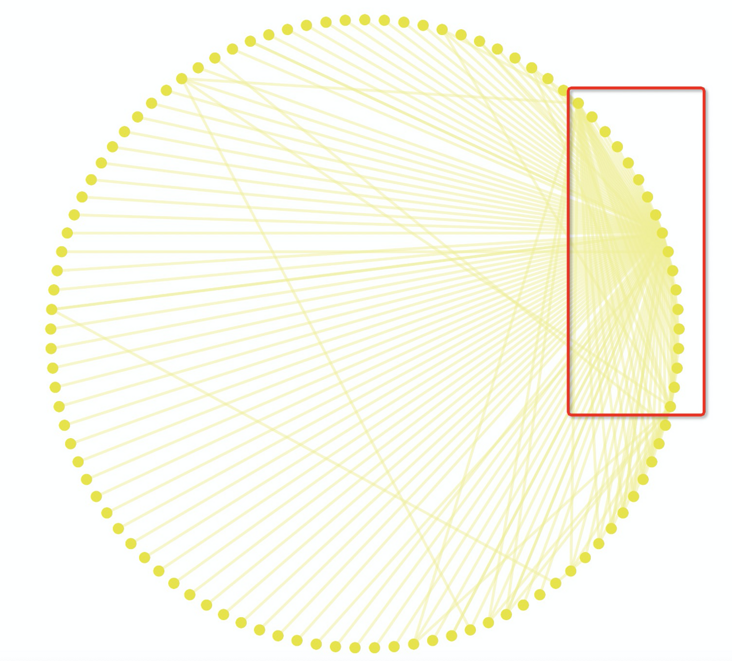
    image.png
    关于圆形布局的具体方式，实际上核心步骤实际就只有两步：

  5. 自定义排序

  6. 环形布局

关于第二步的环形布局，这个算法就比较固定了，主要是根据节点的数量计算出每个节点在环形中的位置即可，下面是 antvis/layout 中关于环形布局的代码：

  1. public execute() {
  2.     const self = this
  3.     const nodes = self.nodes
  4.     const edges = self.edges
  5.     const n = nodes.length
  6.     if (n === 0) {
  7.       if (self.onLayoutEnd) self.onLayoutEnd()
  8.       return
  9.     }
  11.     if (!self.width && typeof window !== 'undefined') {
  12.       self.width = window.innerWidth
  13.     }
  14.     if (!self.height && typeof window !== 'undefined') {
  15.       self.height = window.innerHeight
  16.     }
  17.     if (!self.center) {
  18.       self.center = [self.width / 2, self.height / 2]
  19.     }
  20.     const center = self.center
  22.     if (n === 1) {
  23.       nodes[0].x = center[0]
  24.       nodes[0].y = center[1]
  25.       if (self.onLayoutEnd) self.onLayoutEnd()
  26.       return
  27.     }
  29.     let radius = self.radius
  30.     let startRadius = self.startRadius
  31.     let endRadius = self.endRadius
  32.     const divisions = self.divisions
  33.     const startAngle = self.startAngle
  34.     const endAngle = self.endAngle
  35.     const angleStep = (endAngle - startAngle) / n
  36.     // layout
  37.     const nodeMap: IndexMap = {}
  38.     nodes.forEach((node, i) => {
  39.       nodeMap[node.id] = i
  40.     })
  41.     self.nodeMap = nodeMap
  42.     const degrees = getDegree(nodes.length, nodeMap, edges)
  43.     self.degrees = degrees
  44.     if (!radius && !startRadius && !endRadius) {
  45.       radius = self.height > self.width ? self.width / 2 : self.height / 2
  46.     } else if (!startRadius && endRadius) {
  47.       startRadius = endRadius
  48.     } else if (startRadius && !endRadius) {
  49.       endRadius = startRadius
  50.     }
  51.     const angleRatio = self.angleRatio
  52.     const astep = angleStep * angleRatio
  54.     const ordering = self.ordering
  55.     let layoutNodes = []
  56.     if (ordering === 'topology') {
  57.       // layout according to the topology
  58.       layoutNodes = self.topologyOrdering()
  59.     } else if (ordering === 'topology-directed') {
  60.       // layout according to the topology
  61.       layoutNodes = self.topologyOrdering(true)
  62.     } else if (ordering === 'degree') {
  63.       // layout according to the descent order of degrees
  64.       layoutNodes = self.degreeOrdering()
  65.     } else {
  66.       // layout according to the original order in the data.nodes
  67.       layoutNodes = nodes
  68.     }
  70.     const clockwise = self.clockwise
  71.     const divN = Math.ceil(n / divisions) // node number in each division
  72.     for (let i = 0; i < n; ++i) {
  73.       let r = radius
  74.       if (!r && startRadius !== null && endRadius !== null) {
  75.         r = startRadius + (i * (endRadius - startRadius)) / (n - 1)
  76.       }
  77.       if (!r) {
  78.         r = 10 + (i * 100) / (n - 1)
  79.       }
  80.       let angle =
  81.         startAngle +
  82.         (i % divN) * astep +
  83.         ((2 * Math.PI) / divisions) * Math.floor(i / divN)
  84.       if (!clockwise) {
  85.         angle =
  86.           endAngle -
  87.           (i % divN) * astep -
  88.           ((2 * Math.PI) / divisions) * Math.floor(i / divN)
  89.       }
  90.       layoutNodes[i].x = center[0] + Math.cos(angle) * r
  91.       layoutNodes[i].y = center[1] + Math.sin(angle) * r
  92.       layoutNodes[i].weight = degrees[i]
  93.     }
  95.     if (self.onLayoutEnd) self.onLayoutEnd()
  97.     return {
  98.       nodes: layoutNodes,
  99.       edges: this.edges,
  100.     }
  101.   }

但是关于第一步的自定义排序，由于排序算法的不确定，因此会让我们的环形布局出现很多很有意思的布局情况。也有相关研究人员专门研究过此类布局，论文详情大家可以点击直达。

同心圆布局

同心圆布局在图分析的场景中通常是将节点先按照度数排序，度数最大的节点会排列在最中心的位置，越往外度数越小，整体成同心圆形式排列，如下图所示。在上文中的圆形布局中，其实我们还是很难精确定位出度数最多的节点，但是同心圆布局可以做到，因为最近接近圆心位置的节点就是度数最多的节点，并且在相同面积下同心圆布局可以比圆形布局容纳更多的节点。因此在查找度数最多节点的场景中，同心圆布局要比圆形布局更占优势。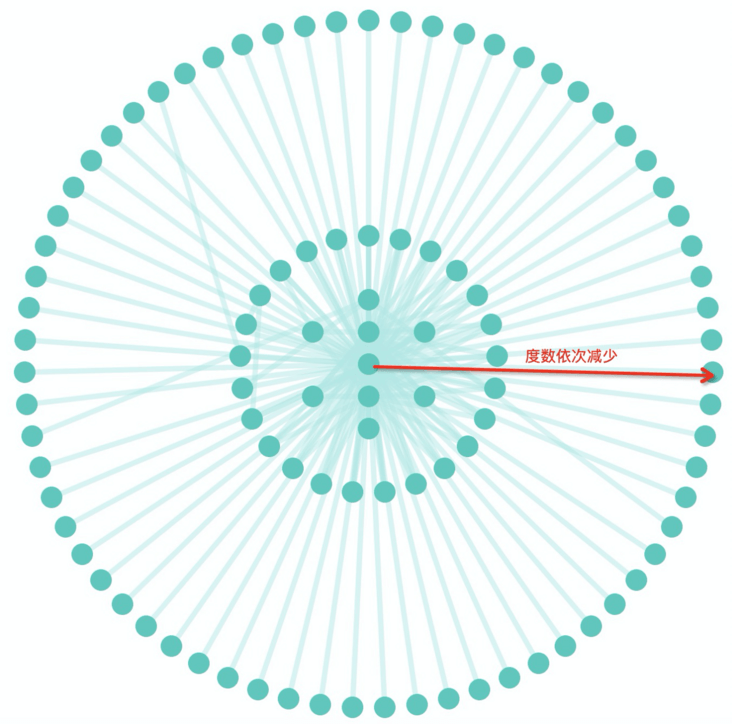
image.png

增量布局

增量布局是为了解决在数据发生增量变化时，使原有布局能够保持相对稳定的问题。在图分析中的关系扩散、关系发现等场景下，分析的数据往往都在持续变化，难以一次性分析完毕。这时就需要增量布局算法，在数据发生变化时能够保持整体布局的相对稳定如下图所示。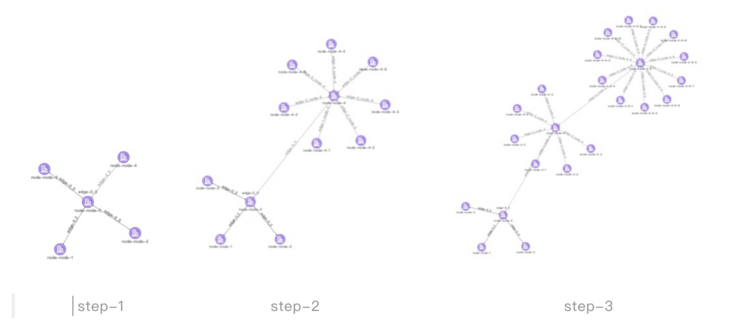
image.png

增量布局一般分为两种情况，一种是稳定布局的增量，一种是力导布局的增量。
• 稳定性布局的增量布局：例如circle，grid布局，新增的节点通过原有的布局函数，节点位置可预测，通过节点的补间动画即可完成
• 力导布局的增量布局：如果当前画布是力导布局，新增节点通过tweak算法，为新增节点找到合适的初始位置，再通过力导的能量优化，完成整体布局，具体的细节图如下。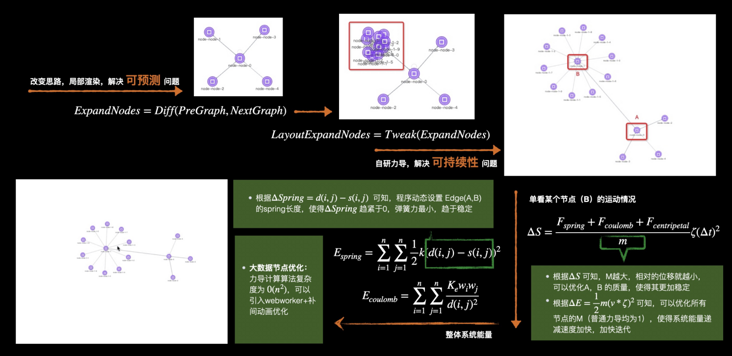
image.png

子图布局

子图的概念源于图论，它是指节点集和边集分别是某一图的节点集的子集和边集的子集的图。若这个节点子集或边子集是真子集，则称这个子图为真子图；若图G的每一个节点也是它的子图H的节点，则称H是G的支撑子图。设S是V(G)的子集，以S为节点集，以G的所有那些两端点都在S内的边组成边集，所得到的G的子图称为S在G中的导出子图。设B是E(G)的子集，由G的所有与B内至少有一条边关联的节点组成节点集，以B为边集，所得到的G的子图称为B在G中的边导出子图；对于某种性质P，若一个图的具有P的子图不是任何具有P的子图的真子图，则称它为具有P的极大子图，在所有极大子图中，边数最多的那个称为最大子图。

上文讲了一大段，估计大家对于子图还是没有任何体感。不过我们来看下图，可能就会很快理解子图布局了。由于在真实的业务场景中，我们的数据关系经常会是错综复杂的，因此我们很难只用一种布局方式就能清晰地表达，上文我们也讲到了各类布局方式的优势和劣势，那么我们是否可以将各类布局方案的优势融合在一起，呈现出更合理的布局效果，子图布局就是为了解决此类问题。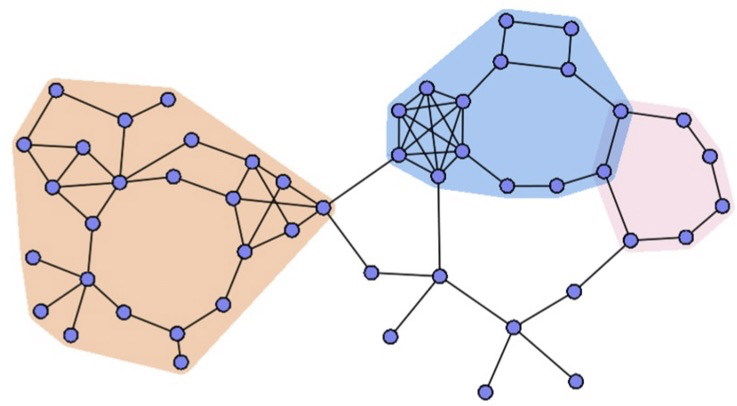
image.png
上图的布局方式即把子图布局的数据单独出来，分别施加布局算法，得到一个准确的位置，然后统一渲染到画布上。不过，这里面存在两个技术难点：

  1. A，B 两组数据点，初始位置如何确定？
  2. A，B 两组数据如果存在关联点，它们将会对两个子网络产生何种影响？

这个其实可以提供一些策略，比如两组数据的初始位置，可以通过A，B组数据的平均中心点来确定。而A，B组见相关联的共同点可以通过一些数学计算，得出一个合适的组内边缘位置。

智能布局

针对子图布局存在的技术难点，有些研究方向也尝试通过机器学习建模的方式，使用大量的标注数据（标记布局分类）进行模型训练，在真实的业务场景中通过模型对真实的图数据的布局方式进行预测，从而推荐出该数据最适合的布局，具体过程如下图。
image.png

下图是北大可视化研究人员关于智能布局的研究，他们提出了一个基于拉普拉斯变换的图布局保持算法。该工作能自动生成初始图布局，允许用户在图中任意选取子图并进行个性化编辑。收集多用户编辑的子图，对这些子图进行合理的缩放，保存子图中任意两点间的距离，结合图的初始布局运用拉普拉斯子图保持算法得到结合了多用户输入的更满足用户需求、易于理解的图布局。如下图所示，用户定义了许多形状各异的子图，该算法可以有效的解决子图编辑冲突，以及将编辑过的子图布局融入到初始布局中，衔接处流畅自然，而且子图布局保持效果非常好。图中数字表示经过算法融合后的子图布局与用户输入的子图布局的相似度，完全一样为100%；有兴趣的同学可以点击直达。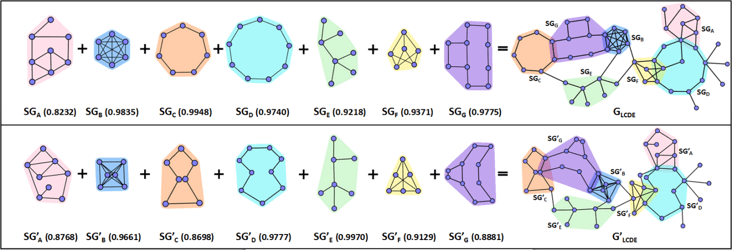
image.png

图分析中的布局

上文说了那么多的布局方案，下面我们就来看看真实图分析中的案例吧。下图就是我们在业务中经常可能会看到的场景，这是常规的力导布局，节点之间都没有任何重叠，所以整体看起来整张图的关系网络还是比较清晰的，并且我们还可以通过点击某个节点高亮其所有一度关系的交互来查看每个节点的关系。我们这次分析的目的是要找出关联度数最多的节点，因为在很多弱社交关系的场景，某类节点关系复杂，往往就意味着风险。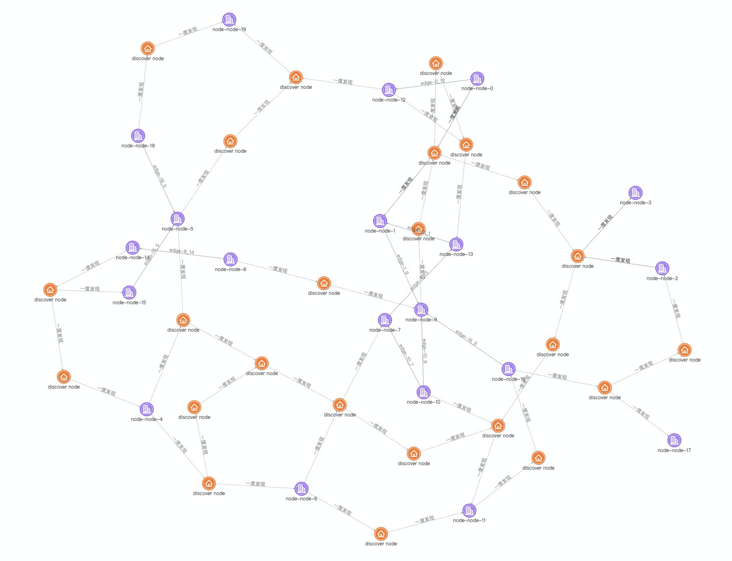
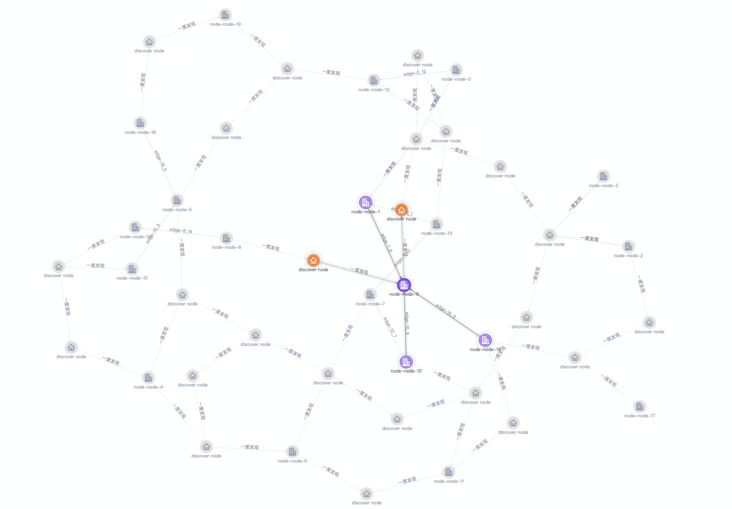
image.pngimage.png
上面的力导布局显然很难帮助我们找出度数最多的节点，除非我们一个节接一个节点地点击用肉眼去统计，但是这显然不太现实。

力导布局 pass，那我来尝试一下树形布局，首先切换到常规的树形布局（又称有向分层布局）就变成下图左侧的样子了，这布局方式也太长了，我是缩到了很小才能勉强看清整张图的全貌，我们再切换到类似辐射型的树形布局方式如右侧所示，这时候不用缩小我们就能看清整张图的全貌了，而且节点的层次也非常清晰明了，尽管如此，我们找的度数最大的节点还是很难分辨出来。
image.png
树形布局 pass，那我们再切换成圆形布局试试，上文说到圆形布局一般都是先自定义排序后再布局的，这次我们的目标是要找出度数最多的节点，那我果断就选择了按度数排序的方式，最终的结果是下图左侧这样子。emm… 好像有点不太对，我还是没法一眼看出关联度数最多的节点，我尝试点击下布局中右侧的几个节点，因为圆形布局中的节点是按照度数排序后的，从图中可以看出右上部分的节点度数较稀疏，有呈逆时针增减增加的趋势，所以只要在图中的右侧找出某个节点的度数比相邻的节点大，那么这个节点就是度数最大的节点，如下图右侧就是我找出的度数最大的节点，但是实际上度数最大的节点也有可能存在多个，因此通过圆形的布局去查找度数最大的节点也不是非常完美。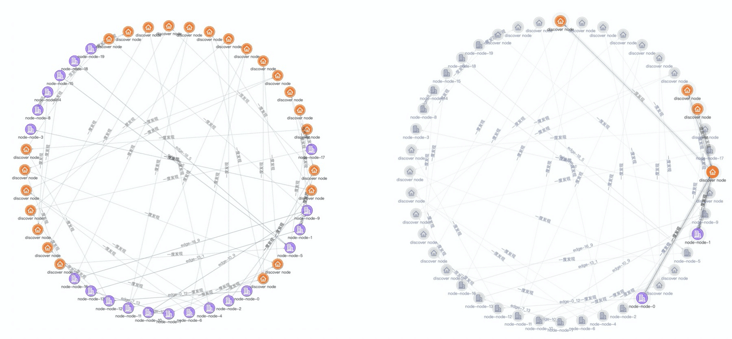
image.png
那我们在尝试一下同心圆布局，因为同心圆布局可以将度数最大的节点放置最接近圆心的位置，理论上来说对于找出度数最大的节点，堪称完美。下图就是同心圆布局的最终效果，不出所料，这种布局对于定位节点度数真的是非常完美，从中我们快速定位到度数最大的节点，并且每个节点的度数也都清晰明了。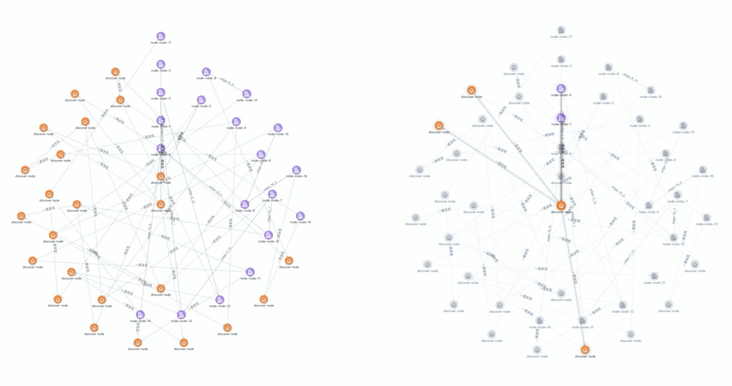
image.png

总结

不同的业务场景，应该选择什么样的布局才是合理的？本文主要探讨了各种不同场景的布局解决方案，希望能给大家在图布局方面提供一定的思路和参考。