这篇文章是承接上一篇文章《 层次数据可视化》,这两篇文章分别对应图可视化中的2大类: 层次数据的可视化和网络数据的可视化,本篇主要介绍网络数据可视化。
不具备层次结构的数据可统称为网络(network)数据,通常用图(Graph)表示。 图是由顶点集V和顶点间的关系集合E(边的集合)组成的一种数据结构,可以用二元组定义为:G =(V, E)。
1. 网络数据的布局**
1.1 节点-链接法
用节点表示对象,边表示关系。显式地表达事物之间的关系,能帮助人们快速建立事物之间的联系。
实用性和美观性原则如下:
- 尽量避免边交叉。
- 节点和边尽量均匀分布。
- 边的长度与权重相关。
- 可视化效果整体对称。
- 网络中相似的子结构的可视化效果相似。
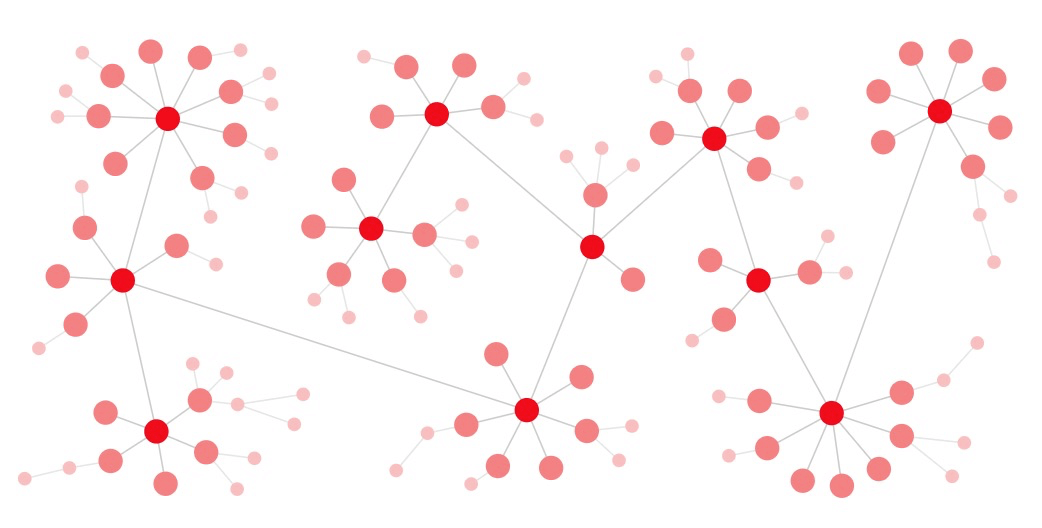
1.1.1 力引导布局
优点:易于理解,容易实现,实现的效果具有较好的对称性和局部聚合性,因此比较美观。且用户可以看到整个布局逐渐趋于动态平衡的过程,使得整个布局结果更容易被接受。
缺点:力引导布局只能达到布局优化,不能达到全局优化。
1.1.2 弧长链接图(arc-diagram)
node-link方法的变种,采用一维布局方式,节点沿某个线性轴或环状排列,圆弧表达节点之间的链接关系。
优点:不能清晰直观地表达图的全局结构。
缺点:节点良好排序后可清晰地呈现环或桥的结构。
ps: 对节点的排序优化问题又称为序列化(serialization)。
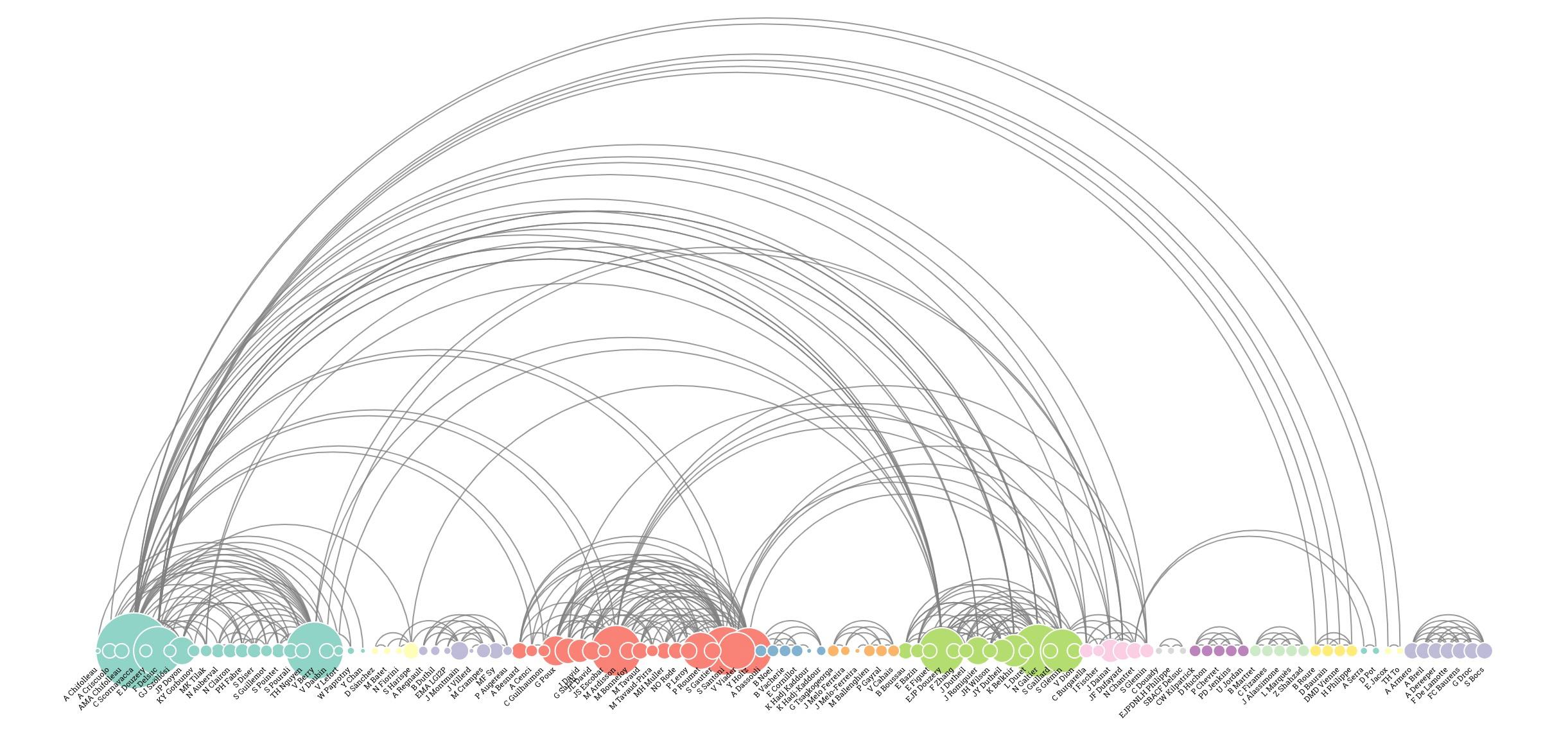
arc-diagram
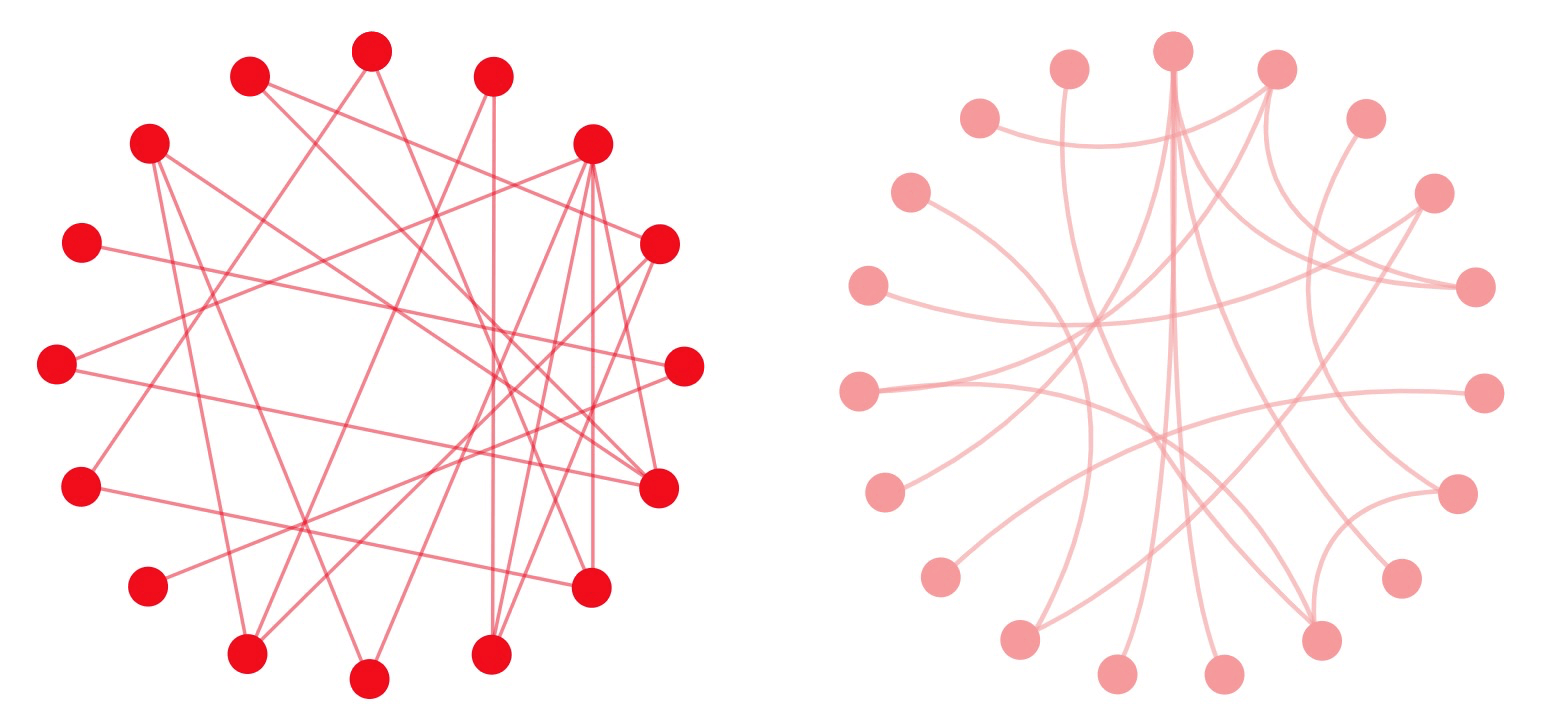
1.1.3 弦图( Chord dragram)
arc-diagram的变体,节点围绕着圆周分布,点与点之间以弧线或贝塞尔曲线连接来表示关系,然后再给每个连接分配数值(通过每个圆弧的大小比例表示)。用颜色将数据分成不同类别,有助于进行比较和区分。
优点:非常适合用来比较数据集或不同数据组之间的相似性。
缺点:需要显示的连接较多时,比较混乱。
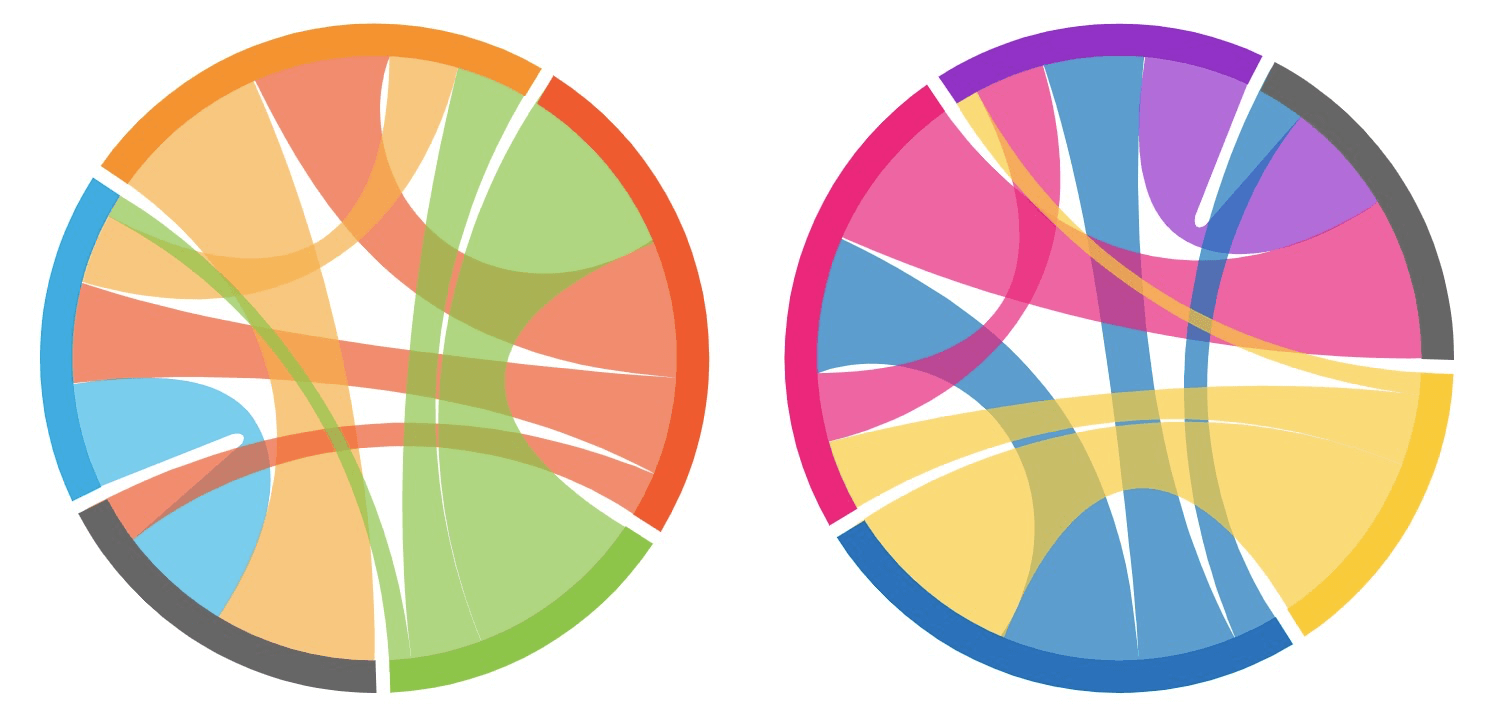
chord dragram
**
弦图的一个变体:仅显示节点和连接线,强调数据之间的连接关系。
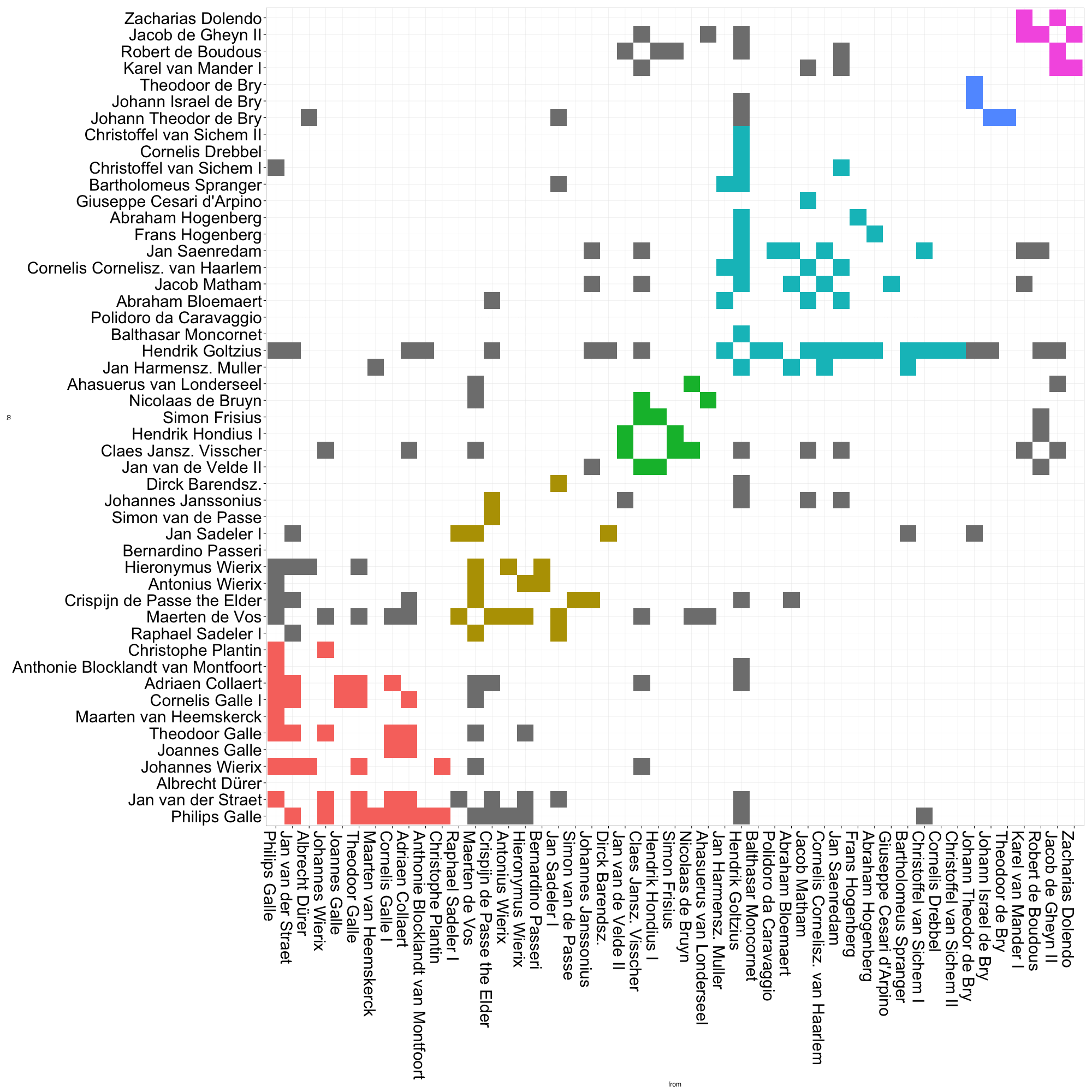
1.2 邻接矩阵(Adjacency Matrix)
矩阵内点的位置(i, j)表示第i个节点和第j个节点之间的关系。
优点:能很好地表达完全图,可显著表达节点之间的直接关系。能完全规避边的交叉问题。
缺点:**不能呈现网络的拓扑结构,不能明显表达关系的传递性。
2. 图可视化中的交互
2.1 基于视点的交互
指用交互手段来预测和帮助用户在图中切换视点。
- 常规方法: 平移、缩放、旋转等
- Link sliding
- Bring & Go
2.2 基于图元的交互
指对于一个可视化映射元素的交互。
- 如节点的选择、高亮、删除、移动、展开和收缩。
2.3 基于图结构的交互
基于图结构的交互是一种宏观结构的交互手段,核心思想是“焦点+上下文”(focus + context)技术。
- 鱼眼技术(fisheye)及其变种。
3. 其他
3.1 GMap
将网络图用地图形式表达的方法,将数据与数据的分类表示成地图的形式,可以让人更容易理解数据的集合关系。
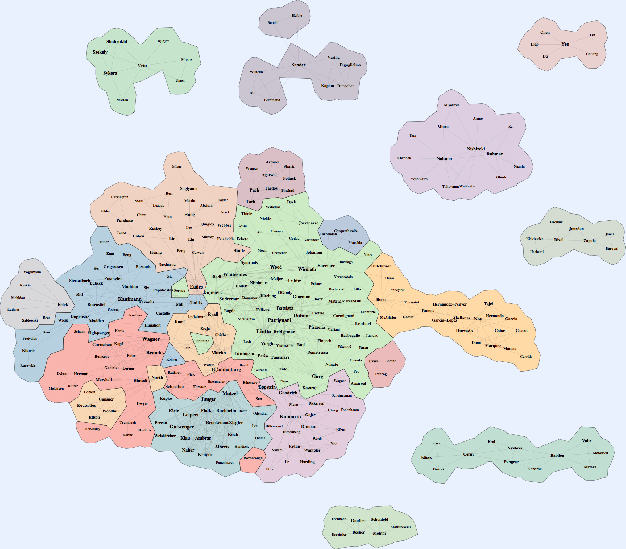
1994~2004年之间参加graph drawing会议的学者之间的合著关系
3.2 动态网络数据可视化
“动态”可以理解为节点的增减、关系的增减、节点/关系权重的变化这三种。如果完全对动态网络数据逐帧进行重新布局,则会导致视觉连续性的缺失。动态网络布数据可视化的目标是尽量保持帧间连续性和一致性。这也是目前网络数据可视化的一大挑战。