什么是矩形树图？

矩形树图由马里兰大学教授Ben Shneiderman于上个世纪90年代提出，适合展示具有层级关系的数据，能够直观的体现同级之间的比较。从根节点开始，屏幕空间根据子节点数目被分为多个矩形，矩形面积对应节点的权重。每个矩形又按照相应节点的子节点递归进行分割，直到叶节点为止。

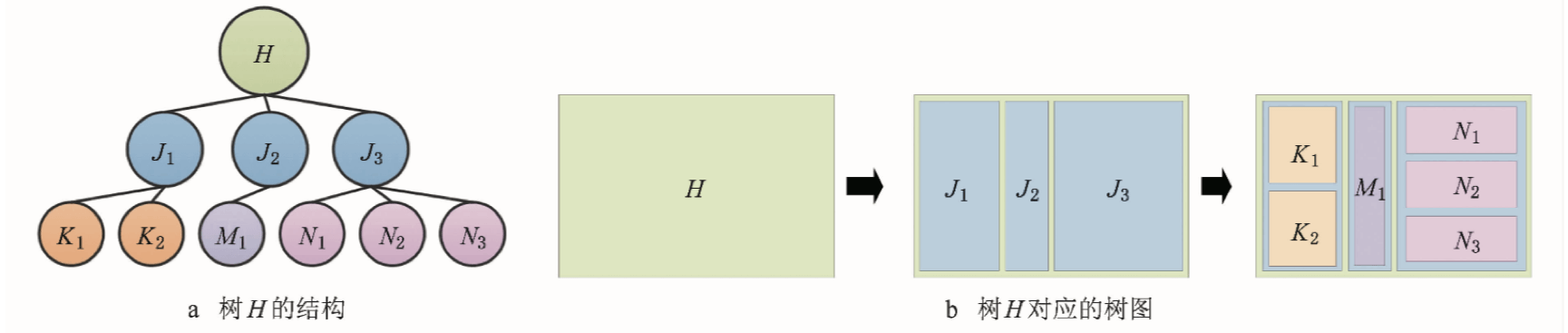
D3矩形树图布局算法研究 - 图1
树到树图映射过程

D3中的矩形树图

我们熟知的AntV的矩形树图也是基于D3的treemap布局。D3提供了6种Tiling算法，分别为：treemapBinary、treemapDice、treemapSlice、treemapSliceDice、treemapSquarify和treemapResquarify。
例如，一个数据结构如下的树图：

  1. {
  2.   name: 'root',    
  3.   children: [{
  4.     name: '分类 1',
  5.     value: 2
  6.   }, {
  7.     name: '分类 2',
  8.     value: 10
  9.   }, {
  10.     name: '分类 3',
  11.     value: 4
  12.   }, {
  13.     name: '分类 4',
  14.     value: 3
  15.   }, {
  16.     name: '分类 5',
  17.     value: 7
  18.   }, {
  19.     name: '分类 6',
  20.     value: 5
  21.   }, {
  22.     name: '分类 7',
  23.     value: 9
  24.   }, {
  25.     name: '分类 8',
  26.     value: 8
  27.   }, {
  28.     name: '分类 9',
  29.     value: 1
  30.   }, {
  31.     name: '分类 10',
  32.     value: 6
  33.   }]
  34. };

6种算法对应的布局图如下所示：
1.正常的顺序绘制
D3矩形树图布局算法研究 - 图2
2.倒序绘制
D3矩形树图布局算法研究 - 图3

几种常见的布局算法

1. Slice-and-dice

Slice-and-dice是由Johnson等人于1991年提出的，该算法从左至右或自上而下地对矩形进行填充，填充时只考虑子节点顺序和权值所代表的面积。如图2-4所示，在布局的时候很容易产生细长的矩形，不利于用户视觉辨认和鼠标交互。

2. Squarified算法及改进

Squarified算法使得矩形尽量接近正方形，拥有更好的平均长宽比，从而避免Slice-and-dice算法的缺点。其思想是：
1）将子节点从大到小进行排列；
2）从权值最大的节点开始，按照沿最短边优先开始，紧靠左边或者下边的原则，从左到右或者从下到上开始填充。
3）当填充第i个子节点时，采用同行同列插入或者新建一行/列的方式，对比第1到i-1个矩形的平均长宽比，选择平均长宽比低的填充结果作为第i个子节点的填充方式。
以数据集{3，2，6，4，1，2，6}为例，绘制过程如下图所示。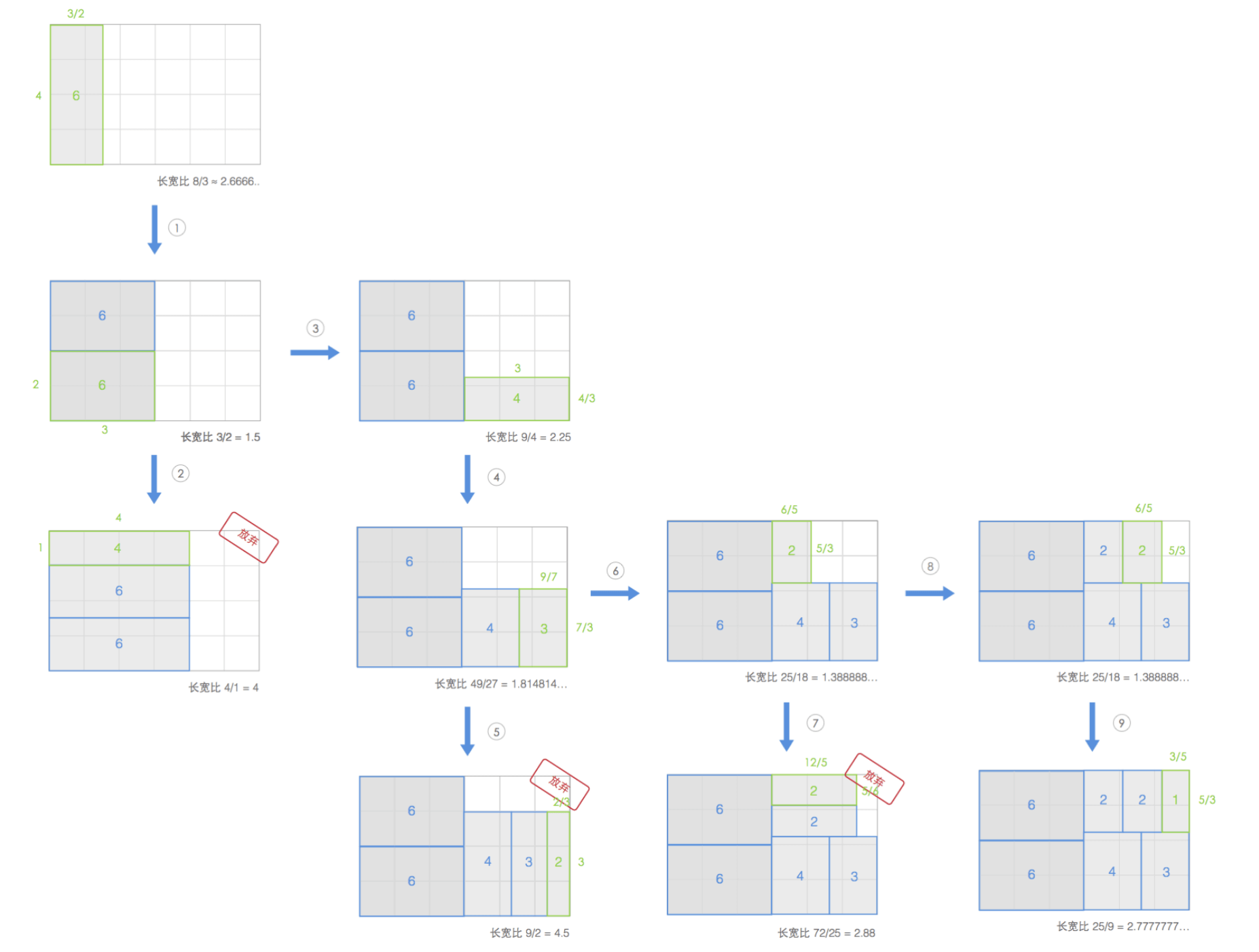
D3矩形树图布局算法研究 - 图4
Squarified算法极大地改善了矩形的长宽比，但缺点是在绘制图形时，打乱了数据原有的顺序，因为对数据集先进行了排序。当权值发生改变时，新旧树图之间会有很大的跳变，视觉效果不连续，因而其稳定性和顺序性较差。针对该问题，Pivot和Strip算法被提出。

Pivot算法

Pivot算法在长宽比和稳定性等方面做了一个折中。算法的主体思想是通过一个Pivot节点Rp，将子节点集分割成3个部分R1，R2和R3。R1由所有节点序号小于Rp的子节点组成，R2内的节点序号必须在Rp之后并且保证布局时Rp能达到接近1的长宽比，剩余的子节点组成R3。然后先对Rp，R1，R2和R3的权值进行布局。布局后对R1，R2和R3的封闭区间在进行矩形划分。重复上述步骤，直到所有同层次的节点全部布局完成。根据Rp的选择，分为3中布局算法，分别是选择中间节点Pivot-by-middle，选择权值最大的子节点Pivot-by-size，选择能将R1和R3两个节点组的权值之和最接近的节点作为Rp Pivot-by-split-size。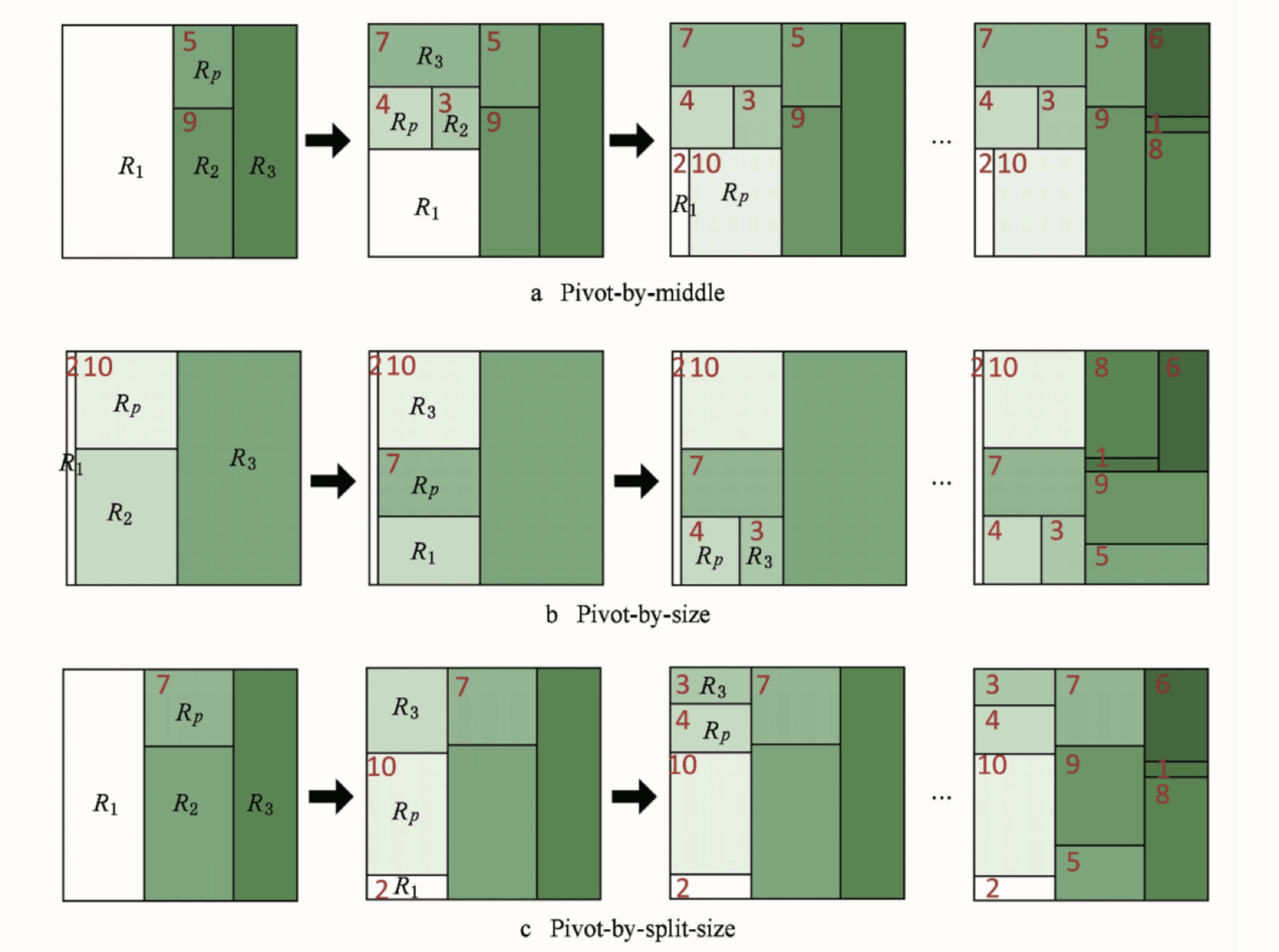
D3矩形树图布局算法研究 - 图5
3种Pivot布局算法的树图生成过程

Strip算法

Pivot算法在保证较好的长宽比的前提下，只能保证节点的部分有序，Strip算法可以进一步提高矩形树图的连续性和稳定性。其基本思想是将子节点按照原始的顺序和Squarified中最优平均长宽比的原则，以紧靠上边或者自左向右的方式填充。其矩形树图的生成过程如下：

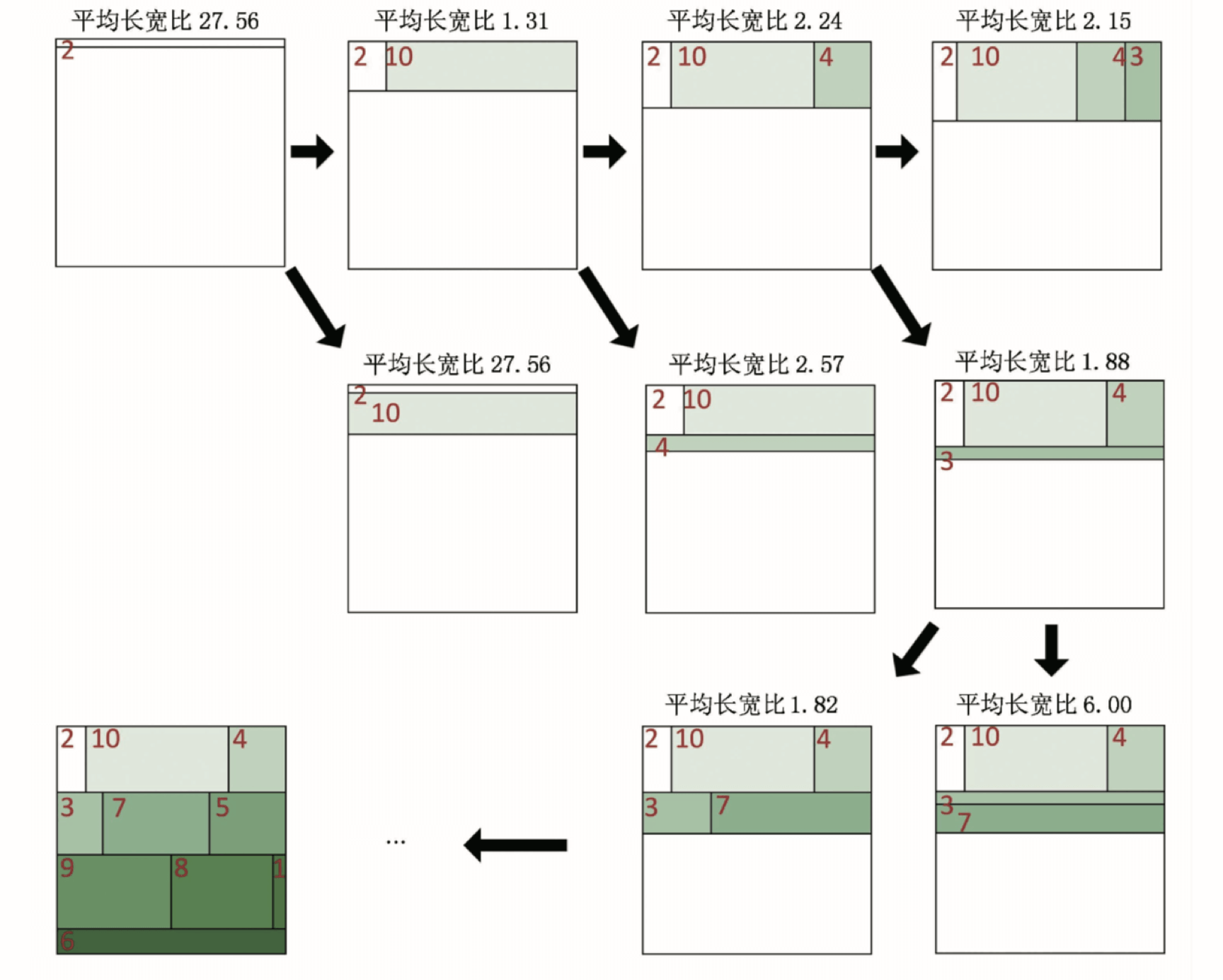
D3矩形树图布局算法研究 - 图6
可以看出，Strip算法在最后一步很容易产生狭长的矩形条，从而影响布局的长宽比和用户交互。

D3的Squarified算法

D3使用的是最基础的没有对数据集进行倒序处理的Squarified算法，默认的长宽比是黄金比例(sqrt(5) + 1) / 2【源码】。对比示例图5在数据集无序和有序的情况下的分割，可以看出数据集的顺序对矩形树图的产生有较大影响，有序的数据集具有更好的长宽比。如果对数据的顺序没有要求的话，建议先对数据集进行排序处理。

3. treemapBinary

D3还提供了利用二叉树来布局的算法，思想是递归地将指定节点划分为近似平衡的二叉树，为宽矩形选择水平分区，为高矩形选择垂直分区的布局方式，效果如图1所示。源码如下：

  1. export default function(parent, x0, y0, x1, y1) {
  2.   var nodes = parent.children,
  3.       i, n = nodes.length,
  4.       sum, sums = new Array(n + 1);
  5.   for (sums[0] = sum = i = 0; i < n; ++i) {
  6.     sums[i + 1] = sum += nodes[i].value;
  7.   }
  8.   partition(0, n, parent.value, x0, y0, x1, y1);
  9.   function partition(i, j, value, x0, y0, x1, y1) {
  10.     if (i >= j - 1) {
  11.       var node = nodes[i];
  12.       node.x0 = x0, node.y0 = y0;
  13.       node.x1 = x1, node.y1 = y1;
  14.       return;
  15.     }
  16.     var valueOffset = sums[i],
  17.         valueTarget = (value / 2) + valueOffset,
  18.         k = i + 1,
  19.         hi = j - 1;
  20.     while (k < hi) {
  21.       var mid = k + hi >>> 1;
  22.       if (sums[mid] < valueTarget) k = mid + 1;
  23.       else hi = mid;
  24.     }
  25.     if ((valueTarget - sums[k - 1]) < (sums[k] - valueTarget) && i + 1 < k) --k;
  26.     var valueLeft = sums[k] - valueOffset,
  27.         valueRight = value - valueLeft;
  28.     if ((x1 - x0) > (y1 - y0)) {
  29.       var xk = (x0 * valueRight + x1 * valueLeft) / value;
  30.       partition(i, k, valueLeft, x0, y0, xk, y1);
  31.       partition(k, j, valueRight, xk, y0, x1, y1);
  32.     } else {
  33.       var yk = (y0 * valueRight + y1 * valueLeft) / value;
  34.       partition(i, k, valueLeft, x0, y0, x1, yk);
  35.       partition(k, j, valueRight, x0, yk, x1, y1);
  36.     }
  37.   }
  38. }

此算法的思想是将节点转化为近似平衡的二叉树。首先将数据集c{2，10，4，3，7，5，9，8，1，6}处理得到合集a{0，2，12，16，19，26，31，40，48，49，55}，其中a[0] = 0， a[i + 1]= c[0] + c[1] + … + c[i]。然后开始找距离[0，55]的中间点27.5最近的点，即26（较低版本源码中是找小于中间点最大值之后的那个点，即31），将区间分成[0，26]和[26, 55]，接着是对区间继续划分，找到距离13最近的点，即12，区间[0，26]被分成[0，12]和[12，26]，以此类推，直到区间被不能再分割。 将每次划分的左右区间的值打印出来，可得到如下的过程：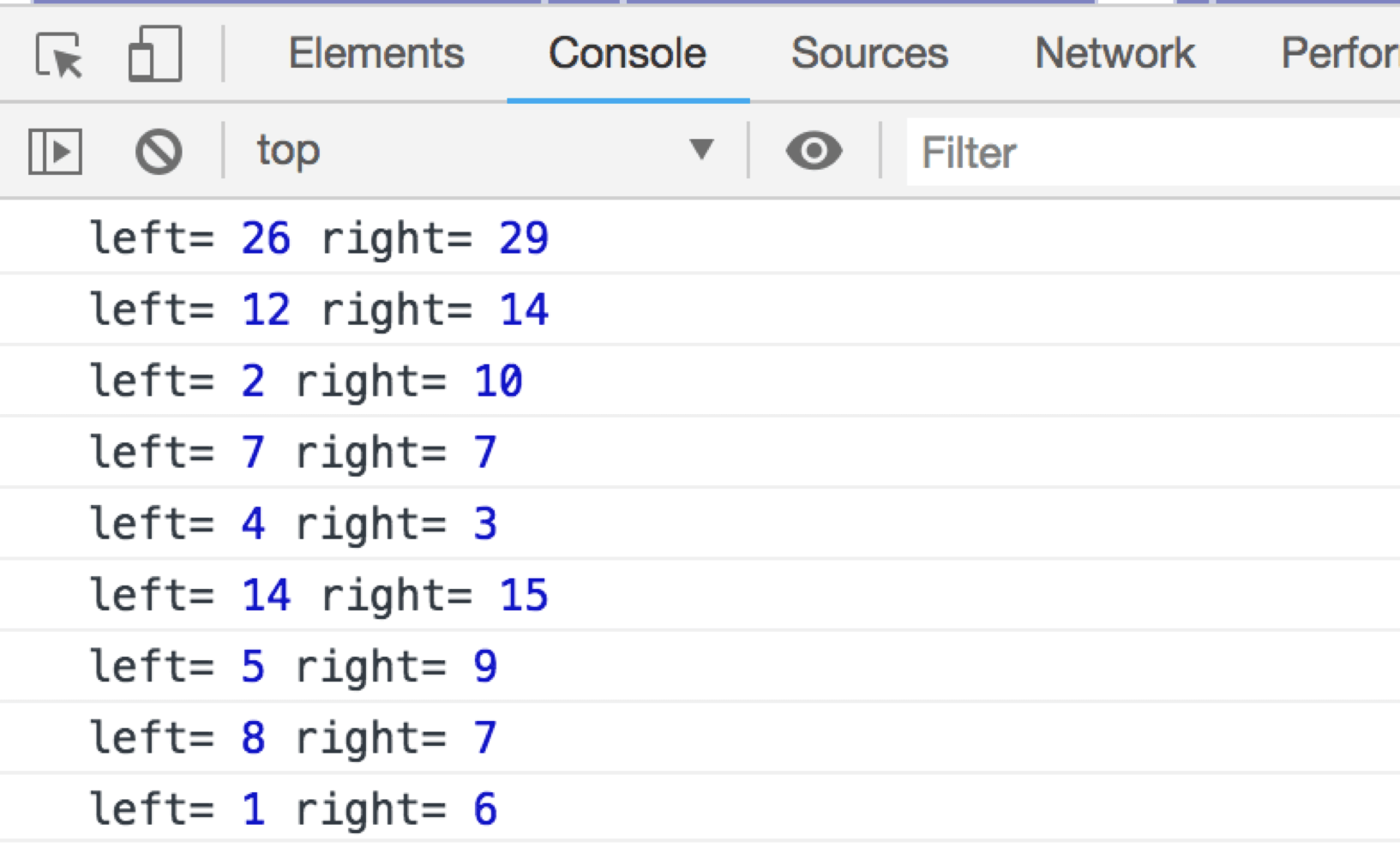
D3矩形树图布局算法研究 - 图7
上述数据集可以转化为如下的二叉树，并完成矩形树图的布局：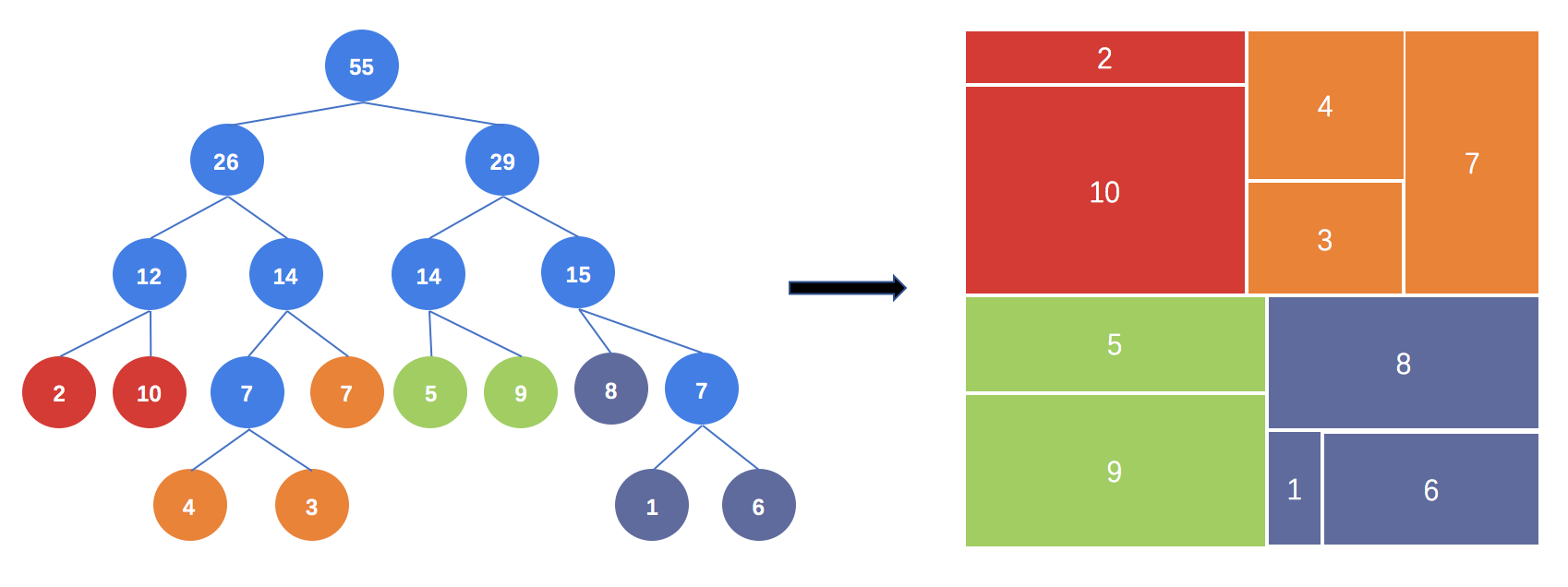
D3矩形树图布局算法研究 - 图8

衡量布局算法的指标

衡量一个布局算法的评价指标只要有平均长宽比、连续性、可读性和稳定性。平均长宽比是指所有子节点的长宽比的平均值，矩形越接近正方形，越有利于鼠标操作和人眼识别。连续性是指数据集中相邻的子节点在树图中是否也相邻的情况。可读性用来衡量用户在查找某一目标的难易程度，可以用视线方向改变的次数来计算。稳定性是指当子节点的权重发生变化时整个树图的变化程度。
D3中的6中Tiling算法其实可以归结为BinaryTree、Slice-and-Dice和Squarify三种基本算法，下面来比较这几种算法在以上几种指标的表现：

平均长宽比 连续性 可读性 稳定性 备注
BinaryTree 良好 优秀 良好 良好
Slice-and-Dice 很差 优秀 优秀 优秀
Squarify 良好 优秀 良好 良好 D3做了一个折中，当数据集本身有序时可以达到更佳的效果

可以发现，Slice-and-Dice在连续性、稳定性和可读性上表现都很优异，但是平均长宽成了致命的问题。BinaryTree算法可以较好的保证每一个指标，但是相比Squarify算法来说在平均长宽比上稍有逊色，并且在不追求数据有序的情况下，使用Squarify算法是非常合适的。因此，D3中默认的布局算法是Squarify算法。

结语

D3的TreeMap算法并不代表了最佳的布局算法，前文中也提到了几种Squarify算法的优化算法，在保证长宽比的同时，尽量提高其他几项指标。可见，目前还没有一种非常完美的布局算法，或者说算法可以考虑更多的因素，比如在遇到极限值的情况下怎么处理。并且，我们外层定义的容器长宽比其实也会影响到矩形树图的展示，如何根据数据集来自动分析出最佳的外层容器的长宽比。
参考资料：
[1] https://antvis.github.io/vis/doc/chart/details/treemap.html
[2] https://github.com/d3/d3-hierarchy#treemap-tiling
[3] https://www.win.tue.nl/~vanwijk/stm.pdf
[4] 张弛,向小雪,张鹏洲.正方化树图布局算法研究与优化[J].计算机工程与应用,2017,53(09):208-212.
[5] 陈谊,胡海云,李志龙.树图布局算法的比较与优化研究[J].计算机辅助设计与图形学学报,2013,25(11):1623-1634.
[6] http://www.cs.williams.edu/~cs135/f16/lectures/lecture.15.pdf